数据结构-二叉树（1）以及前序、中序、后序遍历（python实现）

上篇文章我们介绍了树的概念，今天我们来介绍一种特殊的树——二叉树，二叉树的应用很广，有很多特性。今天我们一一来为大家介绍。

二叉树

顾名思义，二叉树就是只有两个节点的树，两个节点分别为左节点和右节点，特别强调，即使只有一个子节点也要区分它是左节点还是右节点。

常见的二叉树有一般二叉树、完全二叉树、满二叉树、线索二叉树、霍夫曼树、二叉排序树、平衡二叉树、红黑树、B树这么多种类。我们这篇文章中简单介绍一般二叉树、完全二叉树和满二叉树。

一般二叉树

很简单，只要满足子节点数不超过两个的树就是一棵二叉树。长这样：

满二叉树

满二叉树在一般二叉树的基础上要求除了最后一层的节点之外，每一个节点都必须有两个子节点。

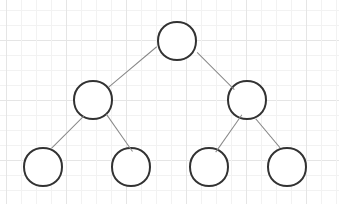
完全二叉树

完全二叉树要求从第一层到倒数第二层组成的树是一颗满二叉树，最后一层的节点要满足从左往右排列。

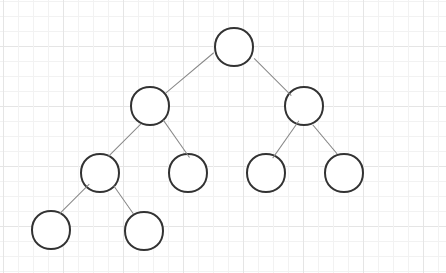
好，关于二叉树的概念，我们就介绍到这里，下面我们来介绍二叉树的前序、中序、后序遍历。

在此之前呢，我们先创建一颗二叉树：

class BinaryTree:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None
    def get(self):
        return self.data
    def getLeft(self):
        return self.left
    def getRight(self):
        return self.right
    def setLeft(self, node):
        self.left = node
    def setRight(self, node):
        self.right = node

好，这里我们定义好了一个二叉树类，并给它添加了一下方法，然后我们来实例化一颗二叉树：

binaryTree = BinaryTree(0)
binaryTree.setLeft(BinaryTree(1))
binaryTree.setRight(BinaryTree(2))
binaryTree.getLeft().setLeft(BinaryTree(3))
binaryTree.getLeft().setRight(BinaryTree(4))
binaryTree.getRight().setLeft(BinaryTree(5))
binaryTree.getRight().setRight(BinaryTree(6))

实例化好的二叉树是长这个样子的：

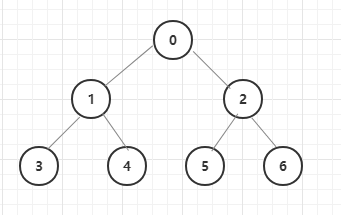
前序遍历

接下来，我们对这棵树进行前序遍历。在此之前，我们介绍一下什么是前序遍历。

前面我们介绍过了树的深度优先遍历和广度优先遍历，这里就不再赘述了。

前序遍历的顺序就是先遍历树的父节点，然后遍历树的左节点，然后遍历树的右节点，以此类推。

对于我们上面定义好的二叉树来说，它的前序遍历结果就是：0 -> 1 -> 3 -> 4 -> 2 -> 5 -> 6

对于前序、中序、后序遍历来说，采用递归的方式是非常方便的。这里我们就用递归来实现一下：

def preorderTraversal(now, result=[]):
    if now == None:
        return result
    result.append(now.data)
    preorderTraversal(now.left, result)
    preorderTraversal(now.right, result)
    return result
print(preorderTraversal(binaryTree))

执行结果：[0, 1, 3, 4, 2, 5, 6]，是不是和我们之前手动遍历的结果一样呢。

中序遍历

中序遍历的顺序是：先遍历树的左节点，再遍历树的父节点，再遍历树的右节点。

对于我们上面创建的二叉树，它的中序遍历结果就是：3 -> 1 -> 4 -> 0 -> 5 -> 2 -> 6

在前序遍历的时候是先遍历父节点，所以result.append(now.data)，就在遍历左节点和右节点的前面。

而中序遍历要先遍历左节点，所以result.append(now.data)就要在遍历左节点的后面，遍历右节点的前面。

def intermediateTraversal(now, result=[]):
    if now == None:
        return result
    intermediateTraversal(now.left, result)
    result.append(now.data)
    intermediateTraversal(now.right, result)
    return result
print(intermediateTraversal(binaryTree))

执行结果：[3, 1, 4, 0, 5, 2, 6]

后序遍历

后序遍历顺序是：先遍历树的左节点，再遍历树的右节点，再遍历树的父节点。

对于我们上面创建的二叉树，它的后序遍历结果是：3 -> 4 -> 1 -> 5 -> 6 -> 2 -> 0

相应的递归方程为：

def postorderTraversal(now, result=[]):
    if now == None:
        return
    postorderTraversal(now.left, result)
    postorderTraversal(now.right, result)
    result.append(now.data)
    return result
print(postorderTraversal(binaryTree))

执行结果：[3, 4, 1, 5, 6, 2, 0]

好，今天我们关于二叉树的三序遍历就介绍到这里了，接下来我们会接着介绍更多的二叉树类型以及应用，记得关注我的文章。关于三序遍历，你还有其他的实现方法吗，留言告诉我们把。