BFS和DFS

1.图的两种遍历方式

图的遍历通常有两种方式，即深度优先搜索(Depth First Search)和广度优先搜索(Breadth First Search)。前者类似于树的先序遍历，而后者类似于树的层次遍历。

2.深搜的实现

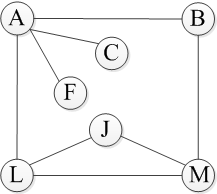
从节点A开始，找到第一个邻接点B，接着按照深搜的策略，寻找B的第一个邻接节点，结果是A，但是A已经被访问过了，所以应该选择节点M访问。同B一样，M找到邻接节点B、L和J，B被访问过，而L和J选择存储位置靠前的节点——L。接着L找到J，但是J的邻接节点全部都被访问过，因此退回节点L，同样L的所有邻接节点也全部被访问过，退回到节点M，B直到A。A访问第二个邻接点C，C没有被访问过且没有邻居节点，再退回到A，A访问F，最后一个L已被访问。

    public void DFS(int i, boolean [] visited)
    {
        if (visited[i] == false)
        {System.out.print(vertex.get(i)); visited[i] = true;}
        for (int j = 0; j < visited.length; j++)
        {
            if(adj[i][j]  == 1 && visited [j]  == false)
                DFS(j,visited);
        }
    }

    public void DFS()
    {
        boolean [] visited = new boolean [Vnum];
        for (int i = 0; i < visited.length; i++)
            visited[i] = false;

        for (int i = 0; i < visited.length; i++)
            if(!visited[i])
                DFS(i,visited);

    }

测试代码

        int number = 7;
        Graph <Character> g= new Graph<>(number);
        for (int j = 0; j < number; j++)
            g.addVertex((char)('A' + j));

        g.addEdge(1,2);
        g.addEdge(1,3);
        g.addEdge(1,4);
        g.addEdge(1,5);
        g.addEdge(2,7);
        g.addEdge(5,6);
        g.addEdge(5,7);
        g.addEdge(7,6);
        g.DFS();

深度搜索结果为ABGEFCD(其中D,E,F,G代替图中的F,L,J,M)

3.广搜的实现

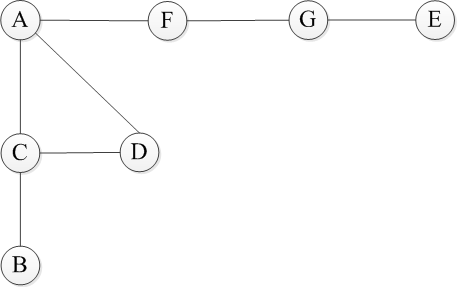
首先从A开始访问，接着按顺序访问邻接点C，D和F。然后从C开始访问邻接点B(D被访问过了)，接着是D，F的邻接点。最终顺序应该是ACDFBGE。既然是借鉴树的层次遍历，可以使用如下示意图表示广度搜索。

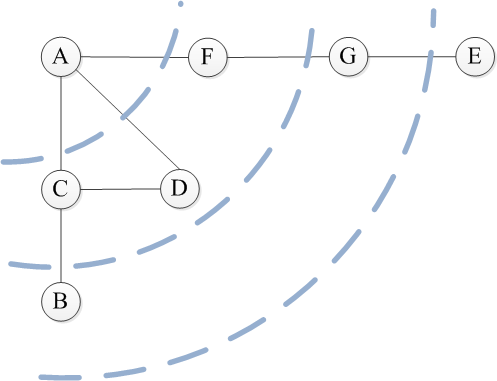
    public void BFS()
    {
        boolean [] visited = new boolean [Vnum];
        Queue q = new Queue();
        q.AddQueue(0);

        for (int i = 0; i < visited.length; i++)
            visited[i] = false;

        while  (!q.isEmpty()){

            int m = q.OutQueue();
            if (visited[m] == false) {
                visited[m] = true;
                System.out.print(vertex.get(m));
            }
            for (int j = 0; j < visited.length; j++)
            {
                if(adj[m][j]  == 1 && visited [j]  == false)
                {
                    q.AddQueue(j);
                }
            }

        }

    }

测试

        g.addEdge(2,3);
        g.addEdge(1,3);
        g.addEdge(1,4);
        g.addEdge(1,6);
        g.addEdge(3,4);
        g.addEdge(5,7);
        g.addEdge(7,6);
        g.BFS();

结果ACDFBGE

全部代码查看Graph