Codeforces Round #542 [Alex Lopashev Thanks-Round] (Div. 1) 题解

A. Toy Train

• 时间限制：2 seconds
• 内存限制：256 megabytes

题意

有编号111~n(n≤5000)n(n\le 5000)n(n≤5000)的车站顺时针呈环排列，有m(m≤20000)m(m\le 20000)m(m≤20000)个糖果需要运送到指定位置。每个糖果由(a[i],b[i])(a[i],b[i])(a[i],b[i])表示，其中a[i]≠b[i]a[i]=\not b[i]a[i]≠​b[i]，指这个糖果最初位置和需要运送到的位置。列车只能顺时针行驶，行驶到相邻站台所用时间为111。每到一个站台，最多只能取走一个糖果放在车上，这个糖果可以随便选。而卸下糖果的数量不限制。询问列车从每个位置出发把所有糖果都运送到指定位置的最短时间。

下图中蓝色的数字就表示该糖果要去的位置。

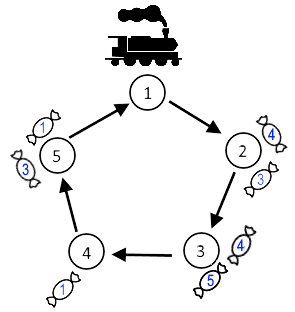
分析

假设第iii个车站有sz[i]sz[i]sz[i]个糖果，显然对于这个车站必须要至少经过sz[i]sz[i]sz[i]次。那么决定最后在哪个地方停止一定是最后一个糖果。根据贪心的策略，我们只要把最近的糖果最后取就行了。

所以我们枚举起始点iii，再枚举每一个车站jjj，如果jjj车站有糖果的话，取完车站jjj的至少需要走的时间就是dist(i,j)+(sz[j]−1)∗n+min⁡a[k]=jdist(j,b[k])dist(i,j)+(sz[j]-1)*n+\min \limits_{a[k]=j} dist(j, b[k])dist(i,j)+(sz[j]−1)∗n+a[k]=jmin​dist(j,b[k])。所有的取最大值就是答案了。

dist(i,j)dist(i,j)dist(i,j)表示从iii走到jjj的距离，具体值等于(j−i+n)%n(j-i+n)\%n(j−i+n)%n

代码如下

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 5005;
int n, m, sz[MAXN], mn[MAXN];
inline int dist(const int &A, const int &B) { return B >= A ? B-A : n+B-A; }
int main () {
   scanf("%d%d", &n, &m);
   memset(mn, 0x7f, sizeof mn);
   for(int x, y, i = 1; i <= m; ++i) {
       scanf("%d%d", &x, &y); ++sz[x];
       mn[x] = min(mn[x], dist(x, y));
   }
   for(int i = 1; i <= n; ++i) {
       int ans = 0;
       for(int j = 1; j <= n; ++j) if(sz[j])
           ans = max(ans, dist(i, j) + n*(sz[j]-1) + mn[j]);
       printf("%d ", ans);
   }
}

---

B. Wrong Answer

• 时间限制：1 seconds
• 内存限制：256 megabytes
  
  这题目好啊

题意

有这样一个问题，给出长度为nnn的整数序列aaa，求max⁡1≤l≤r≤n∑l≤i≤r(r−l+1)∗ai\large \max \limits_{1\le l\le r\le n} \sum_{l\le i\le r}(r-l+1)*a_i1≤l≤r≤nmax​∑l≤i≤r​(r−l+1)∗ai​。

其中n≤2000,∣ai∣≤106n\le2000,|a_i|\le10^6n≤2000,∣ai​∣≤106。

AliceAliceAlice同学玩够各类博弈游戏发现自己老是输给BobBobBob，决定卧薪尝胆好好刷题。她遇到了这个问题，然后写了这样一个代码：

function find_answer(n, a)
    # Assumes n is an integer between 1 and 2000, inclusive
    # Assumes a is a list containing n integers: a[0], a[1], ..., a[n-1]
    res = 0
    cur = 0
    k = -1
    for i = 0 to i = n-1
        cur = cur + a[i]
        if cur < 0
            cur = 0
            k = i
        res = max(res, (i-k)*cur)
    return res

显然这个代码是Wrong Answer\color{red}{Wrong\ Answer}Wrong Answer的。举个例子，假设n=4n=4n=4 且 a=[6,−8,7,−42]a=[6,−8,7,−42]a=[6,−8,7,−42]。那么find_answer(n,a)find\_answer(n, a)find_answer(n,a) 得到的答案是 777， 然正确答案是3⋅(6−8+7)=153⋅(6−8+7)=153⋅(6−8+7)=15。

给出k(1≤k≤109)k(1\le k\le 10^9)k(1≤k≤109)，你要构造一组数据，使得AliceAliceAlice的答案和正确答案相差恰好为kkk。你构造的序列必须也满足上面所说的n≤2000,∣ai∣≤106n\le2000,|a_i|\le10^6n≤2000,∣ai​∣≤106。如果不存在请输出−1-1−1。

分析

可以看出AliceAliceAlice的程序只统计了非负数的区间。那么我们只需要搞一个−1-1−1在最前面，然后让后面序列的和SumSumSum尽量的大。这是AliceAliceAlice的答案一定是的和SumSumSum乘以后面的长度LLL，但是多取这个−1-1−1会让答案变成(Sum−1)∗(L+1)=Sum∗L+Sum−L−1(Sum-1)*(L+1)=Sum*L+Sum-L-1(Sum−1)∗(L+1)=Sum∗L+Sum−L−1。我们只要保证Sum−L−1=kSum-L-1=kSum−L−1=k就行了,即Sum=L+1+kSum=L+1+kSum=L+1+k。

那么我们构造出来的序列除去前面的-1就是长度为LLL，和为L+1+kL+1+kL+1+k的序列。因为我们实际上是可以补0的，那么要让后面的LLL个数和为L+1+kL+1+kL+1+k。只要前面尽量放10610^6106，就行了。不过由于这个10610^6106的限制，要求L+1+kL≤106\large \frac{L+1+k}L\le 10^6LL+1+k​≤106，因为k≤109k\le10^9k≤109，L≤2000L\le 2000L≤2000，所以LLL随便取个120012001200就行了。

代码如下

#include <bits/stdc++.h>
using namespace std;
int main () {
    int k;
    scanf("%d", &k);
    //sum*1200 = (sum-1)*1201 - k
    //sum = k + 1201
    int sum = k + 1201;
    printf("1201\n-1");
    for(int i = 1; i <= 1200; ++i) {
        int ans = min(1000000, sum);
        sum -= ans;
        printf(" %d", ans);
    }
}

---

C. Morse Code

• 时间限制：2 seconds
• 内存限制：256 megabytes

题意

把二十六个字母的摩尔斯电码用二进制表示就是一些010101串。摩尔斯电码长度从111~444不等，但是这样算出来是21+22+23+24=30=26+42^1+2^2+2^3+2^4=30=26+421+22+23+24=30=26+4，那么就有444个串没有所代表的字母。它们分别是"001100110011"，"010101010101"，"111011101110"，和"111111111111"。

最初你有一个空串，有n(n≤3000)n(n\le 3000)n(n≤3000)次添加，每次添加1/01/01/0，每添加一次都要输出当前得到的串的所有子串能够翻译出的不同的字母串的数量，答案膜109+710^9+7109+7输出。比如"111"能够翻译出的就是这些：

“T” (translates into “1”)

“M” (translates into “11”)

“O” (translates into “111”)

“TT” (translates into “11”)

“TM” (translates into “111”)

“MT” (translates into “111”)

“TTT” (translates into “111”)

分析

假设你有一个固定的串，求它能够翻译出的不同字母串的dp还是很好想的。时间复杂度是O(len∗4)O(len*4)O(len∗4)。那么一个暴力的想法就是枚举每个不同子串做dp，这样dp的总时间复杂度是O(n3)O(n^3)O(n3)。

然而我们发现当左端点lll固定的时候，右端点rrr递增时其实可以一起dp的。那么对于左端点固定的子串，dp就是O(n)O(n)O(n)的。

然而这个是每一次在最后添加一个字符。不能固定左端点。

怎么办呢？

那就固定右端点倒着dp呗。

然后我判重用hash+maphash+maphash+map，多了一个logloglog再加上dp有个444的常数就TLETLETLE了。

怎么办呢，这时候又用到上面那个共用的思想(…)，我们用trie树来判010101串的重，如果到最后一个字符的个节点已经有值了那么已经算过，就不加到答案里面；否则就统计答案。右端点固定的话左端点递减的串在trie树上是一条路径，这样的话插入这些右端点固定的子串时间复杂度就是O(n)O(n)O(n)的了。

右端点有nnn个，那么总时间复杂度就是O(n2)O(n^2)O(n2)的了。

代码如下

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 3010;
const int mod = 1e9 + 7;
int n, x[MAXN], dp[MAXN], ans, trie[MAXN*MAXN][2];
inline bool chk(int i) {
    if(!x[i-3] && !x[i-2] && x[i-1] && x[i]) return 0;
    if(!x[i-3] && x[i-2] && !x[i-1] && x[i]) return 0;
    if(x[i-3] && x[i-2] && x[i-1] && !x[i]) return 0;
    if(x[i-3] && x[i-2] && x[i-1] && x[i]) return 0;
    return 1;
}
inline void add(int &x, int y) { x += y; if(x >= mod) x -= mod; }
int main () {
    scanf("%d", &n);
    for(int i = 1; i <= n; ++i)
        scanf("%d", &x[i]);
    int rt = 1, cnt = 1;
    for(int i = 1; i <= n; ++i) {
        dp[i+1] = 1;
        int r = rt;
        for(int j = i; j; --j) {
        	dp[j] = 0;
            add(dp[j], dp[j+1]);
            add(dp[j], dp[j+2]);
            add(dp[j], dp[j+3]);
            if(chk(j+3)) add(dp[j], dp[j+4]);
            if(!trie[r][x[j]]) trie[r][x[j]] = ++cnt, add(ans, dp[j]);
            r = trie[r][x[j]];
        }
        printf("%d\n", ans);
    }
}

---

D. Isolation

• 时间限制：3 seconds
• 内存限制：256 megabytes

题意

给出长度为n(1≤n≤105)n(1\le n\le 10^5)n(1≤n≤105)的数组a(ai≤n)a(a_i\le n)a(ai​≤n)。给出1≤k≤n1\le k\le n1≤k≤n。求把这个序列分成若干块的方案，使得对于每个区间，只出现一次的数字不超过kkk个。

分析

首先暴力O(n2)O(n^2)O(n2)dp很好想的，转移方程式为：

dp[i]+=dp[j−1] 且(i,j)dp[i]+=dp[j-1]\ 且(i,j)dp[i]+=dp[j−1] 且(i,j)中只出现一次的数不超过kkk个

我们看看怎么记录只出现一次的数的个数，就是从后往前扫，遇到数的第一次+1，第二次-1，然后做一个后缀和就行了。那么对于后缀和≤k\le k≤k的位置jjj，j−1j-1j−1就能够当作决策点。为了方便我们把dp[]dp[]dp[]的下标同时加一就行了。

这样的话每往后移动就修改两个区间(画画就知道了)，区间修改可以用线段树，但是穿插着查询的话无法处理，于是分块做。每个块存一下后缀和为每个值的dpdpdp值的和，也要存一下后缀和≤k\le k≤k的dpdpdp值的和，也就是这个块内的答案。也要维护懒标记。

时间复杂度O(nn)O(n\sqrt n)O(nn​)

代码如下

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int mod = 998244353;
const int MAXN = 100005;
const int Blocks = 405;
int n, qk, a[MAXN], pre[MAXN], lst[MAXN], dp[MAXN], f[MAXN];
int sum[Blocks][MAXN], ans[Blocks], lz[Blocks], l[Blocks], r[Blocks], bl[MAXN];
inline void add(int &x, int y) { x += y; x = x >= mod ? x - mod : x; }
inline void sub(int &x, int y) { x -= y; x = x < 0 ? x + mod : x; }
inline void Rebuild(int x) {
    for(int k = l[x]; k <= r[x]; ++k) sum[x][f[k]] = 0, f[k] += lz[x];
    lz[x] = ans[x] = 0;
    for(int k = l[x]; k <= r[x]; ++k) {
        add(sum[x][f[k]], dp[k]);
        if(f[k] <= qk) add(ans[x], dp[k]);
    }
}
inline void Update(int k, int val) {
    int x = bl[k];
    sub(sum[x][f[k]], dp[k]);
    if(f[k] <= qk) sub(ans[x], dp[k]);
    f[k] += val;
    add(sum[x][f[k]], dp[k]);
    if(f[k] <= qk) add(ans[x], dp[k]);
}
inline void Modify(int x, int y, int val) {
    int L = bl[x], R = bl[y];
    if(L == R) {
        Rebuild(L);
        for(int k = x; k <= y; ++k)
            Update(k, val);
    }
    else {
        Rebuild(L);
        for(int k = x; k <= r[L]; ++k) Update(k, val);
        Rebuild(R);
        for(int k = l[R]; k <= y; ++k) Update(k, val);
        for(int i = L+1; i < R; ++i)
            if(val == 1) {
                int tmp = qk - (lz[i]++);
                sub(ans[i], sum[i][tmp]);
            }
            else {
                int tmp = qk - (--lz[i]);
                add(ans[i], sum[i][tmp]);
            }
    }
}
inline int Query(int x) {
    int re = 0;
    Rebuild(bl[x]);
    for(int k = l[bl[x]]; k <= x; ++k)
        if(f[k] <= qk) add(re, dp[k]);
    for(int i = 1; i < bl[x]; ++i) add(re, ans[i]);
    return re;
}
int main() {
	scanf("%d%d", &n, &qk);
	for(int i = 1; i <= n; ++i) {
        scanf("%d", &a[i]);
        pre[i] = lst[a[i]];
        lst[a[i]] = i;
	}
	dp[1] = 1;
	int m = sqrt(n);
	for(int i = 1; i <= n; ++i) {
        bl[i] = (i-1)/m + 1;
        r[bl[i]] = i;
        if(!l[bl[i]])
            l[bl[i]] = i;
	}
	for(int i = 1; i <= n; ++i) {
        Modify(pre[i]+1, i, 1);
        if(pre[i])
            Modify(pre[pre[i]]+1, pre[i], -1);
        dp[i+1] = Query(i);
	}
	printf("%d\n", dp[n+1]);
}

写加法减法的时候用问号语句600ms，用if语句1400ms。。

---

E. Legendary Tree

• 时间限制：3 seconds
• 内存限制：256 megabytes

This is an interactive problem.\it{This\ is\ an\ interactive\ problem.}This is an interactive problem.

题意

给出树的节点数n(≤500)n(\le 500)n(≤500)，你的任务是确定树的结构。

你可以询问111111111111111次，每次查询&lt;{S},{T},v&gt;&lt;\{S\},\{T\},v&gt;<{S},{T},v>，格式如下

line 1:∣S∣line\ 1:|S|line 1:∣S∣

line 4:S1,S2,S3...S∣S∣line\ 4:S_1,S_2,S_3...S_{|S|}line 4:S1​,S2​,S3​...S∣S∣​

line 3:∣T∣line\ 3:|T|line 3:∣T∣

line 4:T1,T2,T3...T∣T∣line\ 4:T_1,T_2,T_3...T_{|T|}line 4:T1​,T2​,T3​...T∣T∣​

line 5:vline\ 5:vline 5:v

表示询问从∣S∣|S|∣S∣集的某个点经过vvv走到∣T∣|T|∣T∣集的某个点的简单路径条数。其中S⋂T=∅S\bigcap T=\varnothingS⋂T=∅

分析

先把1设为根

那么我们只要查询nnn次 &lt;{1},{2...n},i&gt;&lt;\{1\},\{2...n\},i&gt;<{1},{2...n},i> 就能得到iii的子树大小sz[i]sz[i]sz[i]。

我们的目标是找到所有个节点的父亲

显然父亲的szszsz比儿子大

我们把2~n的节点按szszsz排序

用一个vector存储到目前还没有找到父亲的点，这些点实际上可以看做叶节点，因为那些找到了父亲的点已经被我们从vector内删去。

按szszsz从小到大考虑，当前考虑到第iii个点，如果它有儿子，那么一定存在于vector中。如果iii是jjj的父亲，那么一定存在从1−&gt;i−&gt;j1-&gt;i-&gt;j1−>i−>j的路径，反之一定不存在(不可能有隔代的路径，因为我们是按szszsz从小到大考虑，隔代的情况不会出现 因为中间那一代szszsz小会被先考虑)。所以我们可以用一次查询&lt;{1},{S},i&gt;&lt;\{1\},\{S\},i&gt;<{1},{S},i>来判断叶节点集SSS内是否有iii的儿子。那么我们二分找到最左边的一个儿子，将它删去，并把它的父亲设为iii。这样一直做下去，就行了。一个点只会被删一次，查询log nlog\ nlog n次。

总查询次数是O(n+n logn)O(n+n\ logn)O(n+n logn)

时间复杂度是O(n2logn)O(n^2logn)O(n2logn)

#include<bits/stdc++.h>
using namespace std;
vector<int>S, T, vec;
#define pb push_back
const int MAXN = 505;
int n, sz[MAXN], c[MAXN], fa[MAXN];
inline int query(int x) {
    printf("%d\n", S.size());
    for(auto v:S) printf("%d ", v);
    printf("\n%d\n", T.size());
    for(auto v:T) printf("%d ", v);
    printf("\n%d\n", x);
    fflush(stdout);
    int re; scanf("%d", &re);
	return re;
}
inline bool chk(int x, int pos) {
	T.clear();
	for(int i = 0; i <= pos; ++i)
		T.pb(vec[i]);
	return query(x);
}
inline void getchild(int x) {
	while(!vec.empty()) {
		int l = 0, r = vec.size()-1, pos = -1;
		while(l <= r) {
			int mid = (l + r) >> 1;
			if(chk(x, mid)) pos = mid, r = mid-1;
			else l = mid+1;
		}
		if(~pos) {
			fa[vec[pos]] = x;
			swap(vec[pos], vec.back());
			vec.pop_back();
		}
		else return;
	}
}
inline bool cmp(int A, int B) { return sz[A] < sz[B]; }
int main() {
	scanf("%d", &n);
	S.pb(1);
	for(int i = 2; i <= n; ++i) T.pb(i), c[i-1] = i;
	for(int i = 2; i <= n; ++i) sz[i] = query(i);
	sort(c + 1, c + n, cmp);
	for(int i = 1; i < n; ++i) {
		int x = c[i];
		getchild(x);
		vec.pb(x);
	}
	puts("ANSWER");
	for(int i = 2; i <= n; ++i)
		printf("%d %d\n", fa[i]?fa[i]:1, i);
}//最后自动fflush

这道题200组数据又是交互题很慢直接评测了5min。。。