NLP传统基础（2）---LDA主题模型---学习文档主题的概率分布（文本分类/聚类）

一、简介

https://cloud.tencent.com/developer/article/1058777

1、LDA是一种主题模型

作用：可以将每篇文档的主题以概率分布的形式给出【给定一篇文档，推测其主题分布】。我们的目标是找到每一篇文档的主题分布和每一个主题中词的分布。

　　从而通过分析一些文档抽取出它们的主题（分布）出来后，便可以根据主题（分布）进行主题聚类或文本分类。

2、同时，它是一种典型的词袋模型

即一篇文档是由一组词构成，词与词之间没有先后顺序的关系。

此外，一篇文档可以包含多个主题，文档中每一个词都由其中的一个主题生成。

3、理解LDA，可以分为下述5个步骤：

1. 一个函数：gamma函数
2. 四个分布：二项分布、多项分布、beta分布、Dirichlet分布
3. 一个概念和一个理念：共轭先验和贝叶斯框架
4. 两个模型：pLSA、LDA（在本文第4 部分阐述）
5. 一个采样：Gibbs采样

二、LDA模型

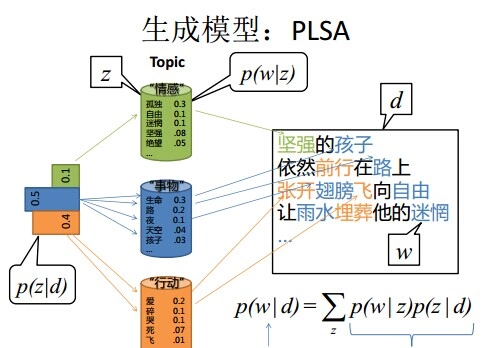
比如假设事先给定了这几个主题：Arts、Budgets、Children、Education，然后通过学习的方式，获取每个主题Topic对应的词语。如下图所示：

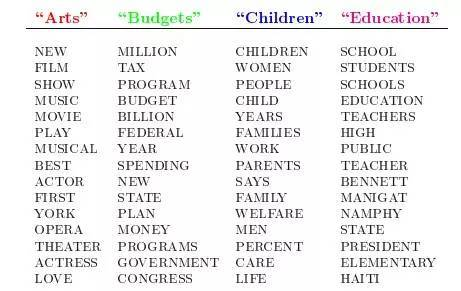
然后以一定的概率选取上述某个主题，再以一定的概率选取那个主题下的某个单词，不断的重复这两步，最终生成如下图所示的一篇文章（其中不同颜色的词语分别对应上图中不同主题下的词）：

而当我们看到一篇文章后，往往喜欢推测这篇文章是如何生成的，我们可能会认为作者先确定这篇文章的几个主题，然后围绕这几个主题遣词造句，表达成文。LDA就是要干这事：根据给定的一篇文档，推测其主题分布。

LDA的图模型：

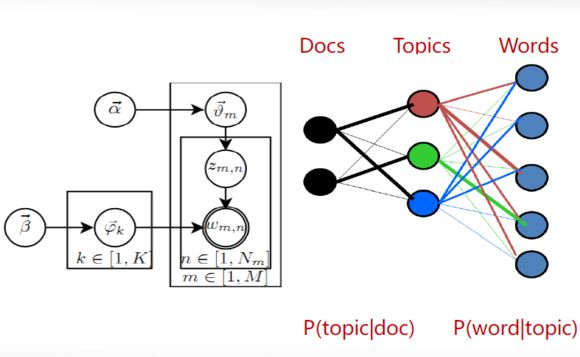
共有M篇文档，每个文档有Nm个单词，一共涉及到K个主题；

每篇文档都有各自的主题，主题分布是多项式分布，该多项式分布的参数服从Dirichlet分布，该Dirichlet分布的参数为α；

每个主题都有各自的词分布，词分布为为多项式分布，该多项式分布的参数服从Dirichlet分布，该Dirichlet分布的参数为β；

对于某篇文档d中的第n个词，首先从该文档的主题分布中采用一个主题，然后再这个主题对应的词分布中采用一个词，不断重复该操作，直到m篇文档全部完成上述过程。

LDA用生成式模型的角度来看待文档和主题。

　　假设每篇文档包含了多个主题，

　　用θ_d表示文档t每个话题所占比例，

　　θ_d，k表示文档t中包含主题d所占用的比例，继而通过如下过程生成文档d。

　　（1）根据参数为α的狄利克雷分布，随机采样一个话题分布θ_d；

　　（2）按照如下步骤生成文中的N个词：

　　　　　　根据θ_d进行话指派，得到文档d中词n的话题

　　　　　　根据指派话题所对应的词频β_k进行采样随机生成词

三、两个模型：PLSA、LDA

我们来看一个例子，如图所示：

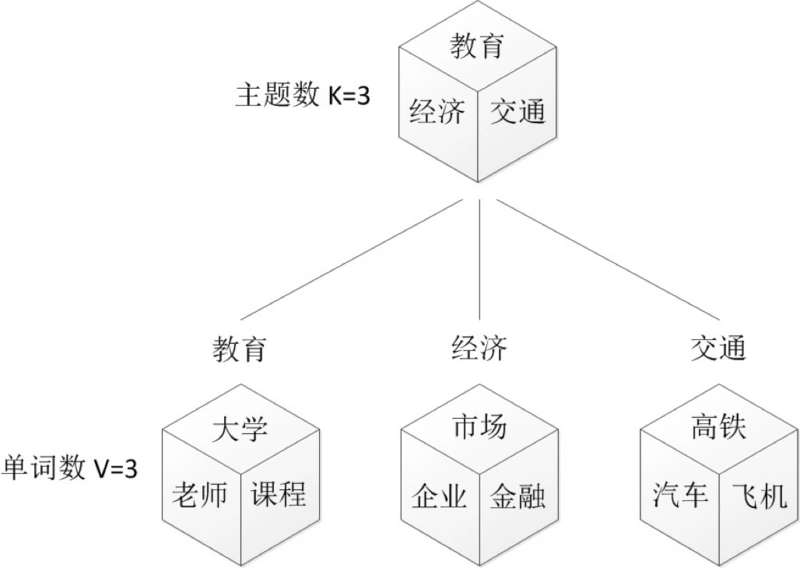
上图中有三个主题，在PLSA中，我们会以固定的概率来抽取一个主题词，比如0.5的概率抽取教育这个主题词，然后根据抽取出来的主题词，找其对应的词分布，再根据词分布，抽取一个词汇。由此，可以看出PLSA中，主题分布和词分布都是唯一确定的。但是，在LDA中，主题分布和词分布是不确定的，LDA的作者们采用的是贝叶斯派的思想，认为它们应该服从一个分布，主题分布和词分布都是多项式分布，因为多项式分布和狄利克雷分布是共轭结构，在LDA中主题分布和词分布使用了Dirichlet分布作为它们的共轭先验分布。所以，也就有了一句广为流传的话 -- LDA 就是 PLSA 的贝叶斯化版本。下面两张图片很好的体现了两者的区别：

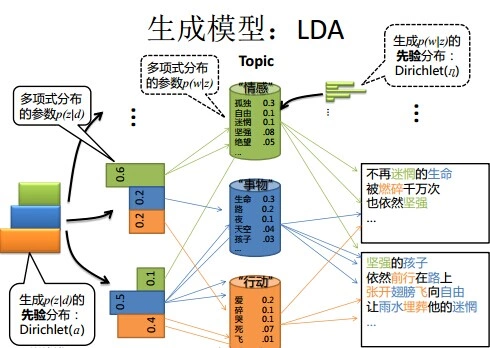
四、模型生成过程：

https://www.cnblogs.com/pinard/p/6831308.html

https://blog.csdn.net/liuy9803/article/details/81091022
LDA从生成式模型的角度看待文档和主题，认为语料库中所有文档是隐含主题的随机混合，每个主题是由所有单词分布体现的。文档m的生成过程为：

（1）根据参数为α的Dirichlet分布选择一个主题分布，\theta _{m}\sim Dir(\alpha )；

（2）根据参数为η的Dirichlet分布选择一个单词分布，\beta _{k}\sim Dir(\eta )；

（3）按照下列步骤生成文档m中的N_{m}个单词：

a、根据\theta _{m} 指派主题，得到文档m中单词n的主题 z_{mn}\sim Multinomial(\theta _{m})；

b、根据指派的主题z_{mn} 所对应的单词分布\beta _{k} 生成单词 w_{mn}\sim Multinomial(\beta _{z_{mn}})。