维特比算法及python实现

先放一张找到的算法流程图：

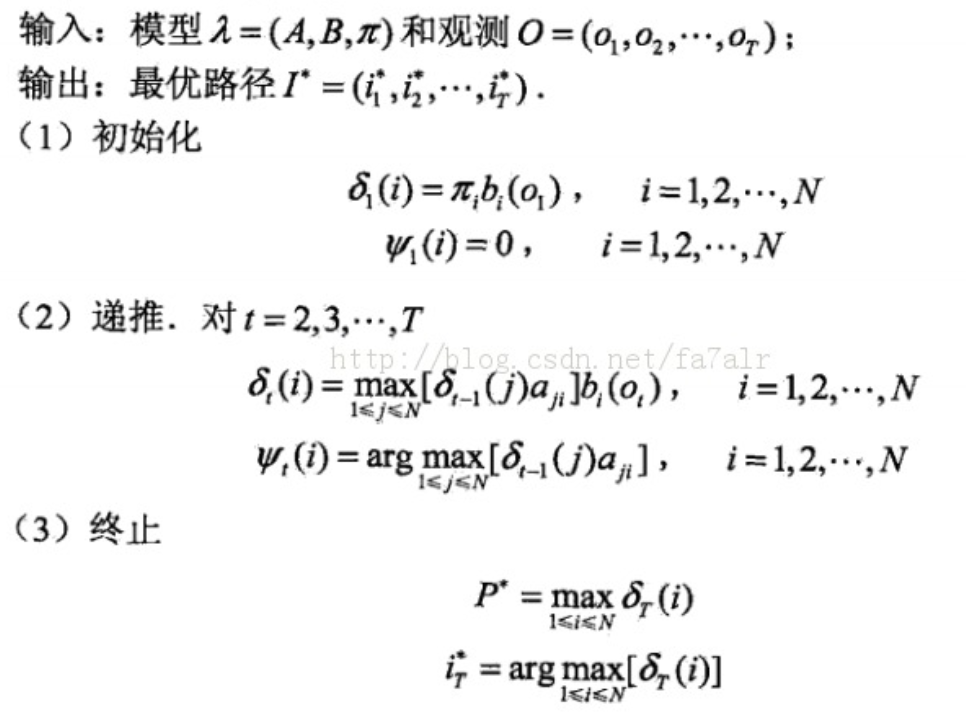
上图解释：

A：状态转移概率矩阵，Aij表示状态i到状态j转换的概率，即P(state=j | state=i)。下面代码中以P表示。

B：观测矩阵，Bij表示给定状态i，观测结果为j的概率。即P(observation=j | state=i)

π：初始时状态概率分布，表示各状态出现的概率。代码中以pi表示。

O：输入的观测序列。

：表示经过节点（时刻t，状态state=i）的局部最优路径到此节点时对应的概率，即给定X=(x1,...xt,...xn)子序列(x1,x2,...xt)时，对应的最佳状态序列（末状态state=i）的概率值。

下面代码中以delta表示

：跟上面相关。表示上面最优路径经过的节点的上一个状态id。下面代码中以w表示。

1式理解：右边为状态state=i出现的概率乘以（状态i下观测到O[t=1]的概率）

2式理解：当前节点概率值，为（上一时刻各节点概率值乘以状态转换概率）的最大值，再乘以状态state=i时观测到O[t]的概率。这就是动态规划的思想了。

以上，熟悉隐马尔可夫模型的话，理解应该没问题了。

-------------------------------------------------------------------------

下面进入代码部分：

import  numpy as np
def my_viterbi(O,P,B,pi):
    '''
    O：观测序列
    P：状态转移矩阵，Pij表示状态i到j转换的条件概率
    B：观测矩阵，Bij表示状态i下观测到Oj的条件概率
    pi：初始的状态概率分布

    return:各个时刻选择的状态id
    '''

    set_O=list(set(O))
#     观测结果有多少种类
    class_observe=len(set_O)
#     将观测序列one-hot化，不然会超过索引
    for i in range(len(O)):
        O[i]=set_O.index(O[i])
#     进行若干检查
    assert class_observe==B.shape[1],'观测序列与观测矩阵的观测结果维度不一致！'
    assert P.shape[0]==B.shape[0],'转移矩阵与观测矩阵的状态维度不一致！'
    assert P.shape[0]==len(pi),'转移矩阵与状态分布的状态维度不一致！'
    sequence_len=len(O)# 观测序列长度，即有多少个时刻t
    states_per_time=P.shape[0]# 每个时刻有多少个状态，这里假设相同。实际可以不同，不同的话，应该要给出每个时刻对应的状态集合。这里默认所有状态
#     记录（局部）最优路径中节点（t时刻状态s）的概率值，当记录完毕后，逆序寻找最优节点即可
    delta=np.zeros((sequence_len,states_per_time))
#     记录经过t时刻状态s的局部最优路径的前一个状态id
    w=np.zeros((sequence_len,states_per_time))
#     初始化
    for s in range(states_per_time):
        delta[0,s]=pi[s]*B[s,O[0]]# 即状态概率分布乘以观测矩阵对应元素，得到0时刻各状态对应概率值
    for t in range(1,sequence_len):
        for s in range(states_per_time):
            delta[t,s]=np.max([delta[t-1,s_]*P[s_,s] for s_ in range(states_per_time)])*B[s,O[t]]
            w[t,s]=np.argmax([delta[t-1,s_]*P[s_,s] for s_ in range(states_per_time)])
    max_sequence_prob=np.max(delta[-1,:])
    res=np.zeros(sequence_len).astype(np.int32)
    res[-1]=np.argmax(delta[-1,:])
    for t in range(sequence_len-2,-1,-1):
        res[t]=w[t+1,res[t+1]]
    return res,max_sequence_prob

# 状态转移矩阵
P=np.array([[0.5,0.2,0.3],[0.3,0.5,0.2],[0.2,0.3,0.5]])
# 状态生成观测矩阵
B=np.array([[0.5,0.5],[0.4,0.6],[0.7,0.3]])
# 观测序列，假设有2种观察结果，比如扔硬币，从0开始
O=np.array([2,3,3])
# 初始时各个状态出现的概率
pi=np.array([0.2,0.4,0.4])
res,prob=my_viterbi(O, P, B, pi)
print(res)

输出：

array([2,1,1])

总结

涉及到的知识点为隐马尔可夫模型和动态规划。比较简单。