Python之网络模型与图形绘制工具networkx

笔记

# https://www.jianshu.com/p/e543dc63454f
import networkx as nx
import matplotlib.pyplot as plt

 ############################################################################# (创建)初始化图模型
"""
nx.Graph() 简单无向图
g = nx.DiGraph() 简单有向图
g = nx.Grap(),DiGraph() 有自环
nx.MultiGraph(), nx.MultiDiGraph() 有重边
"""
g = nx.Graph()
g.clear()  # 将图上元素清空

 ############################################################################## 添加节点
"""
+ 节点可以是任意数据类型
+ 添加一个节点 g.add_node(ele)
    g.add_node(1)
    g.add_node("a")
    g.add_node("spam")
+ 添加一组节点：提前构建好了一个节点列表，将其一次性加进来，这跟后边加边的操作是具有一致性的 g.add_nodes_from(eles)
    g.add_nodes_from([2,3])
    g.add_nodes_from(a)  # 其中,a = [2,3]
+ 区别：
    g.add_node("spam") # 添加了一个名为spam的节点
    g.add_nodes_from("spam") # 添加了4个节点，名为s,p,a,m
    g.nodes() # 可将以上5个节点打印出来看看
+ 其它： 加一组从0开始的连续数字的节点
    H = nx.path_graph(10)
    g.add_nodes_from(H) # 将0~9加入了节点 # #但请勿使用g.add_node(H)
"""
# g.add_node("spam") # 添加了一个名为spam的节点
# g.add_nodes_from(["a","b","c","d","e","f"]) # 添加了4个节点，名为s,p,a,m

H = nx.path_graph(4)
g.add_nodes_from(H) # 将0~9加入了节点 # #但请勿使用g.add_node(H)
 ############################################################################## 移除节点
"""
+ 与添加节点同理
"""
# g.remove_node(node_name)
# g.remove_nodes_from(nodes_list)

 ############################################################################## 添加边
"""
+ 边是由对应节点的名字的元组组成，加一条边
+ 加入一条边 g.add_edge(eleA,eleB)
    g.add_edge(1,2);
    e = (2,3);
    g.add_edge(*e) #直接g.add_edge(e)数据类型不对，*是将元组中的元素取出
+ 加入一组边 g.add_edges_from([(eleA,eleB),...,(eleC,eleD)])
    g.add_edges_from([(1,2),(1,3)])
    g.add_edges_from([("a","spam") , ("a",2)])
+ 加入一组系列连续的边 nx.path_graph(n)
    n = 10
    H = nx.path_graph(n)
    g.add_edges_from(H.edges()) #添加了0~1,1~2 ... n-2~n-1这样的n-1条连续的边
+ 补充
    G.add_weight_edges_from(list)
    G.add_weight_edge(1,2,3.0) # 第三个是权值
    G.add_edges_from(list) # 添加列表中的边
"""
# g.add_edge(1,2);
# e = (2,3);
# g.add_edge(*e) #直接g.add_edge(e)数据类型不对，*是将元组中的元素取出
 ##############################################################################  删除边
"""
g.remove_edge(edge)
g.remove_edges_from(edges_list)
"""

 ##############################################################################  查看图上节点和边的信息
""" g = nx.Graph(day="Monday")
g.graph # {'day': 'Monday'} # 查看图模型
g.graph['day'] = 'Tuesday' # g.graph # {'day': 'Tuesday'} # 修改图模型
g.number_of_nodes() # 查看点的数量
g.number_of_edges() # 查看边的数量
g.nodes() # 返回所有点的信息(list)
g.edges() # 返回所有边的信息(list中每个元素是一个tuple)
g.neighbors(1) # 所有与1这个点相连的点的信息以列表的形式返回

+ 节点属性设置
    g.add_node('benz', money=10000, fuel="1.5L")
    print g.node['benz'] # {'fuel': '1.5L', 'money': 10000}
    print g.node['benz']['money'] # 10000
    print g.nodes(data=True) # data默认false就是不输出属性信息，修改为true，会将节点名字和属性信息一起输出
    g[1]  #查看所有与1相连的边的属性，格式输出：{0: {}, 2: {}} 表示1和0相连的边没有设置任何属性（也就是{}没有信息），同理1和2相连的边也没有任何属性
+ Directed graphs
    + DG = nx.DiGraph()
    + DG.add_weighted_edges_from([(1,2,0.5), (3,1,0.75), (1,4,0.3)]) # 添加带权值的边
    + DG.out_degree(1) # 打印结果：2 表示：找到1的出度
    + DG.out_degree(1, weight='weight') # 打印结果：0.8 表示：从1出去的边的权值和，这里权值是以weight属性值作为标准，如果你有一个money属性，那么也可以修改为weight='money'，那么结果就是对money求和了
    + DG.successors(1) # [2,4] 表示1的后继节点有2和4
    + DG.predecessors(1) # [3] 表示只有一个节点3有指向1的连边
+ MG=nx.MultiGraph()
    MG.add_weighted_edges_from([(1,2,.5), (1,2,.75), (2,3,.5)])
    print MG.degree(weight='weight') # {1: 1.25, 2: 1.75, 3: 0.5}
    GG=nx.Graph()
    for n,nbrs in MG.adjacency_iter():
        for nbr,edict in nbrs.items():
            minvalue=min([d['weight'] for d in edict.values()])
            GG.add_edge(n,nbr, weight = minvalue)
    print nx.shortest_path(GG,1,3) # [1, 2, 3]
"""
print(g.nodes(data=True))

 ############################################################################## 绘制图像 (画布)
nx.draw(g,with_labels=True)
# nx.draw(g) # 绘制
# nx.draw(g, pos=nx.spectral_layout(g), nodecolor='y', edge_color='b');
# nx.draw_networkx(BG, pos, edges=edges, labels=labels) # BG = nx.Graph() ； edges = BG.edges()；pos = dict() ; labels = dict((n, "(" + n + "," + d['_type'] + ")") for n,d in BG.nodes(data=True))
 ############################################################################## 显示图像
"""
plt.show() # 控制台显示图像
plt.savefig("C:/Users/千千寰宇/Desktop/path.png") # 存储图像 (存储/显示)二选一
"""
plt.show()
# plt.savefig("C:/Users/千千寰宇/Desktop/path.png") # 存储图像 (存储/显示)二选一

Demo

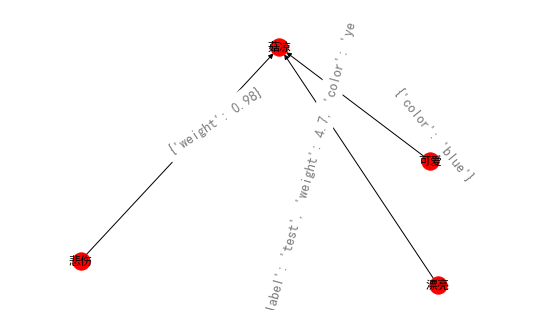
# coding = utf-8
import networkx as nx
import matplotlib.pyplot as plt

# 解决图像中的中文乱码问题
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['font.family']='sans-serif'

g = nx.DiGraph();
g.clear();

g.add_edge("可爱","菇凉",label="test",weight=4.7);
g.add_edge("漂亮","菇凉",weight=0.98);
g.add_edge("悲伤","菇凉");

g.edges["悲伤", "菇凉"]['color'] = "blue"

g["可爱"]["菇凉"]['color'] = "yellow"
print(g);
# g.add_node("可爱")
# g.add_node("漂亮");
# g.add_node("悲伤");

# g.add_node("菇凉");

print(g.nodes())
print(g.nodes().data()) # 显示边的数据
print(g.edges().data())

 # nx.draw(g,with_labels=True) # 显示节点的名称

 #  显示边的标签信息
pos=nx.spring_layout(g);
nx.draw_spring(g,with_labels=True); # 显示节点的名称
nx.draw_networkx_edge_labels(g,pos,font_size=14,alpha=0.5,rotate=True); 

plt.axis('off')
plt.show()

 # output
['可爱', '菇凉', '漂亮', '悲伤']
[('可爱', {}), ('菇凉', {}), ('漂亮', {}), ('悲伤', {})]
[('可爱', '菇凉', {'label': 'test', 'weight': 4.7, 'color': 'yellow'}), ('漂亮', '菇凉', {'weight': 0.98}), ('悲伤', '菇凉', {'color': 'blue'})]