JS写斐波那契数列的几种方法

　　斐波那契数，指的是这样一个数列：1、1、2、3、5、8、13、21、……在数学上，斐波那契数列以如下被以递归的方法定义：F0=0，F1=1，Fn=Fn-1+Fn-2（n>=2，n∈N*），用文字来说，就是斐波那契数列由 0 和 1 开始，之后的斐波那契数列系数就由之前的两数相加。　　

　　常用的计算斐波那契数列的方法分为两大类：递归和循环。

递归

方法一：普通递归

　　代码优美逻辑清晰。但是有重复计算的问题，如：当n为5的时候要计算fibonacci(4) + fibonacci(3)，当n为4的要计算fibonacci(3) + fibonacci(2) ，这时fibonacci(3)就是重复计算了。运行 fibonacci(50) 会出现浏览器假死现象，毕竟递归需要堆栈，数字过大内存不够。

function fibonacci(n) {
    if (n == 1 || n == 2) {
        return 1
    };
    return fibonacci(n - 2) + fibonacci(n - 1);
}
fibonacci(30)

方法二：改进递归-把前两位数字做成参数避免重复计算

function fibonacci(n) {
    function fib(n, v1, v2) {
        if (n == 1)
            return v1;
        if (n == 2)
            return v2;
        else
            return fib(n - 1, v2, v1 + v2)
    }
    return fib(n, 1, 1)
}
fibonacci(30)

方法三：改进递归-利用闭包特性把运算结果存储在数组里，避免重复计算

var fibonacci = function () {
    let memo = [0, 1];
    let fib = function (n) {
        if (memo[n] == undefined) {
            memo[n] = fib(n - 2) + fib(n - 1)
        }
        return memo[n]
    }
    return fib;
}()
fibonacci(30)

方法三₁：改进递归-摘出存储计算结果的功能函数

var memoizer = function (func) {
    let memo = [];
    return function (n) {
        if (memo[n] == undefined) {
            memo[n] = func(n)
        }
        return memo[n]
    }
};
var fibonacci=memoizer(function(n){
    if (n == 1 || n == 2) {
        return 1
    };
    return fibonacci(n - 2) + fibonacci(n - 1);
})
fibonacci(30)

循环

方法一：普通for循环

function fibonacci(n) {
    var n1 = 1, n2 = 1, sum;
    for (let i = 2; i < n; i++) {
        sum = n1 + n2
        n1 = n2
        n2 = sum
    }
    return sum
}
fibonacci(30)

方法二：for循环+解构赋值

var fibonacci = function (n) {
    let n1 = 1; n2 = 1;
    for (let i = 2; i < n; i++) {
        [n1, n2] = [n2, n1 + n2]
    }
    return n2
}
fibonacci(30)

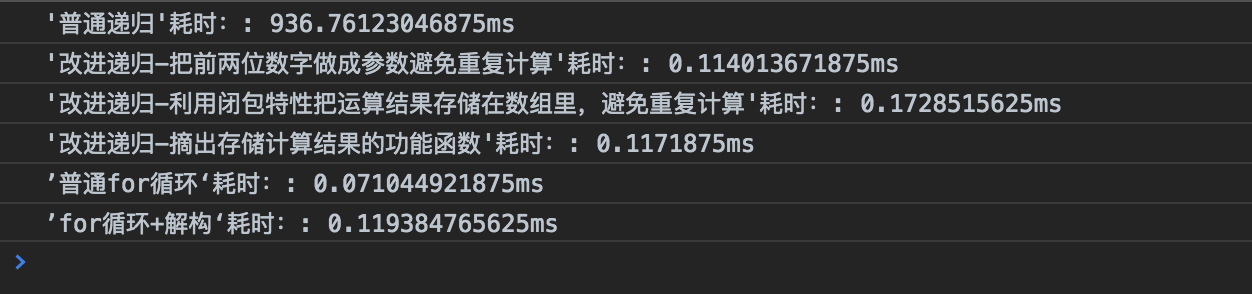
各种方法运行耗时如下图：普通递归>改进递归>for循环