POJ 1661 Help Jimmy(二维DP)

题目链接：http://poj.org/problem?id=1661

题目大意：

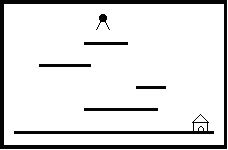
如图包括多个长度和高度各不相同的平台。地面是最低的平台，高度为零，长度无限。

Jimmy老鼠在时刻0从高于所有平台的某处（高H处）开始下落，它的下落速度始终为1米/秒。当Jimmy落到某个平台上时，游戏者选择让它向左还是向右跑，它跑动的速度也是1米/秒。当Jimmy跑到平台的边缘时，开始继续下落。Jimmy每次下落的高度不能超过MAX米，不然就会摔死，游戏也会结束。

设计一个程序，计算Jimmy到底地面时可能的最早时间。

解题思路：根据题意易得无论如何都要下落H的高度，所以可以不用计算下落高度所需时间，直接计算水平走的最短时间最后加上高度即可，按平台高度从高到低排序，建立二维数组,dp[i][0]表示第i个平台往左走到达地面的最短水平时间，dp[i][1]表示第i个平台往右走到达地面的最短水平时间，于是有状态转移方程：

dp[i][0]=min(dp[j][0]+a[i].x1-a[j].x1,dp[j][1]+a[j].x2-a[i].x1)， j是i左边下面的落点平台编号。

dp[i][1]=min(dp[j][1]+a[j].x2-a[i].x2,dp[j][0]+a[i].x2-a[j].x1)，j是i右边下面的落点平台编号。

所以直接自底向上递推，每次往左或往右找到第一个落点平台计算最少时间，最后推到i=0（起始点）就可以了。

要注意一下①初始化dp为inf，dp[0][1]和dp[0][0]也要初始化为inf。

　　　　　②找到第一个可掉落的平台计算之后，就break，不然会把下面几个平台都算进去。

　　　　　③判断当找不到落点平台时，可能有三种情况：

　　　　　　　　1）所在平台高度小于等于MAX，但下面没有平台

　　　　　　　　2）下面有平台，但两平台高度差大于MAX

　　　　　　　　3）下面没有平台，且所在平台高度大于MAX

　　　　　　特判情况1），此时dp[i][0](或dp[i][1])为0

代码：

 #include<cstdio>
 #include<algorithm>
 using namespace std;
 const int N=1e3+;
 const int inf=<<;

 struct node{
     int x1,x2,h;
 }a[N];

 int dp[N][];//从第i层0往左，1往右 

 bool cmp(node a,node b){
     return a.h>b.h;
 }

 int main(){
     int T;
     scanf("%d",&T);
     while(T--){
         int n,X,H,MAX;
         scanf("%d%d%d%d",&n,&X,&H,&MAX);
         for(int i=;i<=n;i++){
             scanf("%d%d%d",&a[i].x1,&a[i].x2,&a[i].h);
             dp[i][]=dp[i][]=inf;
         }
         sort(a+,a++n,cmp);

         //将起始点也当成一个平台
         a[].h=H;
         a[].x1=a[].x2=X;
         dp[n][]=dp[n][]=;
         dp[][]=dp[][]=inf;
         //自底向上推
         for(int i=n-;i>=;i--){
             //往左走
             for(int j=i+;j<=n;j++){
                 if(a[i].h-a[j].h<=MAX){
                     if(a[j].x1<=a[i].x1&&a[j].x2>=a[i].x1){
                         dp[i][]=min(dp[j][]+a[i].x1-a[j].x1,dp[j][]+a[j].x2-a[i].x1);
                         break;
                     }
                 }
             }
             //下面没平台且里地面高度不超过MAX
             if(a[i].h<=MAX&&dp[i][]==inf)
                 dp[i][]=;

             //往右走
             for(int j=i+;j<=n;j++) {
                 if(a[i].h-a[j].h<=MAX){
                     if(a[j].x2>=a[i].x2&&a[j].x1<=a[i].x2){
                         dp[i][]=min(dp[j][]+a[j].x2-a[i].x2,dp[j][]+a[i].x2-a[j].x1);
                         break;
                     }
                 }
             }
             if(a[i].h<=MAX&&dp[i][]==inf)
                 dp[i][]=;
         }
         printf("%d\n",min(dp[][],dp[][])+H);
     }
     return ;
 }