全连接BP神经网络

前馈神经网络

前馈神经网络(feedforward neural network)是最朴素的神经网络，通常我们所说的前馈神经网络有两种，一种叫反向传播网络(Back propagation Networks)也可简称为BP网络；一种叫做径向基函数神经网络(RBF Network)

网络结构

前馈神经网络的结构不固定，一般神经网络包括输入层、隐层和输出层，下面的图一的神经网络由两层，每层4个节点。第二个神经网络有两个隐层，第一层5个节点，第二层3个节点，最后一层输出层只有一个节点。神经网络有很多种设计模式，并在不同的模式下产生不同的效果。

　　

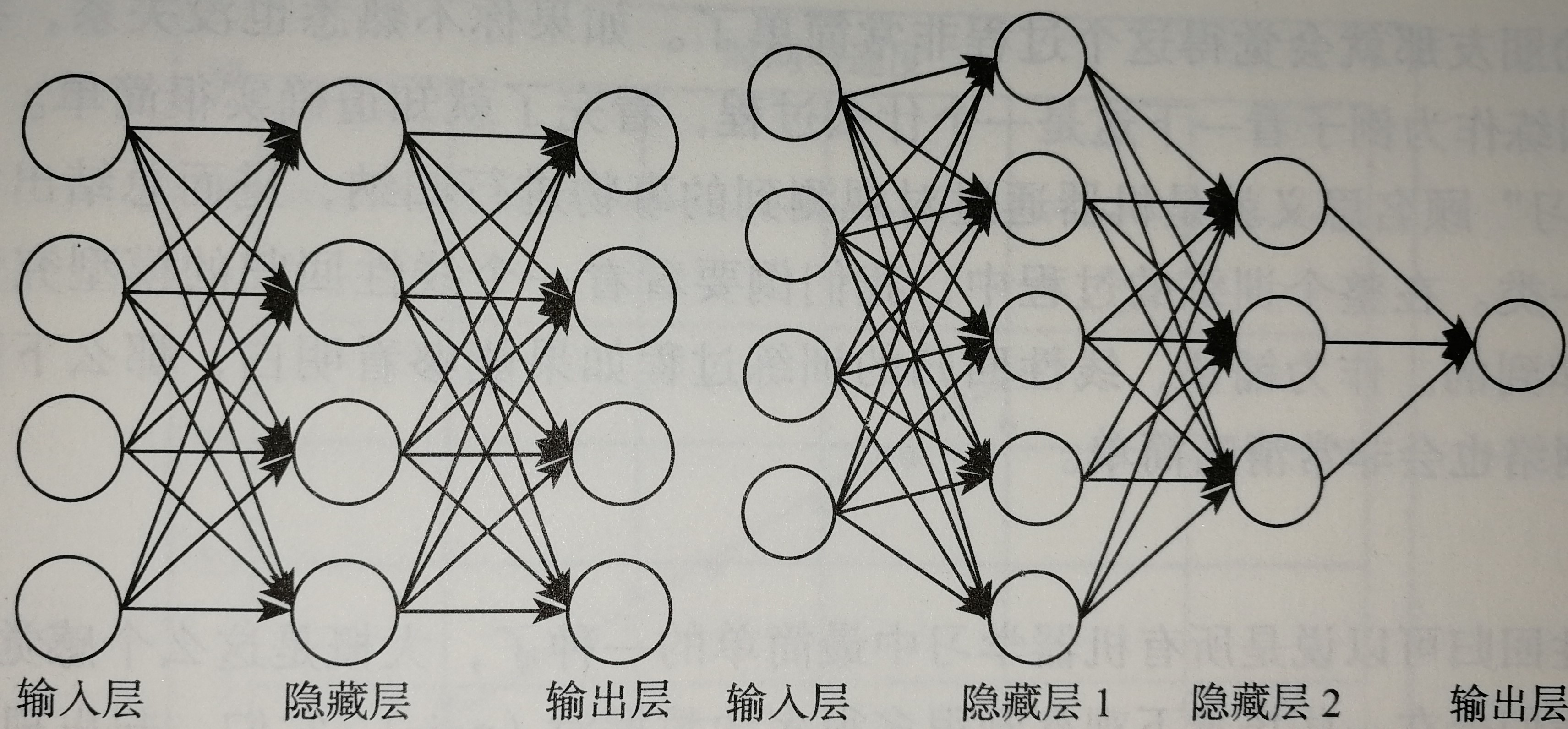
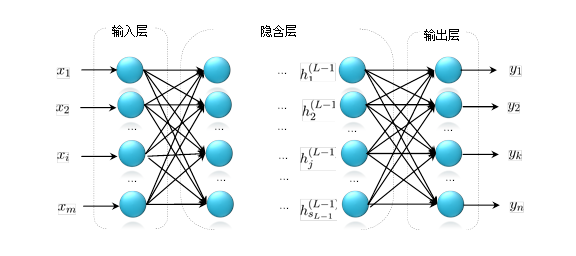
　　神经网络的复杂之处在于他的组成结构爱太复杂，神经元太多，为了方便简介，我们设计一个最简单的BP网络结构，如下图所示。

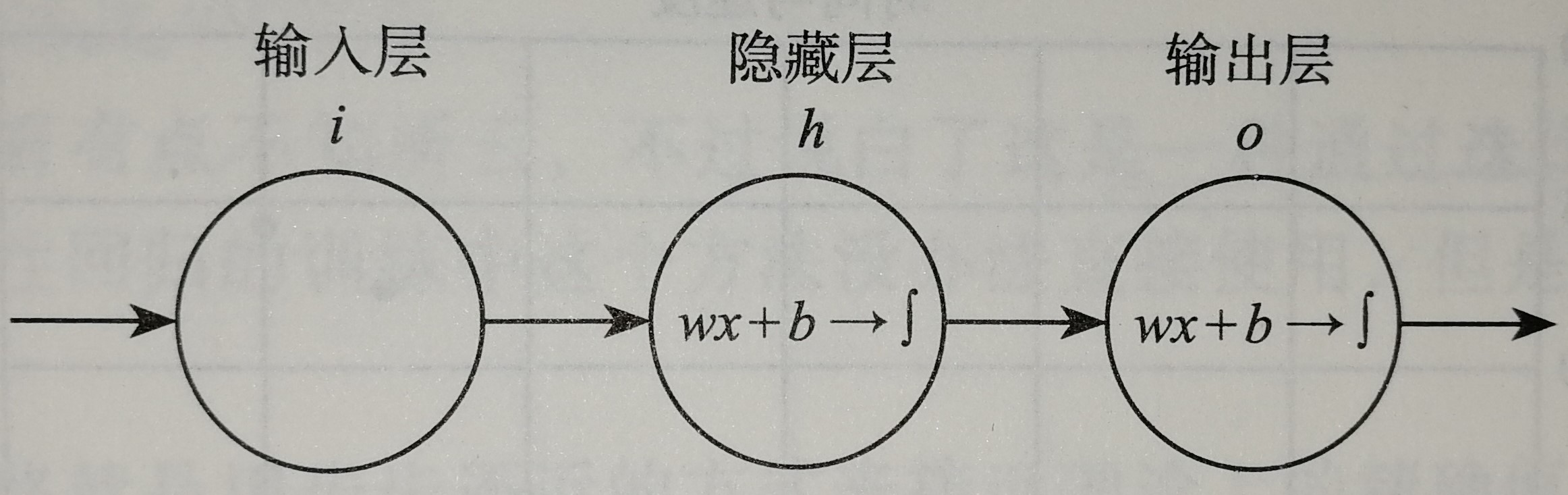
　　这是一个只有两层的神经网络，x我们也让他最简化，就一个实数，我们规定隐层h和输出层o这两层都是$z=wx+b$和$f(z)=\frac{1}{1+e^{-z}}$的组合，一旦输入样本x和标签y之后，模型就开始训练了。那么我们的问题就变成了求隐层的w、b和输出层的w、b四个参数的过程。

开始训练

　　我们想要得到$y=wx+b$中的w和b，我们有众多的样本x和标签y，在这里写作y和x的关系，假设拟合的过程中有这样的一个参数$e$代表error，表示误差的意思，$y=wx+b+e$

　　当我们有n对x和y那么就有n个$e$，我们试着把n个$e$都加起来表示一个误差总量，为了不让残差正负抵消我们取平方或者取绝对值，本文取平方。这种误差我们称为“残差”，也就是我们建模之后进行拟合出的结果和真实结果之间的差值。损失函数Loss还有一种称呼叫做“代价函数Cost”，

$$Loss=\sum_{i=1}^{n}e_i^2=\sum_{i=1}^{n}(y_i-(wx_i+b))^2$$

　　现在我们要做的就是找到一个比较好的w和b，使得整个Loss尽可能的小，越小说明我们训练出来的模型越好。

梯度下降法

　　老规矩，求最小值我们一般中梯度下降算法，通过迭代不断的优化待定系数w和b。我们的残差到底是一个怎样的函数呢，他的图形到底长什么样子呢？到底该怎么求他的最小值呢？OK,为了方便读者理解，我把Loss函数给你们画出来。

$$Loss=\sum_{i=1}^{n}(x_i^2w^2+b^2+2x_iwb-2y_ib-2x_iy_iw+y_i^2)=Aw^2+Bb^2+Cwb+Db+Dw+Eb+F$$

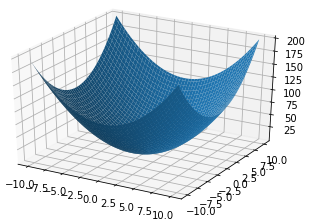
　　我们初始化一个$w_o$和$b_0$，带到Loss里面去，这个点($w_o,b_o,Loss_o$)会出现在碗壁的某个位置，而我们的目标位置是碗底，那就慢慢的一点一点的往底部挪吧。

$$x_{n+1}=x_n-\eta \frac{df(x)}{dx}$$

　　$\eta$是学习率，也就是每次挪动的步长，$\eta$大每次迭代的脚步就大，$\eta$小每次迭代的脚步就小，我们只有取到合适的$\eta$才能尽可能的接近最小值而不会因为步子太大越过了最小值。到后面每次移动的水平距离实在逐步减小的，原因就是因为整个函数圆乎乎的底部斜率在降低，吃个栗子：

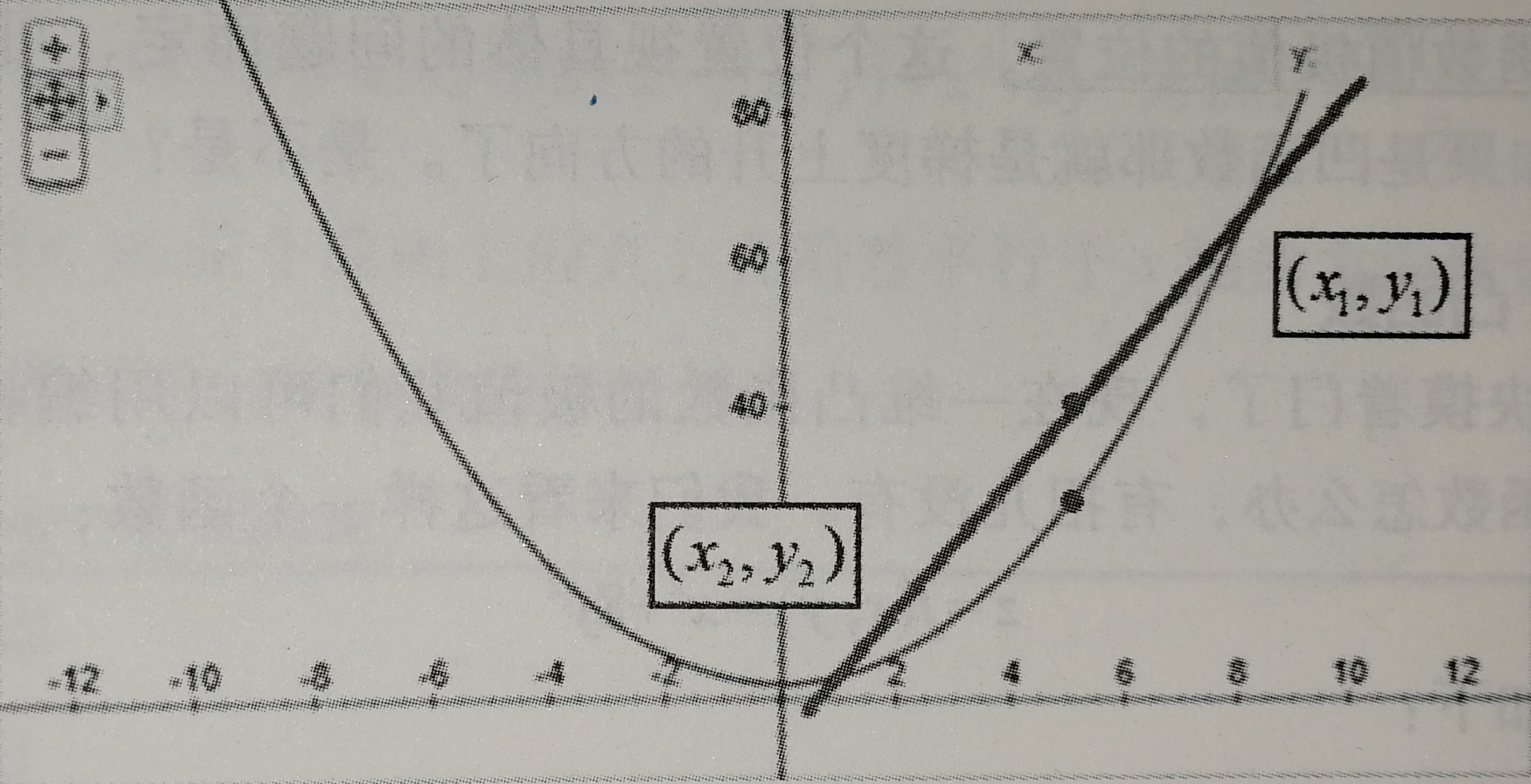
如图所示，当$x_n=3$时，$-\eta\frac{f(x)}{dx}$为负数，更新后$x_{n+1}$会减小；当$x_n=-3$时，$-\eta\frac{f(x)}{dx}$为正数，更新后$x_{n+1}$还是会减小。这总函数其实就是凸函数。满足$f(\frac{x_i+x_2}{2})=\frac{f(x_i)+f(x_2)}{2}$都是凸函数。沿着梯度的方向是下降最快的。

　　我们初始化$(w_0,b_0,Loss_o)$后下一步就水到渠成了，

$$w_1=w_o-\eta \frac{\partial Loss}{\partial w},b_1=b_o-\eta \frac{\partial Loss}{\partial b}$$

　　有了梯度和学习率的$\eta$乘积之后，当这个点逐渐接近“碗底”的时候，偏导也随之下降，移动步伐也会慢慢变小，收敛会更为平缓，不会轻易出现“步子太大”而越过最低的情况。一轮一轮迭代，直到每次更新的值非常小，损失值不在减小就可以判断为训练结束，此时得到的(w,b)就是我们要求的模型。

神经网络的训练

　　哈哈哈，是不是发现我刚才讲的明明是线性回归模型的训练，和大家想知道的神经网络的训练有毛线关系呀！你们说的没错，就是有一毛钱的关系，嘿嘿[笑脸]！

这个网络用函数表达式写的话如下所示：

第一层(隐藏层)　　$\begin{matrix}z_h=w_nx+b_n,&y_h=\frac{1}{1+e^{-z_h}}\end{matrix}$

第二层(输出层)　　$\begin{matrix}z_o=w_oy_h+b_o,&y_o=\frac{1}{1+e^{-z_o}}\end{matrix}$

接下来的工作就是把$w_h、b_h、w_o、b_o$参数利用梯度下降算法求出来，把损失函数降低到最小，那么我们的模型就训练出来呢。

第一步：准备样本，每一个样本$x_i$对应标签$y_i$。

第二步：清洗数据，清洗数据的目的是为了帮助网络更高效、更准确地做好分类。

第三步：开始训练，

$Loss=\sum_{i=1}^{n}(y_{oi}-y_i)^2$

我们用这四个表达式，来更新参数。

$$(w_h)^n=(w_h)^{n-1}-\eta \frac{\partial Loss}{\partial w_h}$$

$$(b_h)^n=(b_h)^{n-1}-\eta \frac{\partial Loss}{\partial b_h}$$

$$(w_o)^n=(w_o)^{n-1}-\eta \frac{\partial Loss}{\partial w_o}$$

$$(b_o)^n=(b_o)^{n-1}-\eta \frac{\partial Loss}{\partial b_o}$$

问题来了，$\frac{\partial Loss}{\partial w_h}$、$\frac{\partial Loss}{\partial b_h}$、$\frac{\partial Loss}{\partial w_o}$、$\frac{\partial Loss}{\partial b_o}$这4个值怎么求呢？

$$Loss=\sum_{i=1}^{n}(y_{oi}-y_i)^2\Rightarrow Loss=\frac{1}{2}\sum_{i=1}^{n}(y_{oi}-y_i)^2$$

配一个$\frac{1}{2}$出来，为了后面方便化简。

$$\frac{\partial Loss}{\partial w_h}=\frac{\partial \sum_{i=1}^{n}(y_{oi}-y_i)^2}{\partial w_o}=\frac{\partial \sum_{i=1}^{n}y_{oi}}{w_o}=\sum_{i=1}^{n}\frac{\partial y_{oi}}{\partial z_o}·\frac{z_o}{w_o}=\sum_{i=1}^{n}\frac{\partial y_{oi}}{\partial z_o}·\frac{z_o}{y_h}·\frac{\partial y_h}{\partial z_h}·\frac{\partial z_h}{\partial w_h}$$

其他三个参数，和上面类似，这是一种“练乘型”求导方式。我们的网络两层就4个连乘，如果是10层，那么就是20个连乘。但一层网络的其中一个节点连接着下一层的其他节点时，那么这个节点上的系数的偏导就会通过多个路径传播过去，从而形成“嵌套型关系”。

DropOut

　　DropOut是深度学习中常用的方法，主要是为了克服过拟合的现象。全连接网络极高的VC维，使得它的记忆能力非常强，甚至把一下无关紧要的细枝末节都记住，一来使得网络的参数过多过大，二来这样训练出来的模型容易过拟合。

　　DropOut：是指在在一轮训练阶段临时关闭一部分网络节点。让这些关闭的节点相当去去掉。如下图所示去掉虚线圆和虚线，原则上是去掉的神经元是随机的。

python代码实现MNIST手写数字识别

　　哈哈哈哈....这次作者终于要写代码了，是的这次我一定写，emmmm，虽然现在以及11.35了，但是我还是要坚持把代码写完。

　　我们开看看我们上面学的全连接神经网络到底能做什么——手写数字识别。

MNIST是一个由美国由美国邮政系统开发的手写数字识别数据集。手写内容是0~9，一共有60000个图片样本，我们可以到MNIST官网免费下载，这官网的网页做的好粗糙呀，一点都没有国际型大网站的样子，可能国外主办方认为我把核心的东西给你讲了就行了，好不好看我不管。总共4个文件，该文件是二进制内容。

train-images-idx3-ubyte.gz:  training set images (9912422 bytes)   图片样本，用来训练模型
train-labels-idx1-ubyte.gz:  training set labels (28881 bytes) 　　 图片样本对应的数字标签
t10k-images-idx3-ubyte.gz:   test set images (1648877 bytes) 　　  测试样本
t10k-labels-idx1-ubyte.gz:   test set labels (4542 bytes)　　　　　　测试样本对应的数字标签

我们下载下来的文件是.gz后缀的，表明是一个压缩文件，我们设计代码的时候，需要考虑对文件进行解压。

使用tensorFlow完成实验

这段代码在TensorFlow官网的Github上面也是有的，地址：https://github.com/tensorflow/tensorflow，文件目录在：tensorflow/tensorflow/examples/tutorials/mnist