关于GCD的几个结论

设a和b的最大公约数是d，那么：

1. d是用sa+tb（s和t都是整数）能够表示的最小正整数

　　证明：设x=sa+tb是sa+tb能够表示出的最小正整数。首先，有d|x，证明如下：

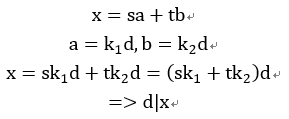
　　　　因此有x>=d，现在只要证明x是公约数，就可以证明x就是这个最大公约数了。只需证明x|a且x|b。

　　　　先证x|a。设a=qx+r（q是自然数，0<=r<x），那么r=a-qx=a-q(sa+tb)=(1-qs)a+(-qt)b。可以看出r也满足Sa+Tb这种形式，假如r也是正整数的话，r<x，那么与x是Sa+Tb这种形式的最小正整数矛盾。因此假设不成立，r不是正整数。所以r=0。所以有x|a。

　　　　证x|b同理。

　　所以命题得证。有结论：存在整数s,t使得sa+tb=d，其中d=gcd(a,b)。并且d是形如sa+tb的所有正整数里最小的。

2. c是a和b的公约数，那么c|d

　　证明：由命题1，存在整数s,t，使得sa+tb=d。由于a=pc，b=qc（p,q都是正整数），所以d=spc+tqc=(sp+tq)c。所以c|d。

　　所以命题得证。有结论：任何公约数都整除最大公约数。

3. 如果c|d，那么有c|a且c|b

　　证明：显然有d|a且d|b。由整除的传递性，就有c|a且c|b。

　　由命题2和命题3得出推论：一个数整除最大公约数，跟这个数分别整除这两个数是等价的条件。

　　这是今天在看莫比乌斯反演的时候有一步转化没有看懂，就在这里推了一下。