HDU - 4336：Card Collector（min-max容斥求期望）

In your childhood, do you crazy for collecting the beautiful cards in the snacks? They said that, for example, if you collect all the 108 people in the famous novel Water Margin, you will win an amazing award.

As a smart boy, you notice that to win the award, you must buy much more snacks than it seems to be. To convince your friends not to waste money any more, you should find the expected number of snacks one should buy to collect a full suit of cards.

InputThe first line of each test case contains one integer N (1 <= N <= 20), indicating the number of different cards you need the collect. The second line contains N numbers p1, p2, ..., pN, (p1 + p2 + ... + pN <= 1), indicating the possibility of each card to appear in a bag of snacks.

Note there is at most one card in a bag of snacks. And it is possible that there is nothing in the bag.OutputOutput one number for each test case, indicating the expected number of bags to buy to collect all the N different cards.

You will get accepted if the difference between your answer and the standard answer is no more that 10^-4.Sample Input

1
0.1
2
0.1 0.4

Sample Output

10.000
10.500

题意：题面不好看，题意很简单，就是给定S个物品，然后每次取到物品i的概率为pi，∑pi<=1; 求把所有物品都至少取到一次的期望。

思路：有一个专门这样的算法，叫min-max容斥。 他解决问题的方式：假设有S个对象，求把所有东西都取到的期望，不直接求，而是通过求子集的期望，然后容斥得到结果。   T是S的子集，我们得到每个子集T的期望，然后乘上容斥系数，累加起来就是答案。 假设我们dfs得到了S的子集T，并且得到至少取到这个子集的一个的概率p，则其期望为1/p；

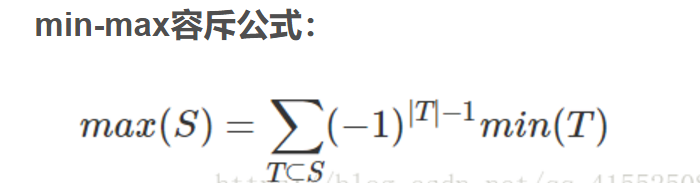
#include<bits/stdc++.h>
using namespace std;
const int maxn=;
double p[maxn],ans; int N;
void dfs(int pos,double now,int opt)
{
    if(pos==N+) {
        if(opt>){
           if(opt&) ans+=1.0/now;
           else ans-=1.0/now;
        }
        return ;
    }
    dfs(pos+,now,opt);
    dfs(pos+,now+p[pos],opt+);
}
int main()
{
    while(~scanf("%d",&N)){
        for(int i=;i<=N;i++) scanf("%lf",&p[i]);
        ans=; dfs(,0.0,);
        printf("%.4lf\n",ans);
    }
    return ;
}