「BZOJ 4289」 PA2012 Tax

「BZOJ 4289」 PA2012 Tax

题目描述

给出一个 \(N\) 个点 \(M\) 条边的无向图，经过一个点的代价是进入和离开这个点的两条边的边权的较大值，求从起点 \(1\) 到点 \(N\) 的最小代价。起点的代价是离开起点的边的边权，终点的代价是进入终点的边的边权

\(N \leq 10^5, M \leq 2 \times 10^5\)

### 解题思路 :

首先考虑一个暴力的做法，建一个新图，把每一条边看成新图的一个点‘

对于原图的每一个点 \(u\) 对于边 \((u, x), (u, y)\) 在新图中连边 \((u, x) \rightarrow (u, y) = \max(val_{(u, x)}, val_{(u, y)})\)

这样做的复杂度是 \(O(\sum deg_u^2 logn)\)，一个菊花图就 \(TLE\) 了

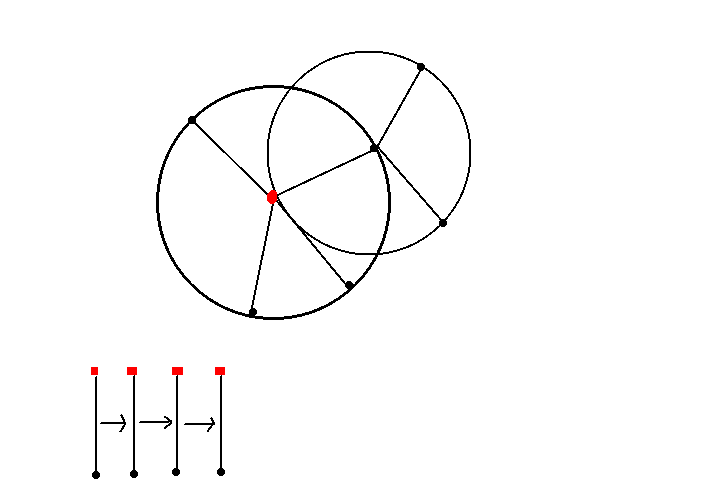
考虑简化新图的边数，不妨观察新图的是怎么得到的

对于原图的一个点，所有与其相邻的连的边在新图都两两连边，其表示从一条边进这个点，从一条边出这个点，边权是两条边的 \(\max\)

观察发现，虽然原图一个点在新图中能产生的边多达 \(deg^2\) 条，但是边的权值只有最多 \(deg\) 种

不妨对原图一个点周围的边按照权值从小到大排序，相邻两条边连一条 \(i \rightarrow i+1\) 的有向边，权值为 \(val_{i+1} - val_i\)

那么从一条较小的边进去，从一条较大的边出来的话，一路经过的权值和恰好等于较大的边的权值

但是可能是从较大的边进入一个点，同时判断走这条边是否真的离开了这个点也很困难，于是就需要分类讨论了

观察发现，可以把一个点周围的边按照权值排序后看成一个环，答案的形态就是从一个环经过一些环内的边再通过一条环边到达另外一个环，以此反复

那么不妨把新图的一个点拆成两个点，\(u\) 表示这个点此时属于原图编号较小的点对应的环， \(u'\) 表示属于原图编号较大的点对应的环

考虑每当从一个环进到另外一个环时，设一个初始权值 $x $ 等于入环的边的边权，如果 \(x\) 是较小的边，那么沿着边权为 \(val_{i+1} - val_i\) 的有向边出环，否则就走边权为 \(0\) 的有向边出环，这样保证了出环时的权值正确

所以只需要对于每个点的相连边按照权值排序后，从小到大相邻的点连 \(val_i+1 - val_i\) 的有向边，从大到小连边为 \(0\) 的有向边，然后在出环的时候 \(u\) 和 \(u'\) 连一条权值为 \(val_u\) 的无向边即可，这样点数是 \(O(2m)\)，边数是 \(O(3m)\)

注意要保证同一个环内连的边其对应的端点是同一个，而不是全都是 \(u\) 或 \(u'\) ，剩余的只需要跑一遍 \(Dijkstra\) 即可

复杂度是\(O(mlogm)\)

/*program by mangoyang*/
#include<bits/stdc++.h>
#define inf ((ll) (1e18))
#define Max(a, b) ((a) > (b) ? (a) : (b))
#define Min(a, b) ((a) < (b) ? (a) : (b))
typedef long long ll;
using namespace std;
template <class T>
inline void read(T &x){
	int f = 0, ch = 0; x = 0;
	for(; !isdigit(ch); ch = getchar()) if(ch == '-') f = 1;
	for(; isdigit(ch); ch = getchar()) x = x * 10 + ch - 48;
	if(f) x = -x;
}
#define int ll

const int N = 2000005;
int a[N], b[N], nxt[N], head[N], cnt;
int dis[N], n, m;

struct Edge{
	int id, x, y, val;
	inline int bel(int u){ return (int)(min(x, y) == u); }
}; vector<Edge> g[N];
inline bool cmp(Edge A, Edge B){ return A.val < B.val; }
inline void add(int x, int y, int z){
	a[++cnt] = y, b[cnt] = z, nxt[cnt] = head[x], head[x] = cnt;
}
inline void Addedge(int u){
// x + m表示边 x 挂在编号较小的点围成的环上所产生的节点
// x 表示边 x 挂在编号较大的点围城的环上所产生的节点
// 同编号环(x -> y) 小到大 val = y.val - x.val
// 同编号环(x -> y) 大到小 val = 0
// 异编号环(x -> y) 小到大/大到小 val = y.val
	sort(g[u].begin(), g[u].end(), cmp);
	for(int i = 0, x, y; i < g[u].size(); i++){
		if(i){
			x = g[u][i].id + g[u][i].bel(u) * m;
			y = g[u][i-1].id + g[u][i-1].bel(u) * m;
			add(x, y, 0);
		}
		if(i < g[u].size() - 1){
			x = g[u][i].id + g[u][i].bel(u) * m;
			y = g[u][i+1].id + g[u][i+1].bel(u) * m;
			add(x, y, g[u][i+1].val - g[u][i].val);
		}
		x = g[u][i].id + g[u][i].bel(u) * m;
		y = g[u][i].id + (g[u][i].bel(u) ^ 1) * m;
		add(x, y, g[u][i].val);
	}
}

struct Node{
	int d, id;
	bool operator < (const Node &A) const{ return d > A.d; }
}; priority_queue<Node> pq;
inline void Dijkstra(int S){
	for(int i = 0; i <= 2 * m + 1; i++) dis[i] = inf / 3;
	pq.push((Node){0, S}), dis[S] = 0;
	while(!pq.empty()){
		Node now = pq.top(); pq.pop();
		int u = now.id;
		if(dis[u] != now.d) continue;
		if(u == 2 * m + 1) return;
		for(int p = head[u]; p; p = nxt[p]){
			int v = a[p];
			if(dis[v] > dis[u] + b[p])
				dis[v] = dis[u] + b[p], pq.push((Node){dis[v], v});
		}
	}
}

signed main(){
	read(n), read(m);
	for(int i = 1, x, y, z; i <= m; i++){
		read(x), read(y), read(z);
		g[x].push_back((Edge){i, x, y, z});
		g[y].push_back((Edge){i, y, x, z});
	}
	for(int i = 1; i <= n; i++) Addedge(i);
	for(int i = 0; i < g[1].size(); i++) add(0, g[1][i].id + m, g[1][i].val);
	for(int i = 0; i < g[n].size(); i++) add(g[n][i].id, 2 * m + 1, 0);
	Dijkstra(0), cout << dis[2*m+1];
	return 0;
}