BERT模型总结
BERT模型总结
前言
BERT是在Google论文《BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding》中被提出的,是一个面向NLP的无监督预训练模型,并在多达11个任务上取得了优秀的结果。这个模型的最大意义是使得NLP任务可以向CV一样使用与训练模型,这极大的方便了一个新的任务开始,因为在NLP领域,海量数据的获取还是有难度的。
模型概述:BERT是一个无监督的NLP与训练模型,结构上是Transformer的编码部分,每个block主要由多头self-Attention、标准化(Norm)、残差连接、Feed Fordawrd组成。在具体任务中,主要分为模型预训练和模型微调两个阶段。在模型预训练阶段,因为模型参数巨大,通常是上千万乃至上亿的数量级,所以需要大量的数据训练,所幸这时候模型是无监督的,只需要爬取或使用开源数据集即可;在模型微调阶段,需要针对具体的任务来微调模型,已达到较好的效果。
1. 模型整体结构
Bert就是Transformer的编码部分,下图是Transformer的具体结构:
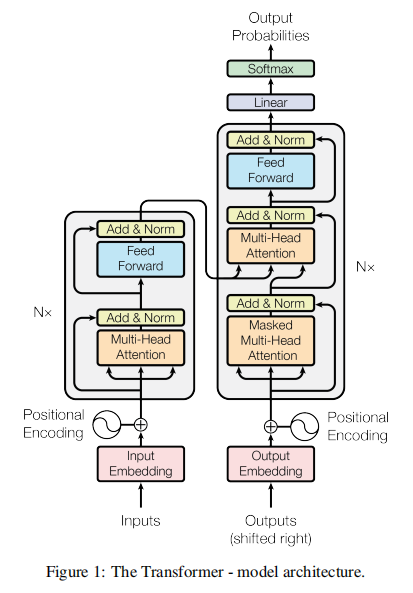
上图左侧为Transformer的编码部分,右侧为Transformer的解码部分,本文主要以编码部分详细讲解Bert的结构。左侧的编码部分包括输入,添加位置编码,以self-Attention、Add&Norm、Feed Fordward的block。下面就每个具体细节进行具体分析。
2. 位置编码
位置编码是用来捕获文本之间的时序关联性的,例如打开现在热度第一的新闻的第一句话:“重庆主城区一栋30层的居民楼发生大火,造成百余名群众被困,重庆市政府迅速调集消防、公安、卫生等数百名人员赶赴现场施救。”其中,“重庆市”与“主城区”相关度最高,位置最近。当对NLP文本处理时,位置更近的文本一般相关性更大,所以将位置编码融入到数据中是很有必要的。需要要说明的是与Bert这种全部基于Attention不同的是,之前基于RNN的模型在模型结构上已经可以将这种时序信息考虑在内。
在具体处理方式上,采用的是Embedding+Positional的方法,将数据之间的关联性融入到数据中。Embedding是嵌入到相应维度的文本数据,Positional在论文中使用了\(sine\)和\(cosine\)函数的线性变换来提供模型的位置信息,公式如下:
\]
那为何加了位置编码就能获取数据间位置的特征呢?在self-attention的结构中,在对每维数据计算权重时,是采用点积的形式,本质上就是计算向量之间的相关性。而位置编码将临近的数据加上频率接近的位置编码,就是增加了相邻数据的相关性。下图是位置编码向量的热图,可以看出距离越近,频率就更加接近。
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAAkQAAAJcCAYAAAAYZbusAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzs3XmYXVWVsPF3JSGEMM8CiQYQUBohakAUEQRRtBl6QBSFL8wqH7SCiNDaoratNNjQdGtjpwMCSsugIKig8tkijcosyDyKEAgEZDAQyFTr++OeCjeVW1W3kjr73qTen899Uvfcc85aVUZrZ5+194rMRJIkaSQb1ekEJEmSOs0BkSRJGvEcEEmSpBHPAZEkSRrxHBBJkqQRzwGRJEka8RwQSTWIiI9GxM87GP+1EfFiRIzu5/MvRsR327zXuRHxleHNcPgM9r1KUjscEElLKSLeGRG/iYgXIuLZiPh1RGwPkJkXZOZ7O5VbZj6amatl5sI640TEwRGxsBqQ9L6+UXPMRyLiPb3vS32vklZsYzqdgLQ8iog1gB8DnwAuBsYCOwNzO5lXh/w2M9/Z6SQkaVk4QyQtnS0BMvN7mbkwM1/OzJ9n5u9h0czJdb0nR0RGxMcj4oGIeC4ivhkRUX222OOriJhUnT+m6V4PR8TsiPhDRHy0Oj4qIj4fEX+MiFkRcX5ErNnPPTaNiF9V97gaWK/5m4mISyLiyWq269qI+Itl/QFFxDURcXjT+7Z/JtXnR0TEPVXOd0fEWyLiO8BrgR9Vs1EntPheN46IK6pZuwcj4oime34xIi6uflazI+KuiJiyrN+rpOWfAyJp6dwPLIyI8yLi/RGxdhvX7AVsD2wH7A+8b7ALImJV4N+A92fm6sA7gNuqjw+uXu8GNgNWA/p7XPXfwC00BkL/CEzt8/lVwBbABsCtwAVtfD/DoeXPJCI+CHwR+D/AGsA+wJ8y8yDgUWDv6jHZqS3u+T1gBrAxsB/w1YjYvenzfYALgbWAK+j/ZyZpBHFAJC2FzPwz8E4ggf8Cnq5mJTYc4LJTMvP5zHwU+CUwuc1wPcA2EbFKZs7MzLuq4x8FTs/MhzPzReAk4MO9MyW9IuK1NAYd/5CZczPzWuBHfb6fczJzdmbOpTEQ2a53tqkNO0bE802vHdu8Dvr/mRwOnJqZN2XDg5n5x8FuFhETafz38tnMfCUzbwOmAwc1nXZdZl5Z1Rx9h8ZgTNII54BIWkqZeU9mHpyZE4BtaMxI/OsAlzzZ9PUcGjM6g8V4CfgQ8HFgZkT8JCLeUH28MdA8SPgjjbrAvoOyjYHnqns1nwtARIyOiFMi4qGI+DPwSPXRYo/VBnB9Zq7V9Lq+zeug/5/JROChIdyn18bAs5k5u+nYH4FNBog5ru8gUtLI44BIGgaZeS9wLo2B0VC9BIxvev+aPvf+WWbuAWwE3EtjRgrgCeB1Tae+FlgAPNXn/jOBtavHb83n9voIsC/wHmBNYFJ1PFg2A35fg3gM2Lyfz3KA654A1omI1ZuOvRZ4fAixJY1ADoikpRARb4iIT0fEhOr9ROAAYCizI71uA95V7aezJo1HX71xNoyIfarBzFzgRaB3efn3gGOrgunVgK8CF2XmguabV4+abga+FBFjI+KdwN5Np6xe3ftPNAYwX12K76G/7+tvImJ8RLweOGwI104Hjo+It0bD6yOid/D3FI2aqSVk5mPAb4CvRcS4iNi2iluqJkrScsoBkbR0ZgNvA26IiJdoDITuBD491Btl5tXARcDvaRQ+/7jp41HVPZ8AngV2AY6qPjuHRg3MtcAfgFeAY/oJ85Eq32eBk4Hzmz47n8ZjpceBu1m6QV0rZwDzaAxgzmMIg5LMvAT4JxrF4LOBHwLrVB9/Dfh8Va90fIvLD6Axy/UEcBlwcvUzlqR+ReZAs8+SJEkrPmeIJEnSiOeASJIkjXgOiCRJ0ojngEiSJI14HdmMLCL2BM4ERgPTM/OUgc6/aZO/tvJbkjRibP/4Zcu6D9iQzH/m4WK/Z1dab7Oi31u7is8QRcRo4JvA+4GtgQMiYuvSeUiSJPXqxCOzHYAHq/5L82g0Wdy3A3lIkiQBnRkQbUJjW/5eM1i8zxAAEXFkRNwcETdf9tIjpXKTJGnk6VlY7tWlOjEgavXscIlnl5k5LTOnZOaUv151Uv1ZSZKkEasTRdUzaHSy7jWBxhb7/XrTjw6pNaFmo9Z/3eAnDaNH33dC0Xivu/asovHuePOxReO96XdnFI13++Tjisbb7rbTi8Zbkb+/Ffl7A7htuyF3kVkmk2//l6LxVvTvr7js6XQGHdeJGaKbgC2qhpRjgQ8DV3QgD0mSJKADM0SZuSAijgZ+RmPZ/TmZeVfpPCRJUqXHGaKO7EOUmVcCV3YitiRJUl8dGRBJkqTukdYQ2bpDkiSp+AxRREwEzgdeA/QA0zLzzAGvWX29EqkB0PP4vcViAay+wdyi8UqLrtygXZK0GGuIOvLIbAHw6cy8NSJWB26JiKsz8+4O5CJJktSRVWYzgZnV17Mj4h4aO1U7IJIkqROsIepsDVFETALeDNzQ4rNFrTumX3h56dQkSdII0rFVZhGxGvAD4FOZ+ee+n2fmNGAawNwHfrNEaw9JkqTh0pEBUUSsRGMwdEFmXjrY+U8d8A/1J1VZ78hti8UCWHnDFbvqOMKxrCR1vS5uulpK8UdmERHA2cA9mVm2uY8kSVILnZgh2gk4CLgjIm6rjv19tXu1JEkqzaLqjqwyuw5YsZ8TSZKk5YqtOyRJGuncmHH5GBDtPePlYrF+9cvbBj9pGI3ecNWi8UoXzo0eZVG1utN2t53O7ZOP63QakrpEJ5fdjwZuBh7PzL06lYekkcnBkPQqm7t2dmPGTwL3dDC+JEkS0KEBUURMAP4SmN6J+JIkqUlPT7lXl+rUDNG/AifQ6HbfUnPrjj/NeapcZpIkacTpxMaMewGzMvOWgc7LzGmZOSUzp6w7fsNC2UmSNAJlT7lXl+rUxoz7RMQHgHHAGhHx3cw8sL8L7n/h8WLJ3fertxaLBbDNUeOLxivN1h1SZ/i/PWloOrEx40nASQARsStw/ECDIUmSVDN7mXV0lZkkSVJX6OjGjJl5DXBNJ3OQJGnE6+LanlKcIZIkSSPectG645T1dy4W638Kt51907prlw1Y+F8BoyzslCQtBzoyIIqItWhsyrgNkMChmfnbTuQiSdKI18UbJpbSqRmiM4GfZuZ+ETEWWLHXnkuSpK5WfEAUEWsA7wIOBsjMecC80nlIkqSKRdUdKareDHga+HZE/C4ipkfEqn1Pam7d8ZsXHyifpSRJGjE6MSAaA7wFOCsz3wy8BJzY96Tm1h3vWG2L0jlKkjRy2Ny1IzVEM4AZmXlD9f77tBgQNTvy61vWnlSv/Y+/sVgsgE+ttXnReKX/MsYoV5lJkrpfJ1p3PBkRj0XEVpl5H7A7cHfpPCRJUkOmrTs6tcrsGOCCaoXZw8AhHcpDkiSpMwOizLwNmNKJ2JIkqQ9Xmdm6Q5IkqVM7VR8LHE5jl+o7gEMy85X+zh+z6wGlUuPuOT8sFguANd5TNFyWbt0xesUuqrY1iaQVQhev/iql+AxRRGwC/B0wJTO3AUYDHy6dhyRJUq9OFVWPAVaJiPk02nY80aE8JEmSNUTlZ4gy83Hg68CjwEzghcz8ed/zmneqnn7+haXTlCRJI0gnepmtDewLbAo8D1wSEQdm5nebz8vMacA0gPmzHrBQQ5KkuvS4D1EnVpm9B/hDZj6dmfOBS4F3dCAPSZIkoDM1RI8CO0bEeOBlGjtV3zzQBXNPPb5EXgA88dKfisUCiDXWLRqveOsOV2FJkpYDnWjdcUNEfB+4FVgA/I7q0ZgkSeoAi6o7tlP1ycDJnYgtSZLUlztVS5I00vX0lHu1ISL2jIj7IuLBiDixxeevjYhfRsTvIuL3EfGBZf0ROCCSJEldIyJGA98E3g9sDRwQEVv3Oe3zwMWZ+WYamzv/x7LGre2RWUScA+wFzKp2pCYi1gEuAiYBjwD7Z+Zzg93riEuirjSXMH/hgmKxAFh1zbLxSrfusKhakrpfd9UQ7QA8mJkPA0TEhTS267m76ZwE1qi+XpNh2OC5zhmic4E9+xw7EfhFZm4B/KJ6L0mSRojmjZer15F9TtkEeKzp/YzqWLMvAgdGxAzgSuCYZc2rthmizLw2Iib1ObwvsGv19XnANcBn68pBkiS1oeCWLM0bL/ej1WOhvo8bDgDOzcx/iYi3A9+JiG1yGTqYl64h2jAzZwJUf27Q34nNI8gHX3ykVH6SJKmzZgATm95PYMlHYocBFwNk5m+BccB6yxK0a4uqM3NaZk7JzCmvX21Sp9ORJGnF1V2rzG4CtoiITSNiLI2i6Sv6nPMojY2diYg30hgQPb0sP4LS+xA9FREbZebMiNgImNXORZfMvKnmtBY3bszYovFifOHC6sI9a0aNtrBaktSezFwQEUcDPwNGA+dk5l0R8WXg5sy8Avg08F8RcSyNx2kHZ+Yy/bIpPSC6ApgKnFL9eXnh+INyMDS8HAxJUvfL7K7mrpl5JY1i6eZjX2j6+m5gp+GMWdsjs4j4HvBbYKuImBERh9EYCO0REQ8Ae1TvJUmSOqrOVWYH9PPR7nXFlCRJS6Fw4+9u1LVF1ZIkSaV0pLmrJEnqIt21U3VHlG7dcRqwNzAPeAg4JDOfH+xe+2+0Q11pLuHWl2cUiwUQ41YtGo/CrUlilEXVkqTuV7p1x9XANpm5LXA/cFKN8SVJktpStHVHZv686e31wH51xZckSW2yqLqjRdWHAlf196GtOyRJUikdGRBFxOeABcAF/Z1j6w5JkgrJnnKvLlV8lVlETKVRbL17u9tsT9u/3pyaHXzxRuWCAYxdpWi4fHl20XjRqmexJEldpuiAKCL2BD4L7JKZc0rGliRJ/bCGqHjrjm8AqwNXR8RtEfGtuuJLkiS1q3TrjrPriidJkpZSF9f2lGLrDkmSNOLZukOSpJHOGqKyrTuaPjseOA1YPzOfGexeK3/m1HqSbGGni75ULBZAjBlbNF7aukOSpCWUbt1BREwE9gAerTG2JElqV09PuVeXqm1AlJnXAs+2+OgM4ATAqQNJktQVihZVR8Q+wOOZeXsb5y5q3TH9/AsLZCdJ0gjlTtXliqojYjzwOeC97ZyfmdOAaQDzZz3gbJIkSapNyVVmmwObArdHo5/DBODWiNghM58c6MIFv/zvAuk1vDv+XCwWAKNGl423cH7RcKNGO5aVpK7XxbU9pRQbEGXmHcAGve8j4hFgSjurzCRJkupUunWHJElS1ynduqP580l1xZYkSUPQxcXOpdi6Q5IkjXi27pAkaaSzqLp8646IOAY4GlgA/CQzTxjsXt/6zAN1pbmEw/Z4uVisjrB1x7BqLJiUJC3v6pwhOhf4BnB+74GIeDewL7BtZs6NiA36uVaSJJViDVHx1h2fAE7JzLnVObPqii9JktSu0kXVWwI7R8QNEfGriNi+vxObW3f89sVyj8wkSRpxbO5afEA0Blgb2BH4DHBxROsqjMyclplTMnPK21fbomSOkiRphCm9ymwGcGlmJnBjRPQA6wFPD3TRSbOuLZEbAB9/10eKxQKgZ2HRcFm4dUe4sYMkdb8unrkppfSvqx8CuwFExJbAWMDWHZIkqaPqXHb/PWBXYL2ImAGcDJwDnBMRdwLzgKnVbJEkSeoUfxV3pHXHgXXFlCRJWhruVC1J0khnDZG9zCRJkoq27oiIycC3gHE0WncclZk3DnavrdaaUFeaS4htdiwWCyjeSqN4647wubQkdT1niGqdIToX2LPPsVOBL2XmZOAL1XtJkqSOqrOo+tqImNT3MLBG9fWawBN1xZckSW2yl1nxoupPAT+LiK/TmJ16R38nRsSRwJEAm6y+GeuO37BMhpIkacQpXVT9CeDYzJwIHAuc3d+Jza07HAxJkqQ6lZ4hmgp8svr6EmB6Oxf9eOIqtSXU16iNyvZNywXzisajcOuOUWMsqpakrmdRdfEZoieAXaqvdwNsYy9JkjqudOuOI4AzI2IM8ApVjZAkSeogW3d0pHXHW+uKKUmStDRs3SFJ0khnDdHyMSDa4L//sVisGFuugBug57kni8YrvlO1zWEkScuB2n5dRcTEiPhlRNwTEXdFxCer4+tExNUR8UD159p15SBJktrQ01Pu1aXq/Pf7AuDTmflGYEfg/0bE1sCJwC8ycwvgF9V7SZKkjqmzqHomMLP6enZE3ANsAuxLY/UZwHnANcBn68pDkiQNwtYdZfYhqnqavRm4AdiwGiz1Dpo26OeaIyPi5oi4efqFl5dIU5IkjVC1F1VHxGrAD4BPZeafI6Kt6zJzGjANYO4Dv3GDBEmSapI9/pqtdUAUESvRGAxdkJmXVoefioiNMnNmRGwEzBrsPjn7mTrTXDzWSmOLxQLg5dll480v3Cok/B+ZJKn71bnKLGg0b70nM09v+ugKGj3NqP70eZgkSZ3kKrNaZ4h2Ag4C7oiI26pjfw+cAlwcEYcBjwIfrDEHSZKkQdW5yuw6oL+Cod3riitJkobIVWbFu91LkiR1neWidcfte51bLNZ2F/11sVgAFC7izoXzi8azdYckaXnQidYdp0XEvRHx+4i4LCLWqisHSZLUhp4s9+pSnWjdcTWwTWZuC9wPnFRjDpIkSYMq3rojM3/edNr1wH515SBJktrQxcvhS+lE645mhwJX9XPNotYdP5zzh3oTlCRJI1rx1h1Nxz9H47HaBa2ua27dccPGf9O9Dx0lSVreOUPUkdYdRMRUYC9g98wcdLDzwVceqC/JPu697bfFYgHEG7ctGq+0UcvFOkZJ0khX26+r/lp3RMSewGeBXTJzTl3xJUlSmwafm1jhdaJ1x78BKwNXN8ZMXJ+ZH68xD0mSpAF1onXHlXXFlCRJS8EaIlt3SJIk1VlDNBE4H3gN0ANMy8wzmz4/HjgNWD8znxnoXnMWzK0rzSW88v/uKhYLYJVNJhSNxyqrlY23gg+5I3zuLmkF0MU7SJdSZw1R707Vt0bE6sAtEXF1Zt5dDZb2AB6tMb4kSVJbavv3e2bOzMxbq69nA/cAm1QfnwGcADgklSSp07Kn3KtLFd+pOiL2AR7PzNsHuWbRTtWvzHuhQJaSJGmkKrpTNY3HaJ8D3jvYdc07Va+3xpbOJEmSVBdriOqdIWqxU/XmwKbA7RHxCDABuDUiXlNnHpIkSQMpulN1Zt4BbNB0ziPAlMFWmZ09fkpdaS7hzhvmF4sFsP0+zxaNx9hxRcPFCr7KTJK0Yii+U3VmujGjJEldJN2YsSM7VTefM6mu+JIkSe2yF7kkSSOdRdUr+j7CkiRJg+tI646IOAY4msYy/J9k5gkD3eu939utrjSX8LVDflksFsCUZ8sWVcc66xWN55BbkpYDXbxhYinFW3cAGwL7Attm5tyI2GDAu0iSJNWszqLqmcDM6uvZEdHbuuMI4JTMnFt9NquuHCRJUhusISrfugPYEtg5Im6IiF9FxPb9XLOodcfZP762RJqSJGmEKtq6IzP/HBFjgLWBHYHtgYsjYrPMXGx42ty64+VfTnfoKklSXdyHqN4BUYvWHQAzgEurAdCNEdEDrAc83d99Rm/xtjrTXMwNC39QLBZAzzOrFI03+nXzisYLN3ZQl9ruttO5ffJxnU5DUpco2rqj8kNgN+CaiNgSGAsM2LpDkoabgyGpiTVE5Vt3AOcA50TEncA8YGrfx2WSJEkldap1x4F1xZUkSUPkPkRumydJkmTJqyRJI501ROVbd0TEZOBbwDgau1kflZk3DnSvF485uq40l3DvnOeKxQJYOKvsRt2j588vGi9G9ffUVJKk7tGJ1h2nAl/KzKsi4gPV+11rzEOSJGlAnWjdkcAa1WlrAk/UlYMkSRpcujFjR1p3fAo4LSIeA74OnNTPNYtad5z3yMwSaUqSpBGq9gFR39YdwCeAYzNzInAsjc0bl5CZ0zJzSmZOmTppo7rTlCRp5OrJcq8u1YnWHVOBT1ZfXwJMH+w+f3vT2HoSbOGpl54vFgtg/pNrF403dt7covHc2EGStDzoROuOJ4BdgGtotPB4oK4cJElSG7p45qaUTrTuOAI4s+p6/wpwZI05SJIkDapTrTveWldcSZI0RF3WuiMi9gTOBEYD0zPzlH7O249G+c32mXnzssS0wkOSJHWNiBgNfBN4P7A1cEBEbN3ivNWBv6Oxgn2ZOSCSJGmk665VZjsAD2bmw5k5D7gQ2LfFef9IY3PnV4bjR1BnUfU44Fpg5SrO9zPz5IjYlMY3tw5wK3BQ9Q3367pZd9eV5hJKl5XNebpsO7nxtu6QJHVQRBzJ4vXD0zJzWtP7TYDHmt7PAN7W5x5vBiZm5o8j4vjhyKvO38Zzgd0y88Vq+f11EXEVcBxwRmZeGBHfAg4DzqoxD0mSNIAsuMqsGvxMG+CUVv+SXpRgRIwCzgAOHs68antklg0vVm9Xql5JY6n996vj5wF/VVcOkiRpuTMDmNj0fgKLt/laHdgGuCYiHgF2BK6IiCnLErTujRlHA7cAr6dRIPUQ8HxmLqhOmUFjaqzVtYum1EaNXpNRo1atM1VJkkau7tqH6CZgi6rE5nHgw8BHej/MzBeA9XrfR8Q1wPFdvcosMxdm5mQao7sdgDe2Oq2faxe17nAwJEnSyFBNmhwN/Ay4B7g4M++KiC9HxD51xS1S0ZuZz1cjuB2BtSJiTPUN950Ga+nYjd9Vc4av+s9nbiwWC+CFP40vGm+9wkXVjLGoWpK6Xpd1u8/MK4Er+xz7Qj/n7jocMWubIYqI9SNirerrVYD30Bjp/RLYrzptKnB5XTlIkiS1o84Zoo2A86o6olE0prx+HBF3AxdGxFeA39FPt3tJkqRS6mzd8XvgzS2OP0yjnkiSJHWD7iqq7gh3qpYkSSNe2W2SJUlS93GGqCOtOy4ApgDzgRuBj2XmgEufvvjptetKcwlXfmX9YrEA/jRnXNF4m8+dWzTeit66Y1T4fyKStCKo85FZb+uO7YDJwJ4RsSNwAfAG4E3AKsDhNeYgSZIGkZnFXt2qzqLqBJZo3VHtLQBARNxIYy8iSZKkjqm1qDoiRkfEbcAs4OrMvKHps5WAg4Cf9nPtkRFxc0TcfM6vy3W7lyRpxOnJcq8uVbR1R0Rs0/TxfwDXZub/9nPtotYdh+60dZ1pSpKkEa506449gTsj4mRgfeBj7Vy/0gHH15jd4iZ/vVwsgKfnjS0aj/kLBj9nOLmxgyR1vy6euSmldOuOeyPicOB9wAGZ2V3NUyRJ0ojUidYdC4A/Ar+NCIBLM/PLNeYhSZIGkM4QdaR1h5tBSpKkruLgRJKkkc4ZIkteJUmSirfuaPr834FDMnO1we41//yv1ZXmEnZeOL5YLICnC8/R5dx5ZQOu4K07JGmF4BKnWh+Z9bbueLHahPG6iLgqM6+PiCnAWjXGliRJalttj8yyYYnWHdWqs9OAE+qKLUmSNBSdaN1xNHBFZs4c5NpXW3f89t4605QkaUTLniz26la1VrBk5kJgcrVB42UR8S7gg8CubVw7DZgGMOf0I7r3JyhJkpZ7pVt3vBt4PfBgtSnj+Ih4MDNfP9D1n/u32fUnWfnY+D8XiwVw8dy1i8Zj/vyi4cKiaknqfl08c1NK6dYdt2TmazJzUmZOAuYMNhiSJEmqW/HWHTXGkyRJS8Nl9+Vbd/Q5Z9A9iCRJkupm6w5Jkka4bl79VcpyMSD6xhP/WyzWl4/crlgsgGd+vKBovHylbFE1Y+wOI0nqfnUWVY+LiBsj4vaIuCsivlQdj4j4p4i4PyLuiYi/qysHSZLUhp6Cry5VvHUH8EZgIvCGzOyJiA1qzEGSJGlQdRZVJ7BE6w7gE8BHMrOnOm9WXTlIkqTBWUPUmdYdmwMfqtpyXBURW/Rz7aLWHT09L9WZpiRJGuFqHRBl5sLMnAxMAHaIiG2AlYFXMnMK8F/AOf1cOy0zp2TmlFGjVq0zTUmSRjZriIq37tgTmAH8oProMuDbg12/y4bb1JdcH2N22r5YLIBnf3RH0Xg5t3DrjrB1hySp+5Vu3XEv8ENgt+q0XYD768pBkiQNLnvKvbpV8dYdEXEdcEFEHEuj6PrwGnOQJEkaVPHWHZn5PPCXdcWVJEkaquVip2pJklSjLn6UVUptA6KIGAdcS2NV2Rjg+5l5ckTsDpxG4zHai8DBmfngQPf6/jvm1ZXmEmLrtxWLBfBs3lQ0HvMK/60fZVG1JKn7dWKn6rOAfTPznog4Cvg8cHCNeUiSpAF0c7FzKZ3YqTqBNarjawJP1JWDJElSOzqxU/XhwJURMQM4CDiln2sX7VR97kOOmSRJqo0bM3Zkp+pjgQ9k5gQamzKe3s+1i3aqPnjzjetMU5IkjXCld6p+P7BdNVMEcBHw0xI5SJKk1qwhqneV2frA/Gow1LtT9T8Da0bElpl5P7AHcM9g9xp/xjfqSnMJEbVOmi3hhYWvFI3XM7fs9zdq1bFF40mStDQ6sVP1EcAPIqIHeA44tMYcJEnSIJwh6sxO1ZfRaOoqSZLUFdypWpKkEc4ZoppXmUmSJC0Pap8hqmqIbgYez8y9ImJT4EJgHeBW4KDMHLA3x8K7/7fuNBcZM/m9xWIBvFi4qDpfWbloPFYvPObuWVg0XNiZRNKKIP0/sxK/rT7J4ivJ/hk4IzO3oFFUfViBHCRJkvpV907VE4C/BKZX7wPYDfh+dcp5wF/VmYMkSRpY9pR7dau6Z4j+FTiBVzfrXhd4PjMXVO9nAJu0urC5dcfZPyn3yEySJI08tQ2IImIvYFZm3tJ8uMWp2er65tYdh/3lzrXkKEmSBPUWVe8E7BMRHwDG0ehw/6/AWhExppolmoDd7iVJ6qjssai6zo0ZTwJOAoiIXYHjM/OjEXEJsB+NlWZTgcsHu9ePDyr3yGyf6yYXiwXw4oLCrTteWalovDFj3NlBktT9OvHb6rPAcRHxII2aorM7kIMkSapYVF2u2/01wDXV1w8DO5SIK0mS1A5bd0iSNMKlGzPaukOSJKkTrTsuAKYA84EbgY9l5vyB7nHk7BvqTnORvR7ZpVgsgDnFi6pXLxqPUf6rQ5K0qQMzAAAgAElEQVS6XTfX9pTSidYdFwBvAN4ErAIcXiAHSZKkfhVt3QGQmVdmhcYM0YQ6c5AkSQPLnij26lalW3csEhErAQcBP211YXPrjrnz/1xvlpIkaUQr3bqj2X8A12Zmy10Xm1t3rLzSGnWlKUnSiJdZ7tWtBi2qjoiVgb8FJjWfn5lfHuTSJVp3RMR3M/PAiDgZWB/4WDtJrrXyqu2cNizy1uuLxQJ4ZcG8ovEWlq3hhnAho7rTdredzu2Tj+t0GpK6RDurzC4HXgBuAea2e+N+WnccGBGHA+8Dds+0rl1SZzgYkl7VzbU9pbQzIJqQmXsOY8xvAX8EfhsRAJe2MdskSZJUm3YGRL+JiDdl5h1LG6RP6w53x5YkqYs4QzTAgCgi7gCyOueQiHiYxiOzADIzty2ToiRJUr0Gmq3Zq1gWkiRJHdTvgCgz/wgQEd/JzIOaP4uI79DYQ2hQfVt3NB3/d+CQzFxtsHtcuuqkdkINi5d+/lCxWADzehYUjbdwbuFVX7bukKSu183L4Utp57fjXzS/qQY4bx1CjL6tO4iIKcBaQ7iHJElSbfodEEXESRExG9g2Iv5cvWYDs2gsxR9Uq9Yd1YDqNBo7WEuSpA6zdccAA6LM/Fpmrg6clplrVK/VM3Pdao+hdrRq3XE0cEVmzhzowubWHT948ZE2w0mSJA1dO0vgL4mIt/Q59gLwx8zstwCmuXVHtTEjEbEx8EFg18GCZuY0YBrA7167r083JUmqSWb3ztyU0s6A6D+AtwC/p7Hk/k3A7cC6EfHxzPx5P9ct0boDuIvG0v0Hq00Zx0fEg5n5+oESeOMVR7TzvQyLa9/33WKxAOYvLFvEvWCeRdWSJPXVzm/HR4A3V41W3wpMBu4E3gOc2t9FmXlSZk7IzEnAh4H/ycy1M/M1mTmpOj5nsMGQJEmqV/aUe3WrdgZEb8jMu3rfZObdNAZID9eXliRJUjntPDK7LyLOAi6s3n8IuD8iVgbmtxOkuXVHn+OD7kEkSZLq1WMNUVszRAcDDwKfAo4FHq6OzQfeXVdikiRJpQw6Q5SZLwP/Ur36enHYM5IkSUW5yqyNAVFE7AR8EXhd8/mZuVk7Afq27ojG8rKv0Fh+vxA4KzP/bcB7jC+3qfUvVin7l6LnubI7CiyYO7povBhVeFWbJElLoZ0aorNpPCq7hcYAZqh6W3esUb0/GJhIo1i7JyI2WIp7SpKkYdLNO0iX0s4/31/IzKsyc1Zm/qn31c7NW7XuAD4BfDmzsfguM2cNOWtJkqRh1M6A6JcRcVpEvD0i3tL7avP+rVp3bA58qGrLcVVEbNHqwubWHdMvuqLNcJIkaagyy726VTuPzN5W/Tml6VgCuw10UavWHZWVgVcyc0pE/A1wDrBz3+ubW3fMvf+6Lv4RSpKk5V07q8yWdmn9Eq07IuK7wAzgB9U5lwHfHuxGT3zwS0uZwtDd2G93thXD/Plli6pX9NYdEY7VJWlFMOgjs4jYMCLOjoirqvdbR8Rhg13XT+uOA4Ef8urs0i7A/UudvSRJWmbZE8Ve3aqdGqJzgZ8BG1fv76exSePSOgX424i4A/gacPgy3EuSJGmZtVNDtF5mXhwRJwFk5oKIGNLy++bWHZn5PI2VZ5IkqQvYuqO9GaKXImJdGoXURMSOwAu1ZiVJklRQOzNExwFXAJtHxK+B9YH9as1KkiQVY+uO9laZ3RoRuwBbAQHcl5ltdbmHlq07dgdOozE79SJwcGY+ONA99n5ydrvhltlz88rF6oT58wqvMhtdOJ4kSUuh3wFRtUdQK1tGBJl5aZsx+rbuOAvYNzPviYijgM/TaOchSZI6oJs3TCxloBmivQf4LIFBB0RNrTv+icajt95rewdHawJPDJ6mJElSffodEGXmIcNw/97WHas3HTscuDIiXgb+DOzY6sKIOBI4EmCj1TdlnVXsAStJUh1cZdbeKrOl0ty6o89HxwIfyMwJNHapPr3V9Zk5LTOnZOYUB0OSJKlO7awyW1qtWnf8BHhDZt5QnXMR8NPBbvTQn2fWl2UfC3uGtMXSMhsVZUfl8xeUbt1R25hb0ghm25zh5SqzGmeIWrXuAPYF1oyILavT9qBRcC1JktQxg84QRcR44NPAazPziIjYAtgqM3881GDVLtdHAD+IiB7gOeDQod5HkiQNH1eZtTdD9G1gLvD26v0M4CtDCZKZ12TmXtXXl2XmmzJzu8zcNTMfHlLGkiRphRYRe0bEfRHxYESc2OLzlSPiourzGyJi0rLGbGdAtHlmngrMB8jMl2ls0ChJklYAPRnFXoOpNnT+JvB+YGvggIjYus9phwHPZebrgTOAf17Wn0E7A6J5EbEKr/Yy25zGjJEkSdJw2wF4MDMfzsx5wIU0apCb7QucV339fWD3iGVbpdTOKrOTaawEmxgRF9BYPXZwOzePiEeA2cBCYEFmTomIdWisLpsEPALsn5nPDXSf09bbuZ1ww+JTT/2yWCyAlUbXudBvSfOKrzJzMlGSul3JVWbN+wxWpmXmtKb3mwCPNb2fAbytz20WnVPVJ78ArAs8s7R5tdPL7OqIuJXGBooBfDIzhxLw3X3OPxH4RWaeUj0XPBH47FCSliRJy6dq8DNtgFNajc76ln23c86QDPrILCL+msbszk+qlWULIuKvliFm8zTXecCy3EuSJK1YZgATm95PYMk2X4vOiYgxNFqBPbssQdupITo5M1/ofZOZz9N4jNaOBH4eEbdUU2QAG2bmzOpeM4GW21BHxJERcXNE3PzrFx9oM5wkSRqqbiqqBm4CtoiITSNiLI29DK/oc84VwNTq6/2A/8lcts0D2ilgaTVoarfwZafMfCIiNgCujoh7202seUrtGxMPdIcESZJGgKom6GjgZ8Bo4JzMvCsivgzcnJlXAGcD34mIB2nMDH14WeO2M7C5OSJOp7EELoFjgL79yVrKzCeqP2dFxGU0KsefioiNMnNmRGwEzBrsPoed8YZ2wg2LLxxyw+AnDaOF2VM03ryewq00wtYdktTtum3WITOvBK7sc+wLTV+/AnxwOGO289vqGGAejZVhlwCvAP93sIsiYtWIWL33a+C9wJ0sPs01Fbh86GlLkiQNn3ZWmb1EYyXYUG0IXFZtCzAG+O/M/GlE3ARcHBGHAY8yzCM8SZI0NG3W9qzQ2ulltiVwPI19gxadn5m7DXRd1ZJjuxbH/wTsPtREJUmS6tJODdElwLeA6TQ2WJQkSSuQkhszdqt2BkQLMvOs2jMZwJh3fahYrEmr/bRYLIDH5yz1pppLZV66U7UkSX21MyD6UUQcBVxGUw+zzBx0A6R+WnecBuxNo1D7IeCQam8jSZLUAWXXO3endgZEvSvCPtN0LIHN2ozRt3XH1cBJ1T4D/wychK07JElSB7WzymzT4QyYmT9vens9jR0mJUlSh2TL1mAjSzu9zMZHxOcjYlr1fouI2KvN+7dq3dHsUOCqfuIuat0x/fwL2wwnSZI0dO08Mvs2jZ2p31G9n0Fj5dmP27h2idYdmXktQER8DlgAXNDqwubWHfNnPdBtm2hKkrTC6PG3bFsDos0z80MRcQBAZr4c1W6Lg+mndce1ETEV2AvYvZ1mbK989bh2wg2LySu/plgsgOfmzS4ab27hadEYZesOSVL3a2dANC8iVqFqdRIRm9O02qw/VbuOUZk5u6l1x5cjYk8aRdS7ZOacpU9dkiQNhx5riNoaEJ0M/BSYGBEXADsBB7dxXX+tOx4EVqbxCA3g+sz8+FLkLkmSNCzaWWV2dUTcCuwIBPDJPsvo+7uuv9Ydr1+aRCVJkurSTi+zd1Vf9ha7bB0R9BZHS5Kk5ZvL7tt7ZNa8IeM4GoXRtwADNneF1jtVN312PHAasP5gM06HXlauMHfvBeOKxQK4ccwqRePNi8JFzrbukCQtB9p5ZLZ38/uImAicOoQYfXeq7r3HHsCjQ7iPJEmqga072tiYsYUZwDbLGPcM4ASqlWuSJEmd1E4N0b/z6sBlFDAZuL3N+/fuVJ3Af2bmtIjYB3g8M28faDujamfrIwHess62bLbapDZDSpKkobCGqL0aopubvl4AfC8zf93m/ZfYqRr4HI09iQbUvFP1B1+3rzNJkiSpNu3UEJ23tDdvsVP1LsCmQO/s0ATg1ojYITOfXNo4kiRp6VlD1N4jsztoXesTQGbmtv1c13Kn6szcoOmcR4Apg60yu2zmzQN9PKz+eau/KBYL4D/+VHZV29wsPC1aelVbYaPCyUtJWhG088istxv9d6o/PwrMAQabOWq5U/XSJClJkurjDFF7A6KdMnOnpvcnRsSvM/PLA13U307Vfc6Z1EZ8SZKkWrXzPGPViHhn75uIeAewan0pSZKkkpIo9upW7cwQHQacExFr0qglegE4tNasJEmSCmpnldktwHYRsQYQmflCuzfvr3VHRBwDHE1jGf9PMvOEge5zwEZvazfkMttgz7JFsmteOLpovLk9hUfnpVt3pE/CJWmoSv9q6EbtrDLbEPgqsHFmvj8itgbenplntxljsdYdEfFuYF9g28ycW+1RJEmS1DHt1BCdC/wM2Lh6fz/wqWWI+QnglMycC409ipbhXpIkaRn1EMVe3aqdAdF6mXkx1aq8zFxA4xFYO3pbd9xSteIA2BLYOSJuiIhfRcT2rS6MiCMj4uaIuPmBF//QZjhJkqSha6eo+qWIWJdqc8aI2JFGYXU7WrXuGAOsDewIbA9cHBGbZeZixTvNrTsOet3fuPudJEmqTTsDouOAK4DNI+LXwPrAfu3cvEXrjh2AGcCl1QDoxojoAdYDnl6K/CVJ0jJy1qG9VWa3RsQuwFY02nXcl5nzB7uuv9YdwIvAbsA1EbElMBYYsHXHWR8p98xx9PZTisUCWOviG4vGm1v6b/3osqvoJElaGu2sMvsg8NPMvCsiPg+8JSK+kpm3DnJpy9YdETGWxr5GdwLzgKl9H5dJkqRy3LCkvUdm/5CZl1S7Vb8P+DpwFjDg5kD9te7IzHnAgUuRqyRJUi3aWWXWu6LsL4GzMvNyGo+5JEnSCqAnotirW7UzIHo8Iv4T2B+4MiJWbvM6SZKk5UI7j8z2B/YEvp6Zz0fERsBn2rl5q9YdETEZ+BYwjkbrjqMyc8DK4pU/fVo74YZFz5MPFYsFsE7cVjTe3NKD81GOnSWp21nI294qsznApU3vZwIzhxBjsdYdwKnAlzLzqoj4QPV+1yHcT5IkaVi1M0M03BJYo/p6TeCJDuQgSZIqrjKrvxaoVeuOTwGnRcRjNFasndTqwubWHdPP/17NaUqSpJGs7hmiVq079gOOzcwfRMT+wNnAe/pe2Ny6Y/4zD/t4U5KkmvR07+KvYmodEPXTumMq8MnqlEuA6YPdZ8HPvl1bjn2NeU/ZLZLWLfzU0qJqqWG7207n9snHdToNSV2itt9WEbFqRKze+zWN1h130qgZ2qU6bTfggbpykKT+OBiSXtVDFHt1qzqnJ/pr3fEicGZEjAFeAY4c4B6SJEm1q21ANEDrjuuAt9YVV5IkDY2Fuu44LUmS5IBIkiSp1iVOEbEWjVVk29CYkTsUuA+4CJgEPALsn5nPDXSff//7P9SZ5mKOfd9KxWIBrN9Tdkw6p/gqs+4toJMkNbjsvv4ZojOBn2bmG2jUE90DnAj8IjO3AH5RvZckSeqYOpfdrwG8i8bGi2TmvMx8HtgXOK867Tzgr+rKQZIkDa6n4Ktb1TlDtBnwNPDtiPhdREyv9iPasGoQ29sodoNWFze37rjhRbcqkiRJ9alzQDQGeAtwVma+GXiJITwey8xpmTklM6e8bbUt6spRkqQRLwu+ulWdRdUzgBmZeUP1/vs0BkRPRcRGmTkzIjYCZg12oy88dW2NaS7uk88+USwWwHoLiobjoZUK/3UMFzJKkrpfbb+tMvNJ4LGI2Ko6tDtwN3AFjX5mVH9eXlcOkiRpcD1R7tWt6u4segxwQUSMBR4GDqExCLs4Ig4DHgU+WHMOkiRJA6q72/1twJQWH+1eZ1xJktS+bl79VYoFHpIkacSr+5GZJEnqcs4QdaZ1x98AewPzgIeAQ6oNG/u19dqvrTPNxfT84bZisQA2WDi/aLy7x44uGo9RTkJKkrpfJ1p3XA1sk5nbAvcDJ9WcgyRJGkBGuVe3Kt66IzN/npm9u+9cD0yoKwdJkqR2dKJ1R7NDgataXdzcuuOZOU/WmKYkSSObvcw62LojIj4HLAAuaHVxc+uO9ca/psY0JUnSSNeJ1h1ExFRgL2D3zBy0l8SPJo2tLcm+em66vlgsgPVWfqVovLmMLxovRnXxA+NhEKO6uTOPJKldtQ2IMvPJiHgsIrbKzPuoWndExJ7AZ4FdMnNOXfElSVJ7uvlRVimdaN1xE7AycHVEAFyfmR+vOQ9JkqR+daJ1x+vrjClJkobGh/+27pAkSbJ1hyRJI13Pir3+pS3FW3dk5m+rz44HTgPWz8xnBrrPet/9ap1pLubZqWU3zl5zzZWKxps3e1zReISTkJKk7lf3DFFv6479qsLq8QARMRHYA3i05viSJGkQrjLrQOuO6uMzgBOwjkuSJHWB4q07ImIf4PHMvH2gi5tbd0y/8Ic1pilJ0shm6456H5n1tu44JjNviIgzgS/SmDV672AXZ+Y0YBrA3IeudyZJkiTVpnTrji8CmwK3V5syTgBujYgdMrPfDq757OM1prm4Gx7cqFgsgHf8RbnvDWD+7MJjy1EWVUtSt3PWocZHZtUA57GI2Ko6tDtwa2ZukJmTMnMSjUHTWwYaDEmSJNWtE607JElSF3Efos607mj+fFKd8SVJktrhTtWSJI1w3bz6q5TlYkB06z7/XSzWBgEXrVxu9+hdXzO6WCyAuQ8V/mtvUbW61Ha3nc7tk48rFu/2ycex3W2nF4snaWhq/W0VEWtFxPcj4t6IuCci3l4dPyYi7ouIuyLi1DpzGKqSgyFJnVNyMAQ4GJK6XPHWHRHxbmBfYNvMnBsRG9ScgyRJGoDL7mscEDW17jgYGq07gHkR8QnglMycWx2fVVcOkiRJ7SjeugPYEtg5Im6IiF9FxPatLm5u3XH5nD/UmKYkSSNbD1ns1a3qHBD1tu44KzPfDLwEnFgdXxvYEfgMcHFU21Y3y8xpmTklM6fsO37TGtOUJEkjXenWHSdWxy/NzARujIgeYD0as0kt7T/3vhrTXNzrRpUtaRqz4WpF483PwqvMlhzrSpK6jMvuy7fuuBv4IbAbQERsCYwFnqkrD0mSpMF0onXHS8A5EXEnMA+YWs0WSZKkDvCXcOdadxxYZ1xJkqShWC52qpYkSfWxhmg5GRDNXTi/WKwHX3yiWCyAWP9tRePN44Wi8WzdIUlaHtQ6IIqItYDpwDY0HlEeCrwMfAsYBywAjsrMG+vMQ5Ik9a/HBcHlW3cAFwNfysyrIuIDwKnArjXnIUmS1K9OtO5IYI3qtDWBss+oJEnSYrp5B+lS6pwham7dsR1wC/BJ4FPAzyLi6zT2QXpHq4sj4kjgSIDVxm3AuLFr1ZiqJEkayTrRuuMTwLGZORE4Fji71cXNrTscDEmSVJ8s+OpWnWjd8U4aM0UAl9Aouh7QuePeUkuCrfzVc9cWiwUQ665TNN58nisajyi8yqzHxaOSpKHrROuOJ4BdqmO7AQ/UlYMkSVI7OtG643LgzIgYA7xCVSckSZI6w7n1zrTuuA54a51xJUnSiiki1gEuAiYBjwD7Z2bLepBqxfs9wGWZefRA93UbYUmSRrgesthrGJwI/CIztwB+Ub3vzz8Cv2rnpnXuQ7QVjRFcr82ALwDn0+bIrtdul7yvniRbeU/houq11i4ab34Wnhi1dYckaXjty6sbOp8HXAN8tu9JEfFWYEPgp7RuNL+YOouq78vMyZk5mcYjsjnAZQxtZCdJkmpWctl9RBwZETc3vYZaS7xhZs4EqP7coO8JETEK+BfgM+3etFRz192BhzLzjxHR1shOkiSteDJzGjBtoHMi4v8Br2nx0efaDHMUcGVmPhbRXqO2UgOiDwPfq75ebGQXEUuM7GDxnar//dNTOWyfXUvkKUnSiNNtq8wy8z39fRYRT0XERtUYYiNgVovT3g7sHBFHAasBYyPixczs96lU7QOiasn9PsBJQ7mueQT58rXndvPmlpIkqZwrgKnAKdWfl/c9ITM/2vt1RBwMTBloMARlVpm9H7g1M5+q3j9VjegYYGQnSZIKWc5WmZ0C7BERDwB7VO+JiCkRMWj3i/6UeGR2AK8+LoM2RnZ9jd70zfVk1sJaq6xWLBYAa5Zt3bEgFxaNt6KvMmvz0bQkaZhk5p9o1Cb3PX4zcHiL4+cC5w5231p/W0XEeBqjt0ubDrcc2UmSpM6wuWv9O1XPAdbtc6zlyE6SJKlTSq0ykyRJXarbVpl1wopd4CFJktSGTrTu2ATYG5gHPAQckpnPD3Sv2Uf9XV1pLmHTVVvtA1WfWK1s6455pYuqrTqWpK6XXV3dU0YnWndcDWyTmdsC9zPE/YkkSZKGW6lHZotad2TmzzNzQXX8emBCoRwkSZJaKjUgam7d0exQ4KpWFzQ3fzvvjzNrTU6SpJGsp+CrW9U+IGpq3XFJn+OfAxYAF7S6LjOnZeaUzJwy9XUb1Z2mJEkawUosu+/buoOImArsBeyemVZySZLUQcPUUmO5Vrx1R0TsCXwW2KXauHFQf31rue2Spoxdd/CThtOqaxYNN9/WHZIkLaHWkUZT646PNR3+BrAycHU0lmRfn5kfrzMPSZLUP+eHOtO64/V1xpQkSRoqW3dIkjTCWUNk6w5JkqTyrTsy81+rz48HTgPWz8xnBrrXb5++t640l3DMursWiwUQ49cqGm9+6V0gLKqWpK7XzfsDlVLbgCgz7wMmA0TEaOBxGq07iIiJNIqtH60rviRJUruKt+6o3p8BnICF7ZIkdVwW/E+3Kt66IyL2AR7PzNsHuqC5dUdPz0slcpQkSSNU7avMmlp3nFTtS/Q54L2DXZeZ04BpACuN3aR7h5SSJC3nrCEq3LojIt4EbArcXm3KOAG4NSJ2yMwn+7vB8RvvUiDNhh3X7zeNWsTK44vGW5iF/9qHRdWSpO5XtHVHZt4BbND7QUQ8AkwZbJWZJEmqTzfX9pRS6z/fm1p3XFpnHEmSpGVRvHVHn88n1RlfkiSpHbbukCRphLOo2tYdkiRJnWndERHHAEcDC4CfZOYJA93rHz7b71O3YZczC4+TV1q5aLgFubBoPFt3SFL360mLqou37oiIdwP7Attm5tyI2GCA20iSJNWuVA3RotYdEXEacEpmzgXIzFmFcpAkSS04P9SB1h3AlsDOEXFDRPwqIrZvdUFz645zrruzUJqSJGkkKtq6oynm2sCOwPbAxRGxWebiDzCbW3fMOesYB6+SJNWkxzmisq07qvczgEurAdCNEdEDrAc83d8NVvrgsfVnWVlw/Q+LxQKIMWOLxiteVG3rDknScqDEb6tFrTsqPwR2A4iILYGxgK07JEnqkCz4n27VidYd5wCbRcSdwIXA1L6PyyRJkkoq3rojM+cBB9YZV5Iktc+dqt2pWpIkyV5mkiSNdK4y60DrDuAa4FvAOBqtO47KzBsHutf8b3+lpiyXNHrvqcViATBqdNFwC7PwxKitOyRJy4HirTuA/wK+lJlXRcQHgFOBXevKQ5IkDaybV3+VUuqf74tad9DYIXyN6viawBOFcpAkSWqpE607PgWcFhGPAV/n1R2sF7NY647r7yuUpiRJGolqHxA1te64pDr0CeDYzJwIHAuc3eq6zJyWmVMyc8qhO25Vd5qSJI1YPQVf3aoTrTumAp+svr4EmD7YDU785ks1pbakf5m6cbFYnTC/p3DrjhVcjFqxn7uPihX7+5OkXiUGRH1bdzwB7EJjtdluwAMFcpAkSf2wYUTNA6Km1h0fazp8BHBmRIwBXgGOrDMHSZKkwXSidcd1wFvrjCtJktrnxoy27pD+f3v3Hm1lVa9x/PsAXhBNRQUvUKhhWghkW45pogfMzEylo6Vphyw1z8hEOo3UYeeYXTVNs2NZiqajzDIvSZqEx+MlK1REEBQVKjOUQE00EgHZv/PH+y5cbBb7onvOtfZez4exxl63933m2uy91tzzne/8mZmZuXSHmZlZs2vks79yST2HaDJwIsVijHOBE4AdgJ8BA4FZwCciYlV7+/n+s/elbOY6vp0tqZT5rK/spTuUdxAycr8+MzPrFZJ9WknaCTgNaImIEUBfigUazwcujojhwIvAp1O1wczMzDoWGf81qtR/vvcD+pdnlG0GLKY41f6G8vFrgCMTt8HMzMysXSmLuz4j6ULgaWAFMB14CFgWEa+VT1sE7FRre0knU56Sr75b0qfPgFRNNTMza2o+yyztIbOtgSOAnYEdgQEUq1a3VfN/obp0hztDZmZmllLKSdUHAX+OiOcAJN0E7AtsJalfOUo0hE5Uux8/eGTCZq6r9YVF2bIA+my1fda819YOzmXSxys7mJk1Oq9UnXYO0dPAPpI2kyRgPPAYcBdwVPmcicAtCdtgZmZm1qFkHaKIuJ9i8vQsilPu+wCXA2cAn5e0kGIV65rV7s3MzCwPV7tPX7rjHOCcNnf/CRiTMtfMzMysK7xStZmZWZNr5PWBcukRHaLrD2x3Ietu1brgoWxZABo1Lmte9pWqPanaGtSo2RcxZ/Tn690MM2sQST+tJE2W9KikeZKuk7SppGslPVHed5WkjVK2wcysFneGzKxaPUp3XAvsDuwJ9KeodWZmZmZ10kpkuzSq1IfMKqU7VlOU7ng2IqZXHpT0AMVaRGZmZmZ1k/K0+2eASumOxcBLbTpDGwGfAKbV2l7SyZJmSpp59YJnUjXTzMys6UVEtkujylq6Q9LxVU/5PnBvRPy21vbVpTs+ObxmuTMzMzOzblGP0h0/kXQOsB3wmc7sqP/5303WyLZWf+/L2Zx0u5EAABRISURBVLIA+uy+T9a8Na2ZzzKTzzIzM2t0jTy3J5eUHaK1pTsoqt2PB2ZKOhH4ADA+Ivc54GZmZmbrS9Yhioj7JVVKd7wGPExRuuOfwF+APxQlzrgpIr6Sqh1mZmbWPi/MWJ/SHT1iMUgzMzNrHu6cmJmZNbnWBj77K5ce0SFaM/eubFnP3/5itiyAwR99OWteq0t3mJmZrSd76Y6qx/5H0vKU+WZmZtaxyHhpVPUo3YGkFmCrVNlmZmZmXZG9dIekvsAFwMeBCYnzzczMrANeh6g+pTtOBaZGxOL2tq8u3XHlr3+XqplmZmZm6UaI2pTuWAb8QtK/A0cDB3a0fURcTrFuESt+c6m7rmZmZol4hCh/6Y5zgf7AwnJRxs0kLYyIt7e3o1+e8IeEzWxrcMYsmPDKS1nz1uQ+y8ylO8zMrAdI+Wm1tnSHit7PeOCiiNg+IoZFxDDglY46Q2ZmZmap1aN0h5mZmTWQ8MKMdSndUf345inzzczMzDqjR6xUbWZmZul4UnXiDpGkycCJFItTzgVOAFYCX6M422wNcFlEfLe9/Zzy8oyUzVzHMdvulS0L4Mh/5C0Vkr1ejUt3mJlZD5DytPvKStXvjIgVkq6nWKlawFBg94holTQoVRvMzMysY+ERovwrVVOMDn08ojj/OyKWJm6DmZmZWbvqsVL1rsDHylWob5c0vNb21StVr1qdtyK8mZlZM4mIbJdGlbK4a/VK1TsCAyQdD2wCvBoRLcAVwFW1to+IyyOiJSJaNt7oLamaaWZmZpZ9pep9gUXAjeVzbgZ+lLANZmZm1gGfZZa2Q7R2pWpgBcVK1TOBl4FxFCNDBwBPdrSjbTbNN0I0a9WSbFkALHs+a1z20h29nOQ3ETOz3qAeK1X3B64tT8lfTnFavpmZmdVJI8/tyaUeK1WvBD6UMtfMzMysK7xStZmZWZPzHKK01e7NzMzMeoR6lO7YD7iAojO2HPhkRCxsbz+/3HxIymauY9zfn8iWBRDL8pbuyH6cWO5zm5k1Oq9UnXYdokrpjpaIGAH0pSjdcRlwXESMBn4KfClVG8zMzMw6I/Wf75XSHf14vXRHAJXz6Lcs7zMzMzOrm5Sn3T8jqVK6YwUwPSKmSzoR+LWkFRRrEu1Ta3tJJwMnA/zXwD05aou3pWqqmZlZU2v1afd1Kd0xGTg0IoZQrFJ9Ua3tq0t3uDNkZmZmKeUu3bEfMCoi7i+f83NgWsI2mJmZWQc8qbo+pTuOlrRbRDwJvB+Y39GO3jH11ITNXNdLLZ/KlgXAi8uyxmUv3dEn81lmrS5NYmZmXVeP0h2LgBsltQIvApl7IGZmZlbNc4jqU7rj5vJiZmZm1iWSBlJMuRkGPAV8NCLWW9RP0rcoSoX1Ae4AJkU7i/F51TwzM7MmFxn/dYMzgTsjYjhwZ3l7HZL2pZi3PBIYAewNHNDeTt0hMjMzs57kCOCa8vo1wJE1nhPApsDGwCbARsCS9naaunTHJOAkQMAVEfGdzg51rWPjTVM2cx2SsmUBtD7397x5mY8TS32z5pmZWdfl/GyoXmewdHlEXN6FXQyOiMUAEbFY0qC2T4iIP0i6C1hM0Qe5NCLaPYkrWYdI0giKztAYYBUwTdJt5X13RsR5ks6kGOo6I1U7zMzMrHGUnZ92O0CS/hfYvsZDZ3cmQ9LbgT2ASjHUOySNjYh7N7RNyhGiPYAZEfFK2bh7gAkUQ10Hls+5Brgbd4jMzMzqptHWIYqIgzb0mKQlknYoR4d2AJbWeNoEij7I8nKb2ykqY2ywQ5RyDtE8YKykbcq1iA4FhtJmqAtYb6gLiiE1STMlzZxy/a8SNtPMzMx6kKnAxPL6ROCWGs95GjhAUj9JG1FMqK7PIbOImC/pfIpT3ZYDcyjWI+rs9muH1FY+fk9jdV3NzMx6kR62DtF5wPWSPk3R8TkaQFILcEpEnAjcAIwD5lJMsJ4WEe2OrqReh+hK4Mqyod+gWJSxM0Nd61h01DdSNnMdA/tvkS0LYM2S5Vnz2lmCIY3cK1WbmVmvFhEvUFS/aHv/TODE8voa4DNd2W/ST6vKzG9JbwU+AlxH54a6zMzMLJMetg5REklHiChKdGwDrAY+GxEvSqo51GVmZmZWL6kPme1f476aQ11mZmZm9ZJ6hMjMzMwaXERrvZtQd57xamZmZk2vHqU7LgA+TLF69R+BEyJiWXv7Ofy5dh/uVsMH7JgtC2DV3zq9EkG3aOQJbWZmVh+t/mxIN0LUpnTHKOAwScMp1iUaEREjgSeBs1K1wczMzKwzUh4yW1u6IyJeA+4BJkTE9PI2wAxerzNiZmZmdRAR2S6Nqh6lO6p9Cri91sbVpTteXNHh2o1mZmZmb1jdSndIOru8fe0Gtl9buuNdg/+lcbuUZmZmPZznENWndAeSJgKHAeOjE+NnT/1jScpmruPgQTtnywJYvvSFrHku3WFmZra+1GeZDYqIpVWlO94r6RDgDOCAiHglZb6ZmZl1rJHn9uRSj9IdlwKbAHdIgmLi9SmJ22FmZma2QfUo3fH2lJlmZmbWNa0eIfJK1WZmZmauZWZmZtbkXMWgDqU7qh77AnABsF1EPN/efr69zftSNnMdO726JlsWwEvRP2te9olz6t2DkH3kNxEzs94gWYeoTemOVcA0SbdFxAJJQ4H3A0+nyjczM7PO8VlmdSjdUT52MfBF8BidmZmZ1V/20h2SDgeeiYg57W1cXbrjt8sXJGymmZmZNbt6lO44Gzi4E9uvLd3xg6HHeyTJzMwsEZfuyF+6YwlwHDCnXJRxCDBL0piI+NuG9jPxuyNSNnMdL108LVsWwKNPDM6al51Ld5iZWQ+QvXRHRFxS9fhTQEtHZ5mZmZlZOp5UXYfSHYnzzMzMzLose+mONo8PS5lvZmZmHXPpDpfuMDMzM3PpDjMzs2bnOUR1Kt0h6XPAqRSn4d8WEV9st5H7Tmjv4W61xWOPZcsCWLowb6kQ/8ibmZmtL3vpDopT7Y8ARkbESkmDUrXBzMzMOuZ1iNKOEK0t3QEgqVK6owU4LyJWAkTE0oRtMDMzM+tQ9tIdwG7A/pLul3SPpL1rbVxdumPKj3+esJlmZmbNLSKyXRpVPUp39AO2BvYB9gaul7RLtPkuVZfuWL3kicb9DpqZmVmPl7t0xyKKQ2k3lR2gByS1AtsCz21oP69+dXLKZq6j3+GHZcsCeL7v77PmZSev7GBm1ui8DlEdSncArcA44G5JuwEbAy7dYWZmZnWTvXSHpKuAqyTNozj7bGLbw2VmZmaWT/gss/ylOyJiFXB8ylwzMzOzrvAEDzMzM2t6PaJ0x8Rf5WvmdZNGZ8sCeK7v77LmZdenb968aM2bZz3WqNkXMWf05+vdDLOG4EnViUeIJE2SNE/So5JOL+8bLWmGpNnlOkNjUrbBzKwWd4bMrFo9Snd8Czg3Im6XdGh5+8BU7TAzM7P2+dym+pTuCOAt5XO2BJ5N2AYzMzOzDqXsEM0Dvl6edr+ConTHTOB04DeSLqQ4ZLdvrY0lnQycDDB64Eh23vxtCZtqZmbWvHzafcI5RBExH6iU7pjG66U7/gOYHBFDgcmUK1nX2P7yiGiJiBZ3hszMzCylepTu+CYwqXzKL4ApHe1n6uKHUjVxPX223j5bFsDzrM6al51Ld5iZNTzPIUp/ltmg8muldMd1FHOGDiifMg5YkLINZmZmZh2pR+mOk4BLJPUDXqWcJ2RmZmb14RGi+pTuuA94T8pcMzMzs67oEStVm5mZWToeH3ItMzMzM7PiuGFvvQAnO895jZblPOc5r3nycr82X974pbePEOWesO28npvXm1+b85znvPrl+cShHqK3d4jMzMzMOuQOkZmZmTW93t4hutx5zmvALOc5z3nNk5f7tdkbpHLSl5mZmVnT6u0jRGZmZmYdcofIzMzMml6v7BBJOkTSE5IWSjozQ95VkpZKmpcha6ikuyTNl/SopEmJ8zaV9ICkOWXeuSnzqnL7SnpY0q0Zsp6SNFfSbEkzM+RtJekGSY+X/4/vTZj1jvJ1VS4vSzo9VV6ZObn8WZkn6TpJmybMmlTmPJrqddX6/ZY0UNIdkhaUX7dOnHd0+RpbJbUkzrqg/Nl8RNLNkrZKnPfVMmu2pOmSdkyZV/XYFySFpG1T5kn6sqRnqn4HD+2uPOteva5DJKkv8D3gg8A7gWMlvTNx7NXAIYkzKl4D/jMi9gD2AT6b+PWtBMZFxChgNHCIpH0S5lVMAuZnyKn414gYHRHd9mHTjkuAaRGxOzCKhK8zIp4oX9doihqCrwA3p8qTtBNwGtASESOAvsAxibJGACcBYyi+j4dJGp4g6mrW//0+E7gzIoYDd5a3U+bNAz4C3NuNORvKugMYEREjgSeBsxLnXRARI8uf0VuB/06ch6ShwPuBp7sxa4N5wMWV38OI+HU3Z1o36XUdIoo3x4UR8aeIWAX8DDgiZWBE3Av8PWVGVdbiiJhVXv8HxYfpTgnzIiKWlzc3Ki9JZ+JLGgJ8CJiSMqceJL0FGAtcCRARqyJiWab48cAfI+IviXP6Af0l9QM2A55NlLMHMCMiXomI14B7gAndHbKB3+8jgGvK69cAR6bMi4j5EfFEd2V0kDW9/H4CzACGJM57uermALrx/aWd9+aLgS92Z1YHedYD9MYO0U7AX6tuLyJhh6GeJA0D3g3cnzinr6TZwFLgjohImgd8h+LNqjVxTkUA0yU9JCn1qrK7AM8BPyoPCU6RNCBxZsUxwHUpAyLiGeBCir+8FwMvRcT0RHHzgLGStpG0GXAoMDRRVluDI2IxFH+kAIMy5eb2KeD21CGSvi7pr8BxdO8IUa2sw4FnImJOypw2Ti0PC17VnYdXrXv1xg6RatzX69YWkLQ5cCNwepu/sLpdRKwph7OHAGPKQxVJSDoMWBoRD6XKqGG/iNiL4jDrZyWNTZjVD9gLuCwi3g38k+493FKTpI2Bw4FfJM7ZmmL0ZGdgR2CApONTZEXEfOB8ikM804A5FIeUrRtIOpvi+3lt6qyIODsihpZZp6bKKTvOZ5O409XGZcCuFFMOFgPfzphtXdAbO0SLWPevxCGkG7KvC0kbUXSGro2Im3Lllod27ibtfKn9gMMlPUVxuHOcpJ8kzCMini2/LqWYXzMmYdwiYFHVKNsNFB2k1D4IzIqIJYlzDgL+HBHPRcRq4CZg31RhEXFlROwVEWMpDlUsSJXVxhJJOwCUX5dmys1C0kTgMOC4yLtY3U+Bf0u4/10pOutzyveYIcAsSdunCoyIJeUfla3AFaR9f7E3oTd2iB4Ehkvaufyr+Bhgap3b1G0kiWL+yfyIuChD3naVs0wk9af4wHs8VV5EnBURQyJiGMX/3f9FRJIRBgBJAyRtUbkOHExxKCaJiPgb8FdJ7yjvGg88liqvyrEkPlxWehrYR9Jm5c/qeBJOGpc0qPz6VopJxzleIxTvKRPL6xOBWzLlJifpEOAM4PCIeCVDXvVE+MNJ+/4yNyIGRcSw8j1mEbBX+XuZRKXjXJpAwvcXe5MqZe9704ViLsGTwB+BszPkXUcxFLqa4hfs0wmz3kdxCPARYHZ5OTRh3kjg4TJvHvDfGf8fDwRuTZyxC8WhljnAo5l+XkYDM8vv6S+BrRPnbQa8AGyZ6f/tXIoPtXnAj4FNEmb9lqJDOQcYnyhjvd9vYBuKs8sWlF8HJs6bUF5fCSwBfpMwayHFPMzK+8sPEr+2G8uflUeAXwE7pcxr8/hTwLaJX9+Pgbnl65sK7JDi59SXN39x6Q4zMzNrer3xkJmZmZlZl7hDZGZmZk3PHSIzMzNreu4QmZmZWdNzh8jMzMyanjtEZplIGlar6nb52FckHVTj/gMl3bqBbZ7qzkrdtfYr6ffdvf9OtmFKhqLMZmZr9at3A8wMIiJnKYFOi4hkq0x3kHtiPXLNrHl5hMgsr76SrpD0qKTp5erfSLpa0lHl9UMkPS7pPorVlynv36bc5mFJP6Sqbp+k4yU9IGm2pB9K6lvev7wsnDlH0gxJg9s2qIP9Li+/HijpHknXS3pS0nmSjisz50ratXzedpJulPRgedmvvP/LZWHLuyX9SdJp5f0DJN1Wtm+epI+V998tqaW8fmyZMU/S+dVt6+i1mZl1ljtEZnkNB74XEe8CltGmbpOkTSnqHX0Y2B+orrF0DnBfFEVhpwJvLbfZA/gYRZHa0cAaiqrhAAOAGRExCrgXOKlGm2rut4ZRwCRgT+ATwG4RMQaYAnyufM4lwMURsXf52qZUbb878AGKWk7nlDX5DgGejYhRETGCokhr9fdjR4oCruMoVvjeW9KRXXhtZmad4g6RWV5/jojZ5fWHgGFtHt+9fM6CKJaRry5sO7ZyOyJuA14s7x8PvAd4UNLs8vYu5WOrgMocpFp57e23rQcjYnFErKQoizO9vH9u1X4PAi4t2zEVeEulVhxwW0SsjIjnKYqhDi63PUjS+ZL2j4iX2mTuDdwdRbHYSuX1sV14bWZmneI5RGZ5ray6vgboX+M57dXTqfWYgGsi4qwaj62O1+vzrGHDv/OdqeFT3fbWqtutVfvtA7w3Ilas00Cp7fZrgH4R8aSk91DUH/ympOkR8ZXqTdtpT2dfm5lZhzxCZNZYHgd2rszJoahSX3Ev5aEwSR8Eti7vvxM4qqry+0BJb+tC5ob2+0ZMB06t3JA0ur0nl4fEXomInwAXAnu1ecr9wAGSti3nRR0L3PMm2mdmVpM7RGYNJCJeBU4GbisnVf+l6uFzgbGSZgEHA0+X2zwGfAmYLukR4A5ghy7E1tzvG3Qa0CLpEUmPAad08Pw9gQfKQ2xnA1+rfjAiFgNnAXdRVLSfFRG3vIn2mZnV5Gr3ZmZm1vQ8QmRmZmZNzx0iMzMza3ruEJmZmVnTc4fIzMzMmp47RGZmZtb03CEyMzOzpucOkZmZmTW9/wfaSBN5JS8YMAAAAABJRU5ErkJggg==%0A" alt="img">
3. self-Attention
self-attention是BERT的重要思想,其与位置编码结合,解决了文本数据的时序相关性的问题,从而一举结束了依靠RNN、LSTM、GRU等之前一直用来解决时序问题的网络模型。self-attention通俗的说就是信息向前传播时动态的计算权重的一种方式,与CNN常见的MaxPooling、MeanPooling不同的是,attention模型是经过训练,当不同信息传入时,自动的调整权重的一种结构。self-attention的具体结构如下图所示:
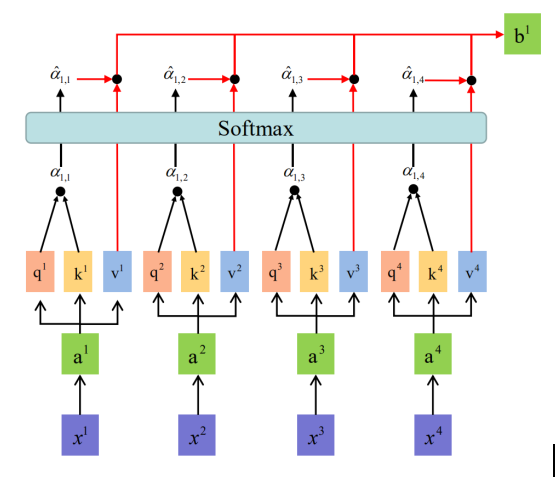
具体的,将上图的过程进行详细的解释,主要是拆分成4个步骤:
1)\(x^1, x^2, x^3, x^4\)代表的是经过embedding的4条时序文本信息,首先将4条信息加上位置向量,得到\(a^1, a^2,a^3, a^4\),这样做的目的上文已经说过,是为了获取文本的时序相关性。
2) 对每条信息分配三个权重\(W_Q, W_K, W_V (embed.dim*embed.dim)\),分别与\(a^1, a^2, a^3, a^4\)相乘后形成3个矩阵\(Q, K, V\)也就是上图的\(q^i, k^i, v^i\)。
K = Linear(a^1) = a^iW^K \\
V = Linear(a^1) = a^iW^V
\]
3) 将\(q_1\)分别与\(k^1, k^2, ...,k^i\)点乘,得到\(\alpha_{1, i}\),再有softmax的计算公式,计算得\(\hat\alpha_{1, i}\)。
\hat\alpha_{1, i} = exp(\alpha_{1, i})/\sum_j{exp(\alpha_{1, j})}
\]
4)最后按照softmax输出的权重对\(V\)进行加权,计算得\(b^1\)。使用同样的方法计算得\(b^2, b^3, ...,b^i\)。将\(b^1, b^2, b^3, ...,b^i\)进行合并,完成self-attention。
\]
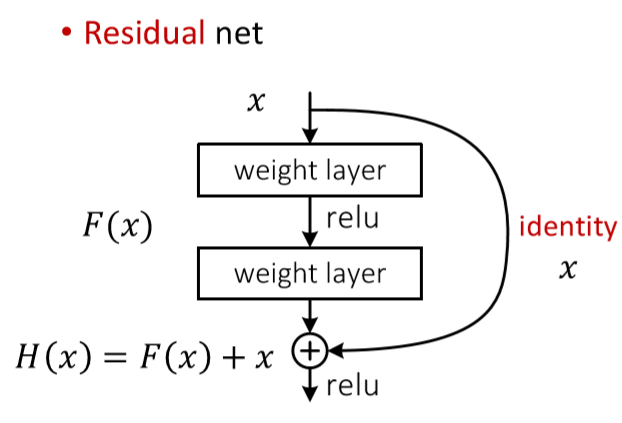
4. 残差连接
残差连接是训练深层模型时惯用的方法,主要是为了避免模型较深时,在进行反向传播时,梯度消失等问题。具体实现时,当网络进行前向传播时,不仅仅时按照网络层数进行逐层传播,还会由当前层隔一层或多层向前传播,如下图所示:
5. 模型实现
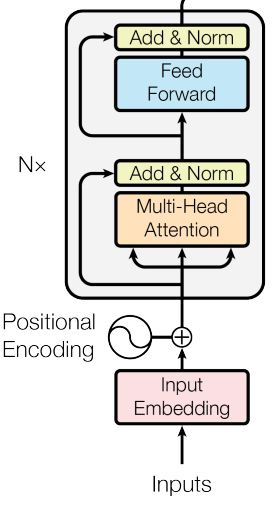
以上是BERT的整体结构,Input输入的是文本数据,经过Embedding加上位置向量Positional Encoding。Multi-Head Atention为多头的self-Attention,实际上就是将self-attention的Q、K、V均分成n份,分别进行计算。Add&Norm为残差计算和标准化;Feedward为全连接层,进行前向传播。其中\(N_x\)为基本单元的个数,是可以条调整的超参数。
6. Bert模型预训练策略
在预训练Bert模型时,论文提供了两种策略:
(1) Masked LM
在BERT中, Masked LM(Masked language Model)构建了语言模型, 这也是BERT的预训练中任务之一, 简单来说, 就是随机遮盖或替换一句话里面任意字或词, 然后让模型通过上下文的理解预测那一个被遮盖或替换的部分, 之后做的时候只计算被遮盖部分的
, 其实是一个很容易理解的任务, 实际操作方式如下:
- 随机把一句话中
替换成以下内容:
- 这些
有
;
- 有
的几率被替换成任意一个其他的
;
- 有
的几率原封不动.
- 这些
- 之后让模型预测和还原被遮盖掉或替换掉的部分, 模型最终输出的隐藏层的计算结果的维度是:
我们初始化一个映射层的权重:
我们用完成隐藏维度到字向量数量的映射, 只要求
和
的矩阵乘(点积):
的和为
, 我们就可以通过
里概率最大的字来得到模型的预测结果, 就可以和我们准备好的
做损失(
)并反传梯度了.
注意做损失的时候, 只计算在第1步里当句中随机遮盖或替换的部分, 其余部分不做损失, 对于其他部分, 模型输出什么东西, 我们不在意.
(2) Next Sentence Predict(NSP)
- 首先我们拿到属于上下文的一对句子, 也就是两个句子, 之后我们要在这两段连续的句子里面加一些特殊
:\([cls]\)上一句话,\([sep]\)下一句话\([sep]\)。
也就是在句子开头加一个, 在两句话之中和句末加
, 具体地就像下图一样:

- 我们看到上图中两句话是
my dog is cute
he likes playing
,
我的狗很可爱
他喜欢玩耍
, 除此之外, 我们还要准备同样格式的两句话, 但他们不属于上下文关系的情况;
我的狗很可爱
企鹅不擅长飞行
, 可见这属于上下句不属于上下文关系的情况;
在实际的训练中, 我们让上面两种情况出现的比例为, 也就是一半的时间输出的文本属于上下文关系, 一半时间不是.
- 我们进行完上述步骤之后, 还要随机初始化一个可训练的
, 见上图中, 作用就是用
的信息让模型分开上下句, 我们一把给上句全
的
, 下句啊全
的
, 让模型得以判断上下句的起止位置, 例如:
我的狗很可爱
企鹅不擅长飞行
上面和
就是
.
- 还记得我们上节课说过的, 注意力机制就是, 让每句话中的每一个字对应的那一条向量里, 都融入这句话所有字的信息, 那么我们在最终隐藏层的计算结果里, 只要取出
所对应的一条向量, 里面就含有整个句子的信息, 因为我们期望这个句子里面所有信息都会往
所对应的一条向量里汇总:
模型最终输出的隐藏层的计算结果的维度是:
我们
我们要取出所对应的一条向量,
对应着
维度的第
条:
之后我们再初始化一个权重, 完成从维度到
的映射, 也就是逻辑回归, 之后用
函数激活, 就得到了而分类问题的推断.
我们用来表示模型的输出的推断, 他的值介于
之间:
\(\hat{y} = sigmoid(Linear(cls\_vector)) \quad \hat{y} \in (0, \ 1)\)
参考内容:
[1] Vaswani A, Shazeer N, Parmar N, et al. Attention is all you need[C]//Advances in neural information processing systems. 2017: 5998-6008.
[2] Devlin J, Chang M W, Lee K, et al. Bert: Pre-training of deep bidirectional transformers for language understanding[J]. arXiv preprint arXiv:1810.04805, 2018.
[3] https://github.com/aespresso/a_journey_into_math_of_ml
BERT模型总结的更多相关文章
- BERT模型在多类别文本分类时的precision, recall, f1值的计算
BERT预训练模型在诸多NLP任务中都取得最优的结果.在处理文本分类问题时,即可以直接用BERT模型作为文本分类的模型,也可以将BERT模型的最后层输出的结果作为word embedding导入到我们 ...
- 从Word Embedding到Bert模型—自然语言处理中的预训练技术发展史(转载)
转载 https://zhuanlan.zhihu.com/p/49271699 首发于深度学习前沿笔记 写文章 从Word Embedding到Bert模型—自然语言处理中的预训练技术发展史 张 ...
- attention、self-attention、transformer和bert模型基本原理简述笔记
attention 以google神经机器翻译(NMT)为例 无attention: encoder-decoder在无attention机制时,由encoder将输入序列转化为最后一层输出state ...
- BERT模型介绍
前不久,谷歌AI团队新发布的BERT模型,在NLP业内引起巨大反响,认为是NLP领域里程碑式的进步.BERT模型在机器阅读理解顶级水平测试SQuAD1.1中表现出惊人的成绩:全部两个衡量指标上全面超越 ...
- 想研究BERT模型?先看看这篇文章吧!
最近,笔者想研究BERT模型,然而发现想弄懂BERT模型,还得先了解Transformer. 本文尽量贴合Transformer的原论文,但考虑到要易于理解,所以并非逐句翻译,而是根据笔者的个人理解进 ...
- zz从Word Embedding到Bert模型—自然语言处理中的预训练技术发展史
从Word Embedding到Bert模型—自然语言处理中的预训练技术发展史 Bert最近很火,应该是最近最火爆的AI进展,网上的评价很高,那么Bert值得这么高的评价吗?我个人判断是值得.那为什么 ...
- 图示详解BERT模型的输入与输出
一.BERT整体结构 BERT主要用了Transformer的Encoder,而没有用其Decoder,我想是因为BERT是一个预训练模型,只要学到其中语义关系即可,不需要去解码完成具体的任务.整体架 ...
- bert模型参数简化
我们下载下来的预训练的bert模型的大小大概是400M左右,但是我们自己预训练的bert模型,或者是我们在开源的bert模型上fine-tuning之后的模型的大小大约是1.1G,我们来看看到底是什么 ...
- BERT模型
BERT模型是什么 BERT的全称是Bidirectional Encoder Representation from Transformers,即双向Transformer的Encoder,因为de ...
- 使用BERT模型生成句子序列向量
之前我写过一篇文章,利用bert来生成token级向量(对于中文语料来说就是字级别向量),参考我的文章:<使用BERT模型生成token级向量>.但是这样做有一个致命的缺点就是字符序列长度 ...
随机推荐
- 谈谈模型融合之一 —— 集成学习与 AdaBoost
前言 前面的文章中介绍了决策树以及其它一些算法,但是,会发现,有时候使用使用这些算法并不能达到特别好的效果.于是乎就有了集成学习(Ensemble Learning),通过构建多个学习器一起结合来完成 ...
- Liquibase 使用(全)
聊一个数据库脚本的版本工具 Liquibase,官网在这里 ,初次看到,挺神奇的,数据库脚本也可以有版本管理,同类型的工具还有 flyway . 开发过程经常会有表结构和变更,让运维来维护的话,通常会 ...
- codeforces -1214 E
题目https://codeforces.com/problemset/problem/1214/E 就是得知奇数之间不产生影响,先造出一条链,再用偶数往里插就行.链要di从大到小排个序呀!! #in ...
- SQL Server 中数据查询注意事项
1.查询语句不用区分大小写,而且即使每张表的表名或者列名出现大写字母,在写查询语句的时候也不用区分大小写,查询结果保持一致,所以查询语句小写即可. 2.在写查询语句的时候列名不需要带单引号,数值型的字 ...
- shopnc 二次开发问题(一)
1.关于shopnc商品详情页面多规格抢购,价格显示都是显示的抢购价格问题 路径: data/model/groupbuy.model.php 方法:getGroupbuyInfoByGoodsCom ...
- AQS 原理以及 AQS 同步组件总结
1 AQS 简单介绍 AQS 的全称为(AbstractQueuedSynchronizer),这个类在 java.util.concurrent.locks 包下面. AQS 是一个用来构建锁和同步 ...
- Linux环境下部署svn服务详解
说明 环境: 操作系统:centos 8.0 IP:39.100.228.13 安装 用ROOT账号登录,在控制台执行以下命令,一直默认安装就好可以了. [root@localhost ~]#yum ...
- 单用户登陆demo-后者挤到前者,类似QQ
单用户登陆demo ,采用的是Tp5. 流程是,当用户首次登陆是验证用户帐号密码,成功的,用当前时间戳加上用户id和ip 拼接成一个标识,暂且sign ,然后存入cookie ,时间戳存入缓存redi ...
- 小技巧(2) 查询自己博客的SEO(如果违规,请先提醒)
今天,教大家查看自己博客的SEO. 首先,上网站http://seo.chinaz.com/ 接着,在网页输入框中输入自己博客地址(带后面路径,不是cnblogs.com这样的,类似https://w ...
- 值得收藏!my.cnf配置文档详解
MySql对于开发人员来说应该都比较熟悉,不管是小白还是老码农应该都能熟练使用.但是要说到的各种参数的配置,我敢说大部分人并不是很熟悉,当我们需要优化mysql,改变某项参数的时候.还是要到处在网上查 ...
