从头学pytorch(六):权重衰减

深度学习中常常会存在过拟合现象,比如当训练数据过少时,训练得到的模型很可能在训练集上表现非常好,但是在测试集上表现不好.

应对过拟合,可以通过数据增强,增大训练集数量.我们这里先不介绍数据增强,先从模型训练的角度介绍常用的应对过拟合的方法.

权重衰减

权重衰减等价于 \(L_2\) 范数正则化（regularization）。正则化通过为模型损失函数添加惩罚项使学出的模型参数值较小，是应对过拟合的常用手段。我们先描述\(L_2\)范数正则化，再解释它为何又称权重衰减。

\(L_2\)范数正则化在模型原损失函数基础上添加\(L_2\)范数惩罚项，从而得到训练所需要最小化的函数。\(L_2\)范数惩罚项指的是模型权重参数每个元素的平方和与一个正的常数的乘积。线性回归一文中的线性回归损失函数

\[\ell(w_1, w_2, b) = \frac{1}{n} \sum_{i=1}^n \frac{1}{2}\left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right)^2
\]

为例，其中\(w_1, w_2\)是权重参数，\(b\)是偏差参数，样本\(i\)的输入为\(x_1^{(i)}, x_2^{(i)}\)，标签为\(y^{(i)}\)，样本数为\(n\)。将权重参数用向量\(\boldsymbol{w} = [w_1, w_2]\)表示，带有\(L_2\)范数惩罚项的新损失函数为

\[\ell(w_1, w_2, b) + \frac{\lambda}{2n} \|\boldsymbol{w}\|^2,
\]

其中超参数\(\lambda > 0\)。当权重参数均为0时，惩罚项最小。当\(\lambda\)较大时，惩罚项在损失函数中的比重较大，这通常会使学到的权重参数的元素较接近0。当\(\lambda\)设为0时，惩罚项完全不起作用。上式中\(L_2\)范数平方\(\|\boldsymbol{w}\|^2\)展开后得到\(w_1^2 + w_2^2\)。

显然,相比没有正则化项的loss,有了\(L_2\)范数惩罚项后求导后将多出来一项\({\lambda}w_i\),所以，在小批量随机梯度下降中，权重\(w_1\)和\(w_2\)的迭代方式将变为

\[\begin{aligned}
w_1 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_1 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_1^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right),\\
w_2 &\leftarrow \left(1- \frac{\eta\lambda}{|\mathcal{B}|} \right)w_2 - \frac{\eta}{|\mathcal{B}|} \sum_{i \in \mathcal{B}}x_2^{(i)} \left(x_1^{(i)} w_1 + x_2^{(i)} w_2 + b - y^{(i)}\right).
\end{aligned}
\]

可见，\(L_2\)范数正则化令权重\(w_1\)和\(w_2\)先自乘小于1的数，再减去不含惩罚项的梯度。因此，\(L_2\)范数正则化又叫权重衰减.

权重衰减通过惩罚绝对值较大的模型参数为需要学习的模型增加了限制，这可能对过拟合有效。实际场景中，我们有时也在惩罚项中添加偏差元素的平方和。

高维线性回归实验

我们创建一个数据集,来模拟过拟合,以及权重衰减针对过拟合的效果.

设数据样本特征的维度为\(p\)。对于训练数据集和测试数据集中特征为\(x_1, x_2, \ldots, x_p\)的任一样本，我们使用如下的线性函数来生成该样本的标签：

\[y = 0.05 + \sum_{i = 1}^p 0.01x_i + \epsilon
\]

其中噪声项\(\epsilon\)服从均值为0、标准差为0.01的正态分布。为了较容易地观察过拟合，我们考虑高维线性回归问题，如设维度\(p=200\)；同时，我们特意把训练数据集的样本数设低，如20。

导入必要的包

import torch

import torch.nn as nn

import numpy as np

数据集创建

n_train, n_test, num_inputs = 20, 100, 200

true_w, true_b = torch.ones(num_inputs, 1) * 0.01, 0.05

features = torch.randn((n_train + n_test, num_inputs))

labels = torch.matmul(features, true_w) + true_b

labels += torch.tensor(np.random.normal(0, 0.01,

                                        size=labels.size()), dtype=torch.float)

train_features, test_features = features[:n_train, :], features[n_train:, :]

train_labels, test_labels = labels[:n_train], labels[n_train:]

dataset = torch.utils.data.TensorDataset(train_features, train_labels)

参数初始化

def init_params():

    w = torch.rand((num_inputs, 1), requires_grad=True)

    b = torch.zeros(1, requires_grad=True)

    return [w, b]

模型定义

def linreg(X, w, b):

    # print(X.dtype,b.dtype)

    return torch.mm(X, w) + b

损失函数定义

由于我们想验证L2正则项的作用,所以需要定义l2_penalty(w),loss由２部分构成,一部分就是正常的均方误差,一部分是

L2正则项,用以控制w的大小. \(\lambda\)则表示这两部分误差的比例.

(y_hat - y.view(y_hat.size())) ** 2 / 2是一个shape为[batch,1]的Ｔensor，(w**2).sum()/2是一个标量,

他们二者相加时,后者会自动扩展成与前者相同shape的张量.

def squared_loss(y_hat, y):

    # 注意这里返回的是向量, 另外, pytorch里的MSELoss并没有除以 2

    return (y_hat - y.view(y_hat.size())) ** 2 / 2

def l2_penalty(w):

    return (w**2).sum()/2

def total_loss(y_hat, y,w,lambd):

    return (y_hat - y.view(y_hat.size())) ** 2 / 2 + lambd * (w**2).sum()/2 #这里用了广播机制

定义优化器

def sgd(params, lr, batch_size):

    for param in params:

        param.data -= lr * param.grad / batch_size # 注意这里更改param时用的param.data

训练

注意,在训练阶段,在反向传播时,我们计算loss时用的是total_loss,即加入了L2正则项的.在推导阶段,计算在训练集/测试集上的loss

用的是squared_loss.

batch_size, num_epochs, lr = 2, 100, 0.003

train_iter = torch.utils.data.DataLoader(dataset,batch_size=batch_size,shuffle=True)

net = linreg

def train(lamda):

    w,b = init_params()

    train_ls, test_ls = [], []

    for epoch in range(num_epochs):

        for X,y in train_iter:

            y_hat = net(X,w,b)

            l = total_loss(y_hat,y,w,lamda).sum()

            #print(w.grad.data)

            if w.grad is not None:

                #print(w.grad.data)

                w.grad.data.zero_()

                b.grad.data.zero_()

            else:

                print("grad 0 epoch %d" % (epoch))

            l.backward()

            sgd([w,b], lr, batch_size)

            #print(l.item())

        train_l = squared_loss(net(train_features,w,b),train_labels)

        print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))

        train_ls.append(train_l.mean().item())

        test_l = squared_loss(net(test_features,w,b),test_labels)

        print('epoch %d, loss %f' % (epoch + 1, test_l.mean().item()))

        test_ls.append(test_l.mean().item())

    d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',

                 range(1, num_epochs + 1), test_ls, ['train', 'test'])

当train(0)时,即相当于不带正则项的loss．绘制出的曲线如下:

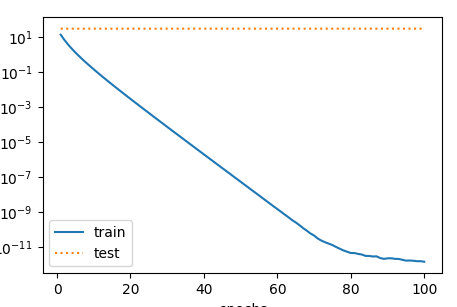
当train(1)时,即相当于squared_loss和L2正则项为1:1,绘制出的曲线如下：

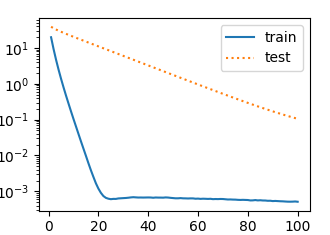
以上是我们手动实现了损失函数,优化器等．用torch里封装好的MSELoss,optim等实现如下:

def train_use_torch(wd):

    net = torch.nn.Linear(num_inputs,1)

    loss = nn.MSELoss()

    nn.init.normal_(net.weight,mean=0,std=1)

    nn.init.normal_(net.bias,mean=0,std=1)

    optimizer_w =torch.optim.SGD(params=[net.weight],lr=lr,weight_decay=wd) #权重衰减

    optimizer_b =torch.optim.SGD(params=[net.bias],lr=lr) #偏差参数衰减

    train_ls, test_ls = [], []

    for epoch in range(num_epochs):

        for X,y in train_iter:

            y_hat = net(X)

            l = loss(y_hat,y).sum()

            optimizer_w.zero_grad()

            optimizer_b.zero_grad()

            l.backward()

            optimizer_w.step()

            optimizer_b.step()

        train_l = squared_loss(net(train_features),train_labels)

        print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))

        train_ls.append(train_l.mean().item())

        test_l = squared_loss(net(test_features),test_labels)

        print('epoch %d, loss %f' % (epoch + 1, test_l.mean().item()))

        test_ls.append(test_l.mean().item())

    d2l.semilogy(range(1, num_epochs + 1), train_ls, 'epochs', 'loss',

                 range(1, num_epochs + 1), test_ls, ['train', 'test'])

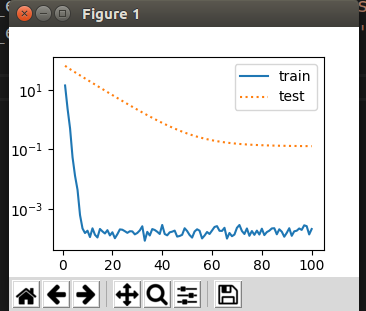
对不同的参数,我们用不同的optimizer实例,w需要衰减,b不需要.

    optimizer_w =torch.optim.SGD(params=[net.weight],lr=lr,weight_decay=wd) #权重衰减

    optimizer_b =torch.optim.SGD(params=[net.bias],lr=lr) #偏差参数衰减

```　

同样的,在更新参数时,需要对两个optimizer实例都调用

optimizer_w.step()

optimizer_b.step()

最终绘制效果如下:

![](https://img2018.cnblogs.com/blog/583030/201912/583030-20191228202722178-992077842.png)