关于电容与Q值

1, 电容模型

电容阻抗可以表示为：

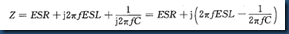
可算得自谐振频率点为：

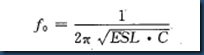
在该点，容抗与感抗差为0，电容表现出纯电阻性。

2, 阻抗曲线

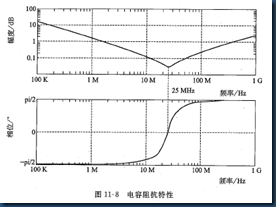
自谐点是区分电容器呈容性还是感性的分界点。从阻抗曲线看，在自谐点附近阻抗较小，因此去耦电容都有一定的工作范围，只有在自谐点附近电容才有较好的去耦作用。

3, Q值

因为电容可以等效为RLC串行电路， 因此它也会存在品质因素，即Q值。

RLC串联电路Q值定义为谐振时感抗（容抗）与串联电阻的比值：

可见Q值仅与电路参数有关，与工作频率无关。

4, Q值与滤波

Q值与电路频率选择性密切相关。

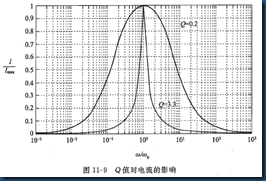
Q值越大，单位电流变化内允许的频率偏移越小，频率选择性越高。

板级电源滤波时，我们希望去耦范围稍为宽一些，因此会在电源端放置一些Q值稍小的电容。

下图是Q值为3.3的10uF钽电容和Q值为0.2的0.01uF陶瓷电容的Q值和阻抗曲线对照图。

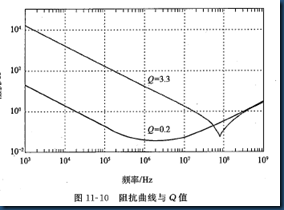
顺便提一句，一般来说陶瓷电容的ESR要比钽电容的要小；ESR越大，电源纹波上越倾向出现一个三角波。