主题模型（概率潜语义分析PLSA、隐含狄利克雷分布LDA）

一、pLSA模型

1、朴素贝叶斯的分析

（1）可以胜任许多文本分类问题。
（2）无法解决语料中一词多义和多词一义的问题——它更像是词法分析，而非语义分析。
（3）如果使用词向量作为文档的特征，一词多义和多词一义会造成计算文档间相似度的不准确性。
（4）可以通过增加“主题”的方式，一定程度的解决上述
问题：一个词可能被映射到多个主题中（一词多义），多个词可能被映射到某个主题的概率很高（多词一义）

2.pLSA模型

基于概率统计的pLSA模型(probabilistic latentsemantic analysis, 概率隐语义分析)，增加了主题模型，形成简单的贝叶斯网络，可以使
用EM算法学习模型参数。

（1）D代表文档，Z代表主题(隐含类别)，W代表单词；P(d i )表示文档d i 的出现概率， P(z k |d i )表示文档d i 中主题z k 的出现概率， P(w j |z k )表示给定主题z k 出现单词w j 的概率。

（2）每个主题在所有词项上服从多项分布，每个文档在所有主题上服从多项分布。

（3）整个文档的生成过程是这样的： 以P(d i )的概率选中文档d i ； 以P(z k |d i )的概率选中主题z k ； 以P(w j |z k )的概率产生一个单词w j

观察数据为(d i ,w j )对，主题z k 是隐含变量。 (d i ,w j )的联合分布为

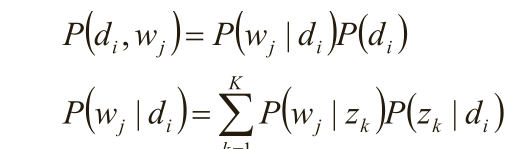
而 对应了两组多项分布，而计算每个文档的主题分布，就是该模型的任务目标。

(4)极大似然估计：w j 在d i 中出现的次数n(di,wj)

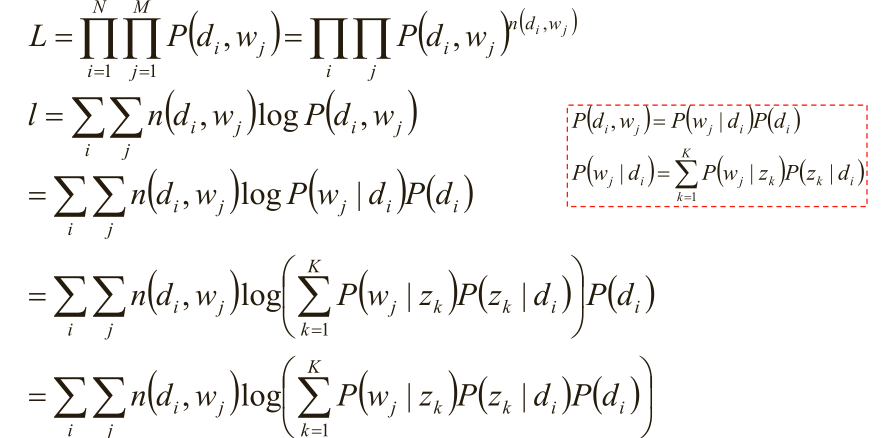
(5)使用逐次逼近的办法：
假定P(z k |d i )、P(w j |z k )已知，求隐含变量z k 的后验概率；
 在(d i ,w j ,z k )已知的前提下，求关于参数P(z k |d i )、P(w j |z k )的似然函数期望的极大值，得到最优解P(z k |d i )、P(w j |z k ) ，带入上一步，从而循环迭代；

隐含变量z k 的后验概率；

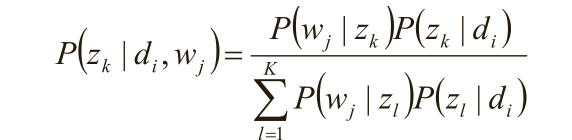
在(d i ,w j ,z k )已知的前提下，求关于参数P(z k |d i )、P(w j |z k ) 的似然函数期望的极大值，得到最优解P(z k |d i )、P(w j |z k ) ，带入上一步，从而循环迭代；

(6)分析似然函数期望
在(d i ,w j ,z k )已知的前提. 在(d i ,w j ,z k )已知的前提下，求关于参数P(z k |d i )、P(w j |z k ) 的似然函数期望的极大值，得到最优解P(z k |d i )、P(w j |z k ) ，带入上一步，从而循环迭代

分析似然函数期望:

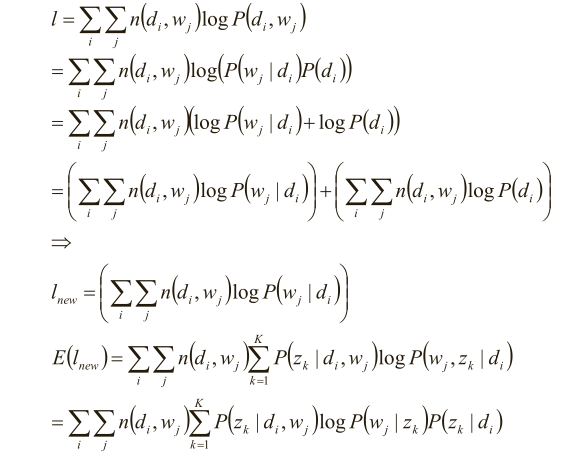
(7)完成目标函数的建立

关于参数P(z k |d i )、P(w j |z k ) 的函数E，并且，带有概率加和为1的约束条件：

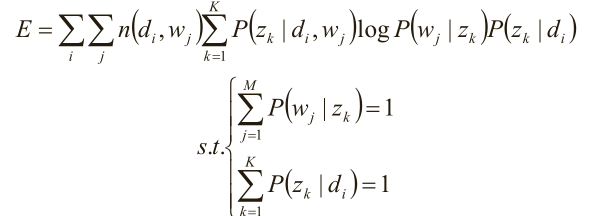
显然，这是只有等式约束的求极值问题，使用Lagrange乘子法解决。

求驻点：

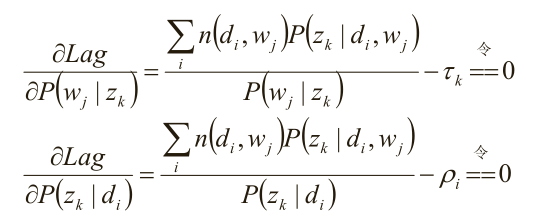
分析第一个等式

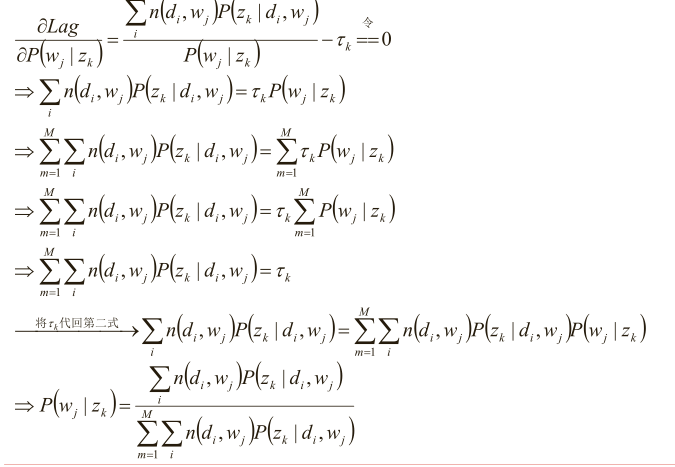
同理分析第二个等式

最后就是下面两步的迭代了，也是实现算法的主要步骤了

求极值时的解——M-Step：

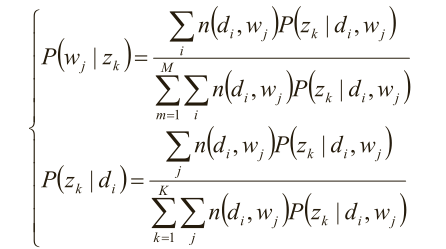
别忘了E-step：：

（8）pLSA的总结

1）pLSA应用于信息检索、过滤、自然语言处理等领域，pLSA考虑到词分布和主题分布，使用EM算法来学习参数。
2） 虽然推导略显复杂，但最终公式简洁清晰，很符合直观理解，需用心琢磨；此外，推导过程使用了EM算法，也是学习EM算法的重要素材。

二、LDA

（1）共轭先验分布

1）由于x为给定样本，P(x)有时被称为“证据”，仅仅是归一化因子，如果不关心P(θ|x)的具体值，只考察θ取何值时后验概率P(θ|x)最大，则可将分母省去。

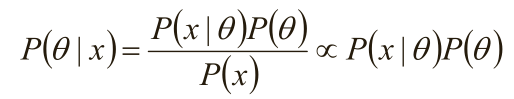
在贝叶斯概率理论中，如果后验概率P(θ|x)和先验概率p(θ)满足同样的分布律，那么，先验分布和后验分布被叫做共轭分布，同时，先验分布叫做似然函数的共轭先验分布。

2）共轭先验分布的实践意义

似然函数P(x|θ)表示以先验θ为参数的概率分布，可以直接求得。 先验分布P(θ)是θ的分布率，可根据先验知识获得。

方案：选取似然函数P(x|θ)的共轭先验作为P(θ)的分布，这样，P(x|θ)乘以P(θ) (然后归一化)得到的P(θ|x)的形式和P(θ)的形式一样。

（2）Dirichlet分布

1) Dirichlet分布的定义：

2)Dirichlet分布分析

α是参数向量，共K个；定义在x 1 ,x 2 …x K-1 维上：x 1 +x 2 +…+x K-1 +x K =1，x 1 ,x 2 …x K-1 >0，定义在(K-1)维的单纯形上，其他区域的概率密度为0

3）对称Dirichlet分布

          

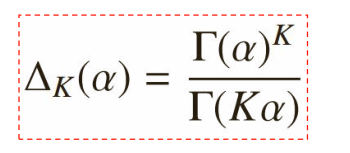
α=1时，退化为均匀分布；

当α>1时， p 1 =p 2 =…=p k 的概率增大

当α<1时， p i =1，p 非i =0的概率增大

（3）LDA的解释

1）共有m篇文章，一共涉及了K个主题；每篇文章(长度为N m )都有各自的主题分布，主题分布是多项分布，该多项分布的参数服从Dirichlet分布，该Dirichlet分布的参数为α；

每个主题都有各自的词分布，词分布为多项分布，该多项分布的参数服从Dirichlet分布，该Dirichlet分布的参数为 β。对于某篇文章中的第n个词，首先从该文章的主题分布中采样一个主题，然后在这
个主题对应的词分布中采样一个词。不断重复这个随机生成过程，直到m篇文章全部完成上述过程。

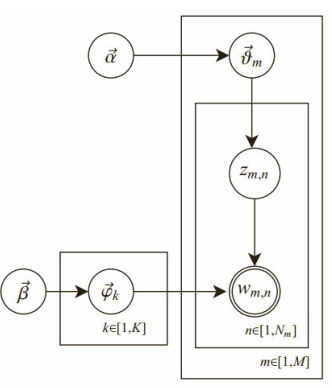
2）参数的学习

给定一个文档集合，w mn 是可以观察到的已知变量，α和β是根据经验给定的先验参数，其他的变量z mn 、θ、φ都是未知的隐含变量，需要根据观察到的变量来学习估计的。根据LDA的图模型，可以写出所有变量
的联合分布：

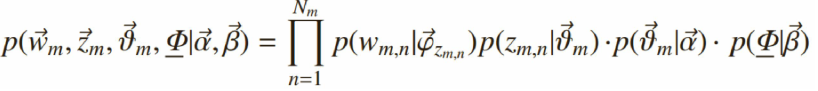
3)似然概率

一个词w mn 初始化为一个词t的概率是:

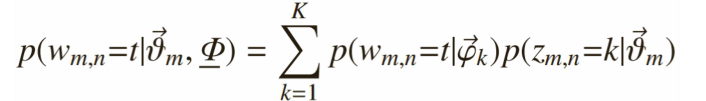
每个文档中出现主题k的概率乘以主题k下出现词t的概率，然后枚举所有主题求和得到。整个文档集合的似然函数为：

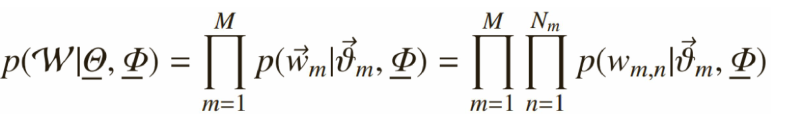
4)Gibbs Sampling

a.Gibbs Sampling算法的运行方式是每次选取概率向量的一个维度，给定其他维度的变量值采样当前维度的值。不断迭代，直到收敛输出待估计的参数。

b.初始时随机给文本中的每个词分配主题z (0) ，然后统计每个主题z下出现词t的数量以及每个文档m下出现主题z的数量，每一轮计算p(z i |z -i ,d,w)，即排除当前词的主题分布：根据其他所有词的主题分布估计当前词分配各个主题的概率。

c.当得到当前词属于所有主题z的概率分布后，根据这个概率分布为该词采样一个新的主题。

d.用同样的方法更新下一个词的主题，直到发现每个文档的主题分布θ i 和每个主题的词分布φ j 收敛，算法停止，输出待估计的参数θ和φ，同时每个单词的主题z mn 也可同时得出。

e.实际应用中会设置最大迭代次数。每一次计算p(zi|z -i ,d,w)的公式称为Gibbs updating rule。