拉格朗日插值法——用Python进行数值计算

插值法的伟大作用我就不说了。。。。

那么贴代码？

首先说一下下面几点：

1. 已有的数据样本被称之为 “插值节点”

2. 对于特定插值节点，它所对应的插值函数是必定存在且唯一的（关于这个的证明我暂时不说了，如果哪天我回头看看我的blog有点寒碜，我再再补上）

　　也就是说对于同样的插值样本来说，用不同方法求得的插值函数本质上其实是一样的。

3. 拉格朗日插值法依赖于每个插值节点对应的插值基函数，也就是说每个插值节点都有对应的插值基函数。

4. 拉格朗日插值函数最终由所有插值节点中每个插值节点的纵坐标值与它对应的插值函数的积的和构成。

5. 也就是说拉格朗日插值法关键在于求基函数

6. 拉格朗日插值法并不好，当每一次加入新的插值节点的时候，所有的系数都要重算一遍

计算插值函数参数的最本质的方法是解下面的矩阵方程：

我先构造一组插值样本：

sr_x = [i for i in range(-50, 50, 10)]
sr_fx = [i**2 for i in sr_x]

　　sr_x 为样本的横坐标，sr_fx为样本的纵坐标，样本的定义域是[-50, 50]，样本之间距离为10

　　纵坐标为横坐标的平方，也就是说这是一个二次函数 sr_fx = sr_x ^2

这样一组样本的图像是这样的：

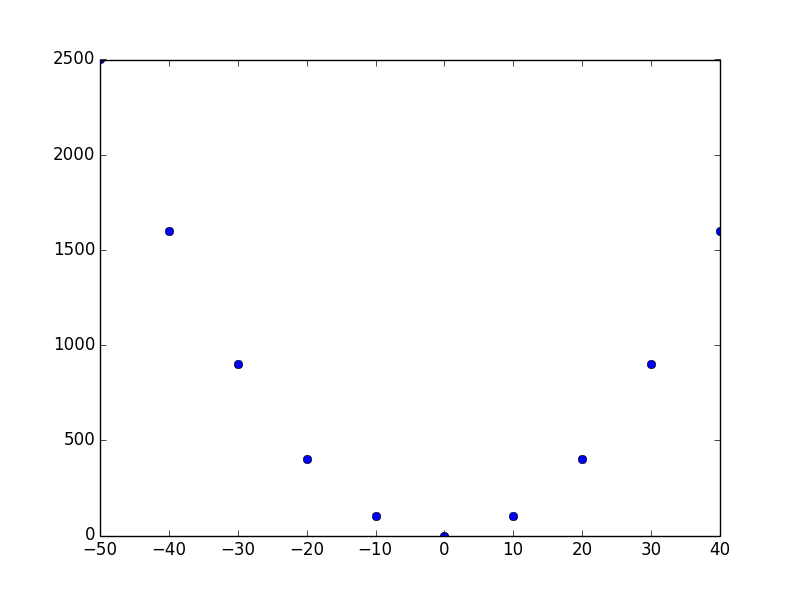
然后我用这一组插值节点来获得每个节点对应的插值基函数：

基函数的计算公式是 li = (x - x0)(x - x1) ... (x - x(i-1))(x - x(i+1)) ... (x - xn)/(xi - x0)(xi - x1) ... (xi - x(i-1))(xi - x(i+1)) ... (xi - xn)

其中W = (x - x0)(x - x1) ... (x - x(i-1))(x - x(i+1)) ... (x - xn)

　　c = (xi - x0)(xi - x1) ... (xi - x(i-1))(xi - x(i+1)) ... (xi - xn)

因此 li = W / c

注意：在计算i的插值基函数的时候，公式c与W里面是没有被减数为Xi项的。（要是有的话W与c就为0了）

这一段代码是这样的：

def get_li(xi, x_set = []):
    def li(Lx):
        W = 1; c = 1
        for each_x in x_set:
            if each_x == xi:
                continue
            W = W * (Lx - each_x)

        for each_x in x_set:
            if each_x == xi:
                continue
            c = c * (xi - each_x)

        # 这里一定要转成float类型，否则极易出现严重错误. 原因就不说了
        return W / float(c)
    return li

这段代码用到了闭包，这样可以返回一个基函数，并且这个函数以get_li的内部为上下文（上下文这个翻译总让人感觉怪怪的，似乎与写作文有某种联系）。

当获得基函数之后就是累加基函数与插值节点纵坐标的乘积构成拉格朗日插值函数了

这一段的代码是这样：

"""
@brief: 获得拉格朗日插值函数
@param: x       插值节点的横坐标集合
@param: fx      插值节点的纵坐标集合
@return: 参数所指定的插值节点集合对应的插值函数
"""
def get_Lxfunc(x = [], fx = []):
    set_of_lifunc = []
    for each in x:  # 获得每个插值点的基函数
        lifunc = get_li(each, x)
        set_of_lifunc.append(lifunc)    # 将集合x中的每个元素对应的插值基函数保存

    def Lxfunc(Lx):
        result = 0
        for index in range(len(x)):
            result = result + fx[index]*set_of_lifunc[index](Lx)    #根据根据拉格朗日插值法计算Lx的值
            print fx[index]
        return result

    return Lxfunc

　　到这里就大功告成了，我用上面给的插值节点计算出的插值函数是这样的：

完整代码如下：

# -*- coding: utf-8 -*-
"""
Created on Wed Nov 16 13:26:58 2016

@author: tete
@brief: 拉格朗日插值法
"""

import matplotlib.pyplot as plt

"""
@brief: 获得拉格朗日插值基函数
@param: xi      xi为第i个插值节点的横坐标
@param: x_set   整个插值节点集合
@return: 返回值为参数xi对应的插值基函数
"""
def get_li(xi, x_set = []):
    def li(Lx):
        W = 1; c = 1
        for each_x in x_set:
            if each_x == xi:
                continue
            W = W * (Lx - each_x)

        for each_x in x_set:
            if each_x == xi:
                continue
            c = c * (xi - each_x)

        # 这里一定要转成float类型，否则极易出现严重错误. 原因就不说了
        return W / float(c)
    return li

"""
@brief: 获得拉格朗日插值函数
@param: x       插值节点的横坐标集合
@param: fx      插值节点的纵坐标集合
@return: 参数所指定的插值节点集合对应的插值函数
"""
def get_Lxfunc(x = [], fx = []):
    set_of_lifunc = []
    for each in x:  # 获得每个插值点的基函数
        lifunc = get_li(each, x)
        set_of_lifunc.append(lifunc)    # 将集合x中的每个元素对应的插值基函数保存

    def Lxfunc(Lx):
        result = 0
        for index in range(len(x)):
            result = result + fx[index]*set_of_lifunc[index](Lx)    #根据根据拉格朗日插值法计算Lx的值
            print fx[index]
        return result

    return Lxfunc

"""
demo:
"""
if __name__ == '__main__':   

    ''' 插值节点, 这里用二次函数生成插值节点，每两个节点x轴距离位10 '''
    sr_x = [i for i in range(-50, 50, 10)]
    sr_fx = [i**2 for i in sr_x]

    Lx = get_Lxfunc(sr_x, sr_fx)            # 获得插值函数
    tmp_x = [i for i in range(-45, 45)]     # 测试用例
    tmp_y = [Lx(i) for i in tmp_x]          # 根据插值函数获得测试用例的纵坐标

    ''' 画图 '''
    plt.figure("play")
    ax1 = plt.subplot(111)
    plt.sca(ax1)
    plt.plot(sr_x, sr_fx, linestyle = ' ', marker='o', color='b')
    plt.plot(tmp_x, tmp_y, linestyle = '--', color='r')
    plt.show()