逻辑回归(分类问题)(Logistic Regression、罗杰斯特回归)

1. 逻辑回归：问题只有两项，即{0, 1}。一般而言，回归问题是连续模型，不用在分类问题上，且噪声较大，但如果非要引入，那么采用逻辑回归模型。

对于一般训练集：

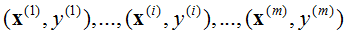
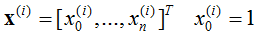
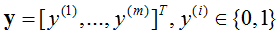
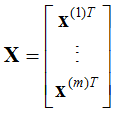
参数系统为：

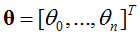
逻辑回归模型为：

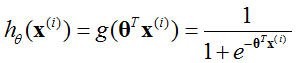     (sigmoid函数)

    

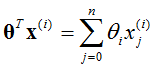
1. 参数求解

对于逻辑回归用来分类{0, 1}问题，假设满足伯努利模型：

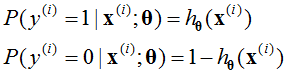
可以将上式写为一般形式为：

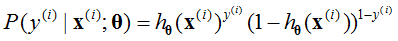
为了得到参数θ，求最大似然估计[2]，可以得到:

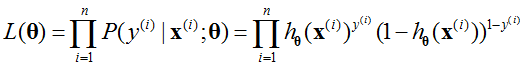
为了简化问题，采用ln函数，即对数似然，可以得到：

这里为了最大似然估计使参数最大化，有两种方法求解：

1. 采用梯度上升的方法(与梯度下降类似，不过减号变为加号)，即：

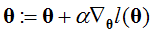(批量梯度上升)

对于每一个θj，可以得到：

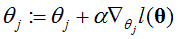(随机梯度上升)

根据l(θ)，有：

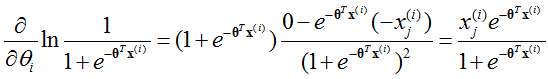
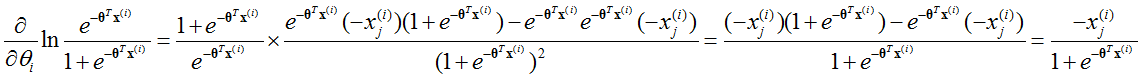
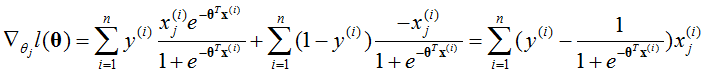
所以：

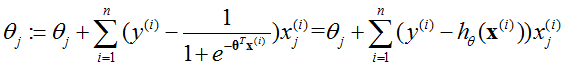
1. 采用牛顿的方法

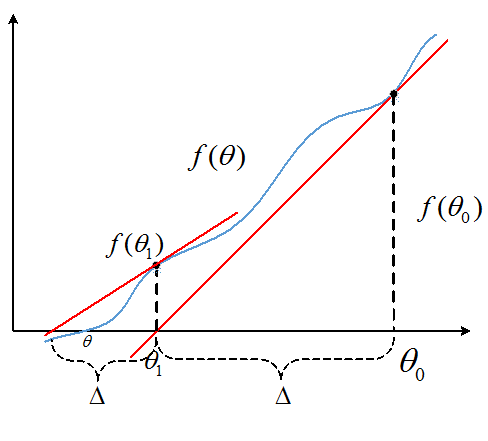
上图目标是找到f(θ)=0，所以用一个迭代的方法，从上图可以看出：

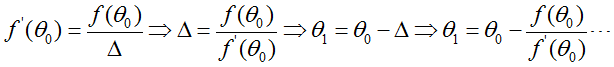
最终找到θ使得f(θ)=0。采用最大似然估计使参数最大，实际上就是找到θ使得l'(θ)=0。那么可以将上式改写为：

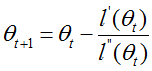
扩展到θ，有：

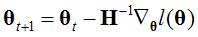
其中，H是Hession矩阵，

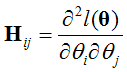
牛顿法是二次收敛，假设第一次迭代精度为0.01error，那么第二次0.001，第三次为0.00001。收敛速度明显高于梯度下降。可是每次需要求一次H矩阵的逆，代价很高。

求最大值时，用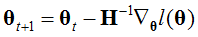，求最小值时实际上也是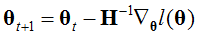，原因个人认为无论时求最大或者最小值都是使得l'(θ)=0，并没有本质变化。

1. 说明：

一件事情的几率可以定义为：

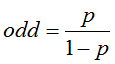
其中，p为改事件发生的概率。那么对数几率logit可以定义为：

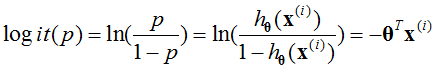
所以，对于logistic回归是对数线性回归。

1. sigmoid函数推导

如果满足对数线性，则有

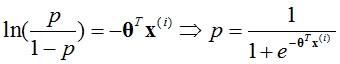
也就是说，sigmoid函数输出的值可以认为是为1类别的概率。

1. logistic回归的损失函数

由于对数似然(logarithm likelihood, LL)是要取最大值，损失函数要求最小，所以对对数似然函数求相反数，即：

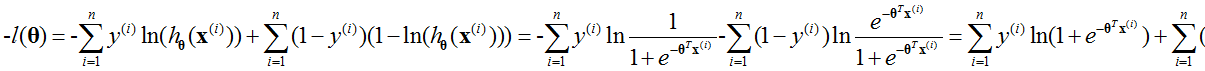
上式是建立在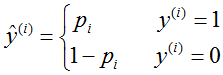，情况下的。

如果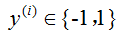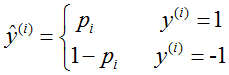，，那么似然函数可以定义为：

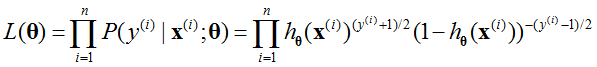
其中指数部分还要满足[0,1]的范围内。那么损失函数(负对数似然函数) 可以写为：

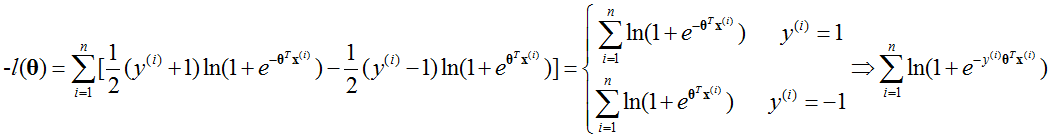
[1]网易公开课——斯坦福大学机器学习

[2] http://blog.csdn.net/yanqingan/article/details/6125812

**转载请注明出处！