Educational Codeforces Round 10 D. Nested Segments 【树状数组区间更新 + 离散化 + stl】

任意门：http://codeforces.com/contest/652/problem/D

D. Nested Segments

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given n segments on a line. There are no ends of some segments that coincide. For each segment find the number of segments it contains.

Input

The first line contains a single integer n (1 ≤ n ≤ 2·105) — the number of segments on a line.

Each of the next n lines contains two integers li and ri ( - 109 ≤ li < ri ≤ 109) — the coordinates of the left and the right ends of the i-th segment. It is guaranteed that there are no ends of some segments that coincide.

Output

Print n lines. The j-th of them should contain the only integer aj — the number of segments contained in the j-th segment.

Examples

input

Copy

4
1 8
2 3
4 7
5 6

output

Copy

3
0
1
0

input

Copy

3
3 4
1 5
2 6

output

Copy

0
1
1

题意概括：

有 N 个区间，求每个区间有多少个存在的子区间。

例如第一个样例：

4
1 8
2 3
4 7
5 6

【1，8】有 3 个，他们发别是 【2，3】，【4，7】，【5，6】；
【2，3】没有；
【4，7】有 1 个，【5，6】；【5，6】没有；

注意：

一、只是有部分相交的区间不在考虑范围内，模拟一下样例二就明白了。

3
3 4
1 5
2 6

二、端点不重合，这个很重要！！！

解题思路：

由题意可知这是离线操作，涉及区间查询和修改，线段树或树状数组。

其次数据范围不小，要考虑离散化。

这道题如何离散化？

二维 pair 储存原数据 + vector 排序&&去重；

树状数组要维护一些什么呢？我们怎么记录区间内有几个符合条件的线段呢？

一开始自己模拟样例一后是想到标记左端点，然后求其区间和，刚好区间和 减去他自己就是答案，不够这种想法是很片面的。

因为有只有部分相交的情况：例如样例二

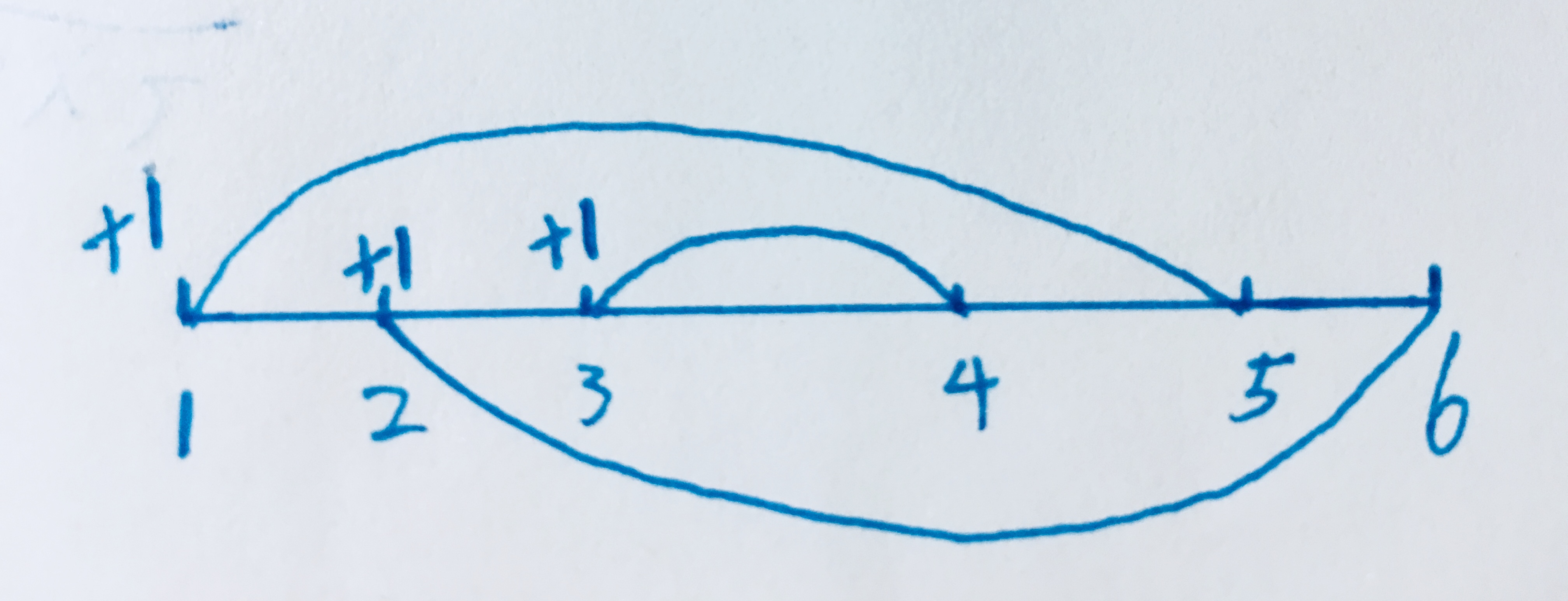
【1，5】= 1+1+1-1 = 2 答案错误（把部分相交的考虑进去了）

但这道题的解决方法就是标记一个端点，如果标记左端点则按右端点顺序遍历，如果标记右端点则按左端点顺序遍历。

固定其中一个端点后求区间和，并且在查询完毕之后要消除当前区间对后面区间的影响，因为我们按照其中一个端点的顺序遍历，如果不消除当前固定端点区间的影响，那么后面就会有部分相交了。

例如说我标记左端点，按照右端点的顺序遍历，如果我遍历右端点为 6 之后没有把【2， 6】的影响消除，那么当我遍历到右端点为 5 的时候就会把只有部分相交的区间也记录进去了。

解决了以上两个大问题，剩下的就是代码实现的事了。

AC code：

 #include <cstdio>
 #include <iostream>
 #include <cstring>
 #include <algorithm>
 #include <cmath>
 #include <map>
 #include <vector>
 #define INF 0x3f3f3f3f
 #define LL long long
 using namespace std;
 const int MAXN = 4e5+;

 int t[MAXN];                            //树状数组
 pair< pair<int, int>, int> p[MAXN];     //记录区间左右端点和
 vector<int> Q;
 map<int, int> mmp;
 int ans[MAXN];
 int N;

 int lowbit(int x){return x&(-x);}
 void Update(int x, int val)
 {
     for(int i = x; i < MAXN; i+=lowbit(i)){
         t[i]+=val;
     }
 }

 int query(int x)
 {
     int res = ;
     for(int i = x; i; i-=lowbit(i))
         res+=t[i];
     return res;
 }

 int main()
 {
     scanf("%d", &N);
     for(int i = ; i <= N; i++){
         scanf("%d %d", &p[i].first.first, &p[i].first.second);
         Q.push_back(p[i].first.first);
         Q.push_back(p[i].first.second);
         p[i].second = i;
     }
     sort(Q.begin(), Q.end());                           //离散化
     Q.erase(unique(Q.begin(),Q.end()), Q.end());        //去重
     for(int i = ; i < Q.size(); i++){
         mmp[Q[i]] = i+;                                //新旧端点的映射关系
     }
     for(int i = ; i <= N; i++){
         p[i].first.first = mmp[p[i].first.first];       //更新区间的左右端点
         p[i].first.second = mmp[p[i].first.second];
         Update(p[i].first.second, );                   //更新区间！！！精妙之处在于标记的该区间的其中一个端点！！！（题目条件端点不重合）
     }
     sort(p+, p++N);                                     //排序等级：左端点 ＞ 右端点 ＞ 区间编号
     for(int i = , j = ; i < MAXN; i++){                 //遍历左端点,注意范围是 1~MAXN
         while(j <= N && p[j].first.first == i){         //左端点相同的区间
             ans[p[j].second] = query(p[j].first.second);
             Update(p[j].first.second, -);              //消除当前区间对后面区间的影响
             j++;
         }
         if(j == N+) break;     //遍历完成
     }
     for(int i = ; i <= N; i++)
         printf("%d\n", ans[i]-);
     return ;
 }