• 注意：需要提前获取到物理机对应的网卡的MAC地址，例如我这里使用虚拟机进行演示

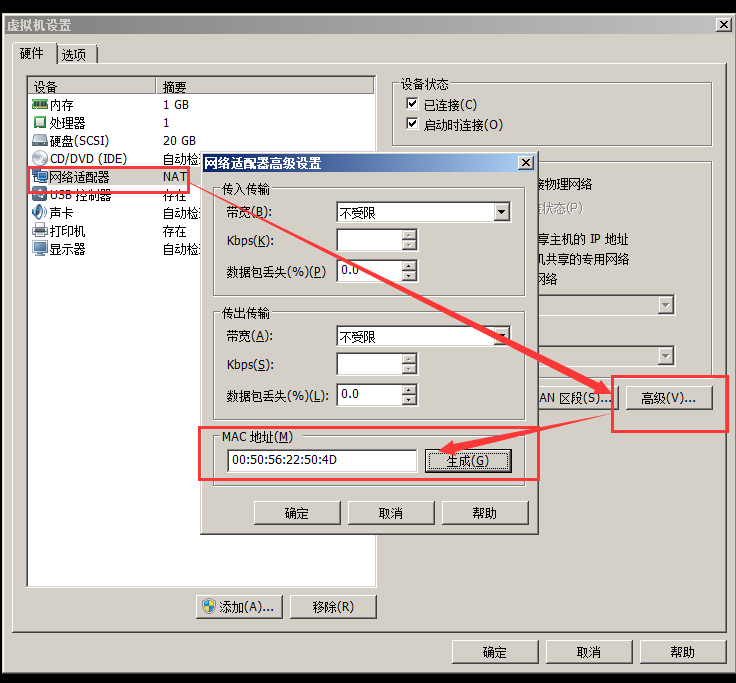
cobbler system add --name=linux-node2.com --mac=00:50:56:22:50:4D --profile=CentOS-7-x86_64 \

 --ip-address=192.168.92.131 --subnet=255.255.255.0 gateway=192.168.92.2 \

--interface=eth0 --static=1 --hostname=linux-node2.com --name-servers="114.114.114.114" \

 --kickstart=/var/lib/cobbler/kickstarts/centos7.ks


这里主要配置主机名，ip地址，掩码，网管，dns，镜像版本
  • 验证执行：
cobbler system list

cobbler sync
  • 验证：发现没有问题

（五）cobbler自定义系统安装的更多相关文章

  1. cobbler 无人值守系统安装

    概述 本文适合centos6 | centos7 系统的安装 执行操作之前:检查系统防火墙,selinux是否关闭,网络链接是否畅通. Cobbler是一个免费开源系统安装部署软件,用于自动化网络安装 ...

  2. SpringBoot入门（五）——自定义配置

    本文来自网易云社区 大部分比萨店也提供某种形式的自动配置.你可以点荤比萨.素比萨.香辣意大利比萨,或者是自动配置比萨中的极品--至尊比萨.在下单时,你并没有指定具体的辅料,你所点的比萨种类决定了所用的 ...

  3. Android UI 绘制过程浅析（五）自定义View

    前言 这已经是Android UI 绘制过程浅析系列文章的第五篇了,不出意外的话也是最后一篇.再次声明一下,这一系列文章,是我在拜读了csdn大牛郭霖的博客文章<带你一步步深入了解View> ...

  4. Volley（五）—— 自定义Request

    详细解读Volley(四)—— 自定义Request Volley中提供了几个Request,如果我们有特殊的需求,完全可以自定义Request的,自定义Request自然要继承Request,那么本 ...

  5. C#微信公众号开发 -- （五）自定义菜单创建

    公众号中,底部都是有自己定义的功能按钮,通过点击某个按钮来实现指定的业务逻辑操作. 下面就来说说这些按钮是怎样放到微信公众平台的,还是先来看看微信的官方解释: 请注意: 1.自定义菜单最多包括3个一级 ...

  6. 【Spring Security】五、自定义过滤器

    在之前的几篇security教程中,资源和所对应的权限都是在xml中进行配置的,也就在http标签中配置intercept-url,试想要是配置的对象不多,那还好,但是平常实际开发中都往往是非常多的资 ...

  7. Spring Security教程(五)：自定义过滤器从数据库从获取资源信息

    在之前的几篇security教程中,资源和所对应的权限都是在xml中进行配置的,也就在http标签中配置intercept-url,试想要是配置的对象不多,那还好,但是平常实际开发中都往往是非常多的资 ...

  8. cobbler 自定义安装系统

    1.自定义安装系统(根据mac地址)--name=定义名称--mac=客户端的mac地址--ip-address=需求的ip--subnet=掩码 --gateway=网关--interface=网口 ...

  9. Cobbler自定义安装系统和私有源

    1.自定义安装系统(根据mac地址) --name=定义名称 --mac=客户端的mac地址 --ip-address=需求的ip --subnet=掩码 --gateway=网关 --interfa ...

随机推荐

  1. 简单配置 Tomcat 的 Server.xml（war包发布）

    <Connector connectionTimeout="20000" port="8080" protocol="HTTP/1.1" ...

  2. Java学习全攻略-->阅读官方文档

    一直感觉Java的官方文档有些杂乱,最近特意整理了一下,仅供参考. 入口 Oracle官方文档入口:http://docs.oracle.com/.下级页面这边只整理了JavaEE跟JavaSE的文档 ...

  3. POJ——2449 Remmarguts' Date

    Description "Good man never makes girls wait or breaks an appointment!" said the mandarin ...

  4. 【转】Word单引号‘’替换为正确的单引号（plsql参数的单引号）

    转自 http://jingyan.baidu.com/article/39810a23db44b5b636fda6f2.html 问题描述:   单引号明显不一样,替换不了 解决方案,如下图

  5. 洛谷 P3203 [HNOI2010]弹飞绵羊 解题报告

    P3203 [HNOI2010]弹飞绵羊 题目描述 某天,Lostmonkey发明了一种超级弹力装置,为了在他的绵羊朋友面前显摆,他邀请小绵羊一起玩个游戏.游戏一开始,Lostmonkey在地上沿着一 ...

  6. mobx基本概念

    mobx是一个简单可扩展的状态管理库,主要用来管理状态之间的依赖关系,可以使用在任何状态管理的场景,并不仅限于react. 结合mobx-react可以用在react中,结合mobx-vue可以用在v ...

  7. python3创建目录

    感觉python3最好用的创建目录函数是os.makedirs,它可以设置在多级目录不存在时自动创建,已经存在也不抛出异常. import os os.makedirs('hello/hello1/h ...

  8. Codeforces Round #524 (Div. 2) B. Margarite and the best present

    B. Margarite and the best present 题目链接:https://codeforces.com/contest/1080/problem/B 题意: 给出一个数列:an=( ...

  9. AtCoder Regular Contest 082 E

    Problem Statement You are given N points (xi,yi) located on a two-dimensional plane. Consider a subs ...

  10. bzoj1503 郁闷的出纳员 splay版

    自己yy的写法 可能有点奇怪吧 详情看代码 还是蛮短的 #include<cstdio> #include<cstring> #include<algorithm> ...