URAL 2034 : Caravans
Description
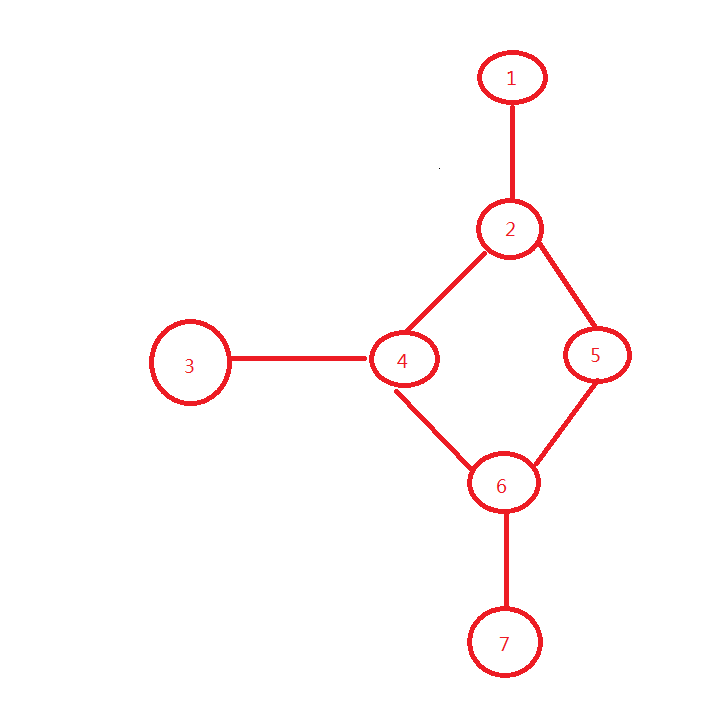
Input
Output
| input | output |
|---|---|
7 7 |
2 |
#include <cstdio>
#include <vector>
#include <queue>
#include <cstring>
using namespace std;
const int maxn = 1e5 + ;
#define max(x,y) ((x)>(y)?(x):(y))
#define min(x,y) ((x)<(y)?(x):(y))
vector<int>e[maxn];
int dp[maxn] , d[maxn] , maxv[maxn], n , m , s , f , r , used[maxn] ;
queue<int>q; void solve()
{
memset(dp , , sizeof(dp));memset(d,-,sizeof(d));memset(maxv,-,sizeof(maxv));memset(used,,sizeof(used));
d[f] = ;
q.push(f);
while(!q.empty())
{
int x = q.front();q.pop();
for(int i = ; i < e[x].size() ; ++ i)
{
int v = e[x][i];
if (d[v] == -)
{
d[v] = d[x] + ;
q.push(v);
}
}
}
maxv[r] = ;
q.push(r);
while(!q.empty())
{
int x = q.front();q.pop();
for(int i = ; i < e[x].size() ; ++ i)
{
int v = e[x][i];
if (maxv[v] == -)
{
maxv[v] = maxv[x] + ;
q.push(v);
}
}
}
dp[s] = maxv[s];used[s] = ;
q.push(s);
while(!q.empty())
{
int x = q.front();q.pop();
maxv[x] = min(maxv[x],dp[x]);
for(int i = ; i < e[x].size() ; ++ i)
{
int v = e[x][i];
if (d[x] - d[v] == )
{
dp[v] = max(dp[v],maxv[x]);
if (!used[v])
{
q.push(v);
used[v] = ;
}
}
}
}
printf("%d\n",maxv[f]);
} int main(int argc,char *argv[])
{
scanf("%d%d",&n,&m);
while(m--)
{
int u ,v ;
scanf("%d%d",&u,&v);u--,v--;
e[u].push_back(v);e[v].push_back(u);
}
scanf("%d%d%d",&s,&f,&r);s--,f--,r--;
solve();
return ;
}
URAL 2034 : Caravans的更多相关文章
- URAL 2034 Caravans(变态最短路)
Caravans Time limit: 1.0 secondMemory limit: 64 MB Student Ilya often skips his classes at the unive ...
- URAL
URAL 2035 输入x,y,c, 找到任意一对a,b 使得a+b==c&& 0<=a<=x && 0<=b<=y 注意后两个条件,顺序搞错 ...
- hdu 2034人见人爱A-B
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=2034 解题思路:set的基本用法 #include<iostream> #include& ...
- 后缀数组 POJ 3974 Palindrome && URAL 1297 Palindrome
题目链接 题意:求给定的字符串的最长回文子串 分析:做法是构造一个新的字符串是原字符串+反转后的原字符串(这样方便求两边回文的后缀的最长前缀),即newS = S + '$' + revS,枚举回文串 ...
- ural 2071. Juice Cocktails
2071. Juice Cocktails Time limit: 1.0 secondMemory limit: 64 MB Once n Denchiks come to the bar and ...
- ural 2073. Log Files
2073. Log Files Time limit: 1.0 secondMemory limit: 64 MB Nikolay has decided to become the best pro ...
- ural 2070. Interesting Numbers
2070. Interesting Numbers Time limit: 2.0 secondMemory limit: 64 MB Nikolay and Asya investigate int ...
- ural 2069. Hard Rock
2069. Hard Rock Time limit: 1.0 secondMemory limit: 64 MB Ilya is a frontman of the most famous rock ...
- ural 2068. Game of Nuts
2068. Game of Nuts Time limit: 1.0 secondMemory limit: 64 MB The war for Westeros is still in proces ...
随机推荐
- 使用MFC读写Excel
_Application m_ExlApp; //组件服务器的各个classes _Workbook m_ExlBook; Workbooks m_ExlBooks; _W ...
- git 更换远程仓库地址
1. 更改软件仓库指向.在github改了用户名和仓库名称后,仓库地址也相应的发生的变化,这时候就需要更新本地仓库以指向新的远程仓库地址: $git remote set-url origin git ...
- MyEclipse Web Project导入Eclipse Dynamic Web Project,无法部署到tomcat问 题
做作业遇到一个小问题,将MyEclipse Web Project导入到Eclipse中开发.在部署到tomcat时,发现无法发布这个项目. 问题分析: MyEclipse Web Project被识 ...
- php的一些基本概念梳理
楼主是个刚参加工作的菜鸟,这几天刚开通博客园微博,想通过这个平台与大家共同学习与分享一些技术知识. 但是楼主犹豫的好久,不知道第一篇该写点什么.最后我决定先从php的一些基本概念开始,以便加深对各个概 ...
- Examples_08_08
aaarticlea/png;base64,iVBORw0KGgoAAAANSUhEUgAAARYAAAGsCAIAAACXfh8LAAAgAElEQVR4nO2db3AT193v903e8yIzbV
- sql server语句
一.基础1.说明:创建数据库CREATE DATABASE 数据库名2.说明:删除数据库drop database 数据库名3.说明:备份sql server--- 创建 备份数据的 deviceUS ...
- smokeping报错Can't locate RRDs.pm in @INC (@INC contains
安装完smokeping,执行debug语句: ./bin/smokeping --debug-daemon ,提示如下错误: Can't locate RRDs.pm in @INC (@INC c ...
- 关于Aspose对于Word操作的一些扩展及思考
Aspose.word Aspose.Words是一款先进的类库,通过它可以直接在各个应用程序中执行各种文档处理任务.Aspose.Words支持DOC,OOXML,RTF,HTML,OpenDocu ...
- JavaScript Arguments 实现可变参数的函数,以及函数的递归调用
//可变参数的函数 注:也可以使用对象作为参数来实现 function Max() { var temp = arguments[0] || 0; for (var i = 1; i < arg ...
- CSS中zoom:1的作用
兼容IE6.IE7.IE8浏览器,经常会遇到一些问题,可以使用zoom:1来解决,有如下作用:触发IE浏览器的haslayout解决ie下的浮动,margin重叠等一些问题.比如,本站使用DIV做一行 ...
