codeforces 192A Funky Numbers

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

As you very well know, this year's funkiest numbers are so called triangular numbers (that is, integers that are representable as 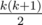, where k is some positive integer), and the coolest numbers are those that are representable as a sum of two triangular numbers.

A well-known hipster Andrew adores everything funky and cool but unfortunately, he isn't good at maths. Given number n, help him define whether this number can be represented by a sum of two triangular numbers (not necessarily different)!

Input

The first input line contains an integer n (1 ≤ n ≤ 109).

Output

Print "YES" (without the quotes), if n can be represented as a sum of two triangular numbers, otherwise print "NO" (without the quotes).

Examples

input

256

output

YES

input

512

output

NO

Note

In the first sample number .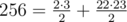

In the second sample number 512 can not be represented as a sum of two triangular numbers.

#include<cstdio>
#include<iostream>
#include<cmath>
#include<cstdlib>
#include<algorithm>
using namespace std;
#define f(x) (x)*(x+1)/2
int main()
{

    int i=,j=,n;
    bool flag=false;
    while(~scanf("%d",&n))
    {
        flag=false;
        for(i=;f(i)+f(j)<=n;i++)
        {
            for(j=i;f(i)+f(j)<=n;j++)
            {
                if(f(i)+f(j)==n)
                {
                    printf("YES\n");
                    flag=true;
                    break;
                }
            }
            if(flag)
                break;
            j=;
        }
        if(!flag)
            printf("NO\n");
    }
    return ;
}