PIE 阻断回溯——Cut

PIE（Prolog Inference Engine）通常是搜索所有的解。举个例子，

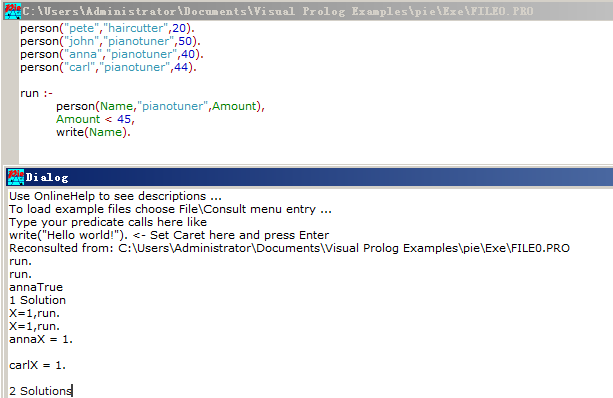
当然dialog窗口中一开始调用 run. 只会显示一个解（虽然事实上会得到两个解），在前面加上 X=1，就可以将两个解都显示出来。

有时候我们只需要得到一个解就行，此时如果让PIE算出所有的解，显然会浪费时间降低效率。这时我们就可以使用 cut 来解决这个问题。

假设有如下规则，rule

r1 :- a,b,c.

有三个 subgoal，分别是 a，b，c。PIE推断的时候依次计算a，b，c，当c失败时，可能会回溯b（如果b有回溯点的话），甚至会回溯到a。现在在这条rule中加上一个 cut （使用 ! 符号）

r1 :- a,b,!,c.

可以将!看作一个subgoal。现在在b和c直接有一个cut，这导致在c之前的所有 subgoal（这里是a 和 b）将不会被设置回溯点，对PIE来说，计算subgoal a 和 b 的第一个解已经足够了，不会再计算满足 a 和 b 的其他解。当然，PIE还是可以计算搜索满足c的很多个解。

Cut的作用

1）在一个rule中，位于 ! 之前的subgoal不会被设置回溯点。

2）在几个定义相同rule的规则中（定义一个rule可能会有多个从句clause），某一个rule中的 ! 会导致其他从句中不会被设置回溯点。

看一个实际的例子，还是上图中的那个例子，在run规则中加入一个cut，则只有一个解

run :-
         person(Name,"pianotuner",Amount),
         Amount < , !
         write(Name).

这是一个阻断其他subgoal被回溯的例子。下面再看一个其他从句被阻断的例子

cut会告诉PIE已经选择了一个正常的从句来计算推导，故而没有必要再选择其他从句来计算。例如，考虑如下代码，

r():- ! , a , b , c.
r():- ! , d.
r():- ! , c.
r(_):- write("This is a catchall clause.").

这里有四个从句定义了规则r。Prolog调用 r 并传入一个整形参数，假设调用的是 r(1)，Prolog搜索程序代码，以找到满足r(1)的解。考虑到对r(1)而言，可能有不止一个解，故Prolog在r(2)处设置一个回溯点，然后进入r(1)进行计算，进入r(1)后Prolog首先就看到!符号，这个cut会导致移除所有其他从句被设置回溯点的可能性，然后Prolog依次计算a，b，c，并且不会回溯到其他r从句中。注意到上面最后一个从句非常类似其他语言中的异常捕获，由于cut的作用也使得在进入r(1)进行计算后，Prolog不应该再调用异常捕获从句。

上面这组规则还可以写成如下形式，

r(X) :- X =  , ! , a , b , c.
r(X) :- X =  , ! , d.
r(X) :- X =  , ! , c.
r(_) :- write("This is a catchall clause.").

当然，前一种写法程序执行效率更高，并且可读性也更好。