POJ1988(Cube Stacking)--并查集

题目链接：http://poj.org/problem?id=1988

题意：有n个元素，开始每个元素各自在一个栈中，有两种操作，将含有元素x的栈放在含有y的栈的顶端，合并为一个栈。

第二种操作是询问含有x元素下面有多少个元素。

思路：

并查集，把每一堆看作一个栈，堆的下方看作栈顶。因为当我们知道栈中元素的总数，和某元素到“栈顶”的距离，

我们就能知道这个元素下面有多少元素。合并操作的时候，始终使用在下面栈的根来做合并之后的根，这样也就达到了栈中的根是栈中的“栈顶”元素的效果，我们只需在每个“栈顶”中记录该栈中的元素总数即可。然而我们还需要得知某元素到“栈顶”的距离，这样我们就需要记录每个元素到其父亲的距离，把它到根上所经过的距离加起来，即为它到“栈顶”的距离。这样我们就得出了结果。

 

这个图是在合并的时候的关键部分 

另外，在进行Find()操作时，有一句 under[x] += under[t[x].parent];这句话就是在递归寻找根结点时，计算出每个元素距离栈底（根）的距离。

 #include<iostream>
 #include<stdio.h>
 #include<cstring>
 #include<cmath>
 #include<vector>
 #include<stack>
 #include<map>
 #include<set>
 #include<list>
 #include<queue>
 #include<string>
 #include<algorithm>
 #include<iomanip>
 using namespace std;

 struct node
 {
     int parent;
     int date;
 };

 int * total;
 int * under;

 class DisJoinSet
 {
 protected:
     int n;

     node * tree;
 public:
     DisJoinSet(int n);
     ~DisJoinSet();
     void Init();
     int Find(int x);
     void Union(int x,int y);
 };

 DisJoinSet::DisJoinSet(int n)
 {
     this->n = n;
     tree = new node[n+];
     total = new int[n+];
     under = new int[n+];
     Init();
 }
 DisJoinSet::~DisJoinSet()
 {
     delete[] under;
     delete[] total;
     delete[] tree;
 }

 void DisJoinSet::Init()
 {
     for(int i = ;i  <= n ;i ++)
     {
         tree[i].date  = i;
         tree[i].parent = i;
         total[i] = ;
         under[i] = ;
     }
 }
 int DisJoinSet::Find(int x)
 {
     //int temp = tree[x].parent;
     if(x != tree[x].parent)
     {
         int par = Find(tree[x].parent);
         under[x] += under[tree[x].parent];//把父亲结点下面的个数加到自己头上
         tree[x].parent = par;
         return tree[x].parent;
     }
     else
     {
         return x;
     }
 }

 void DisJoinSet::Union(int x,int y)
 {
     int pa = Find(x);
     int pb = Find(y);
     if(pa == pb)return ;
     else
     {
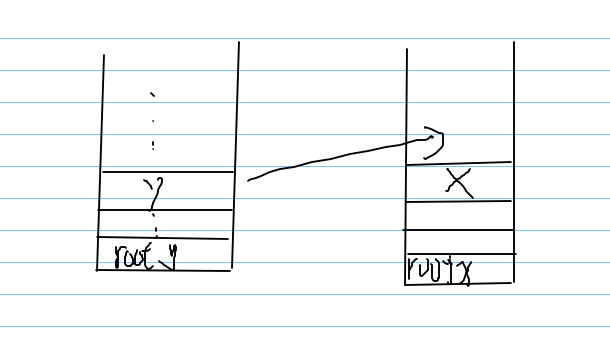
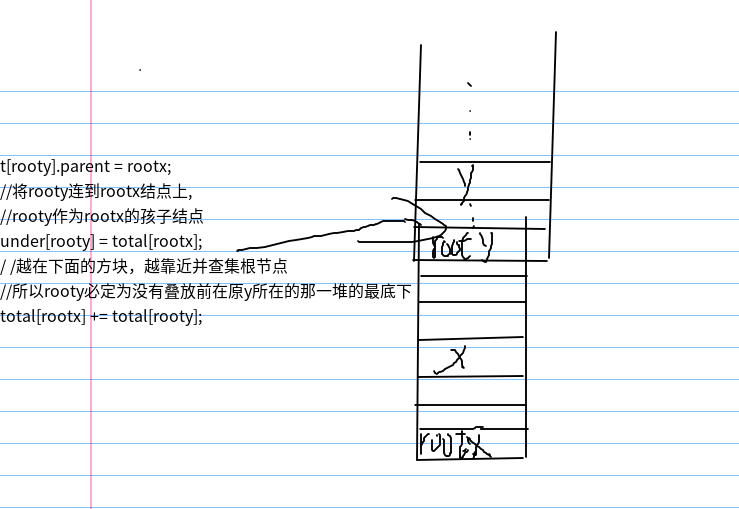
         tree[pa].parent = pb;//x的根变为y的根  即把x所在的堆放在y所在的堆上面
         under[pa] = total[pb];//pa下的数量即原来y所在栈里的元素total
         total[pb] += total[pa];//更新y的totoal
     }
 }

 int main()
 {
     int p;
     while(scanf("%d",&p) != EOF)
     {
         if(p == )break;
         DisJoinSet dis(p);
         char s1[];
         for(int i =  ;i < p ;i++)
         {

             int s2;
             int s3;
             scanf("%s",s1);
             if(s1[] == 'M')
             {
                 scanf("%d%d",&s2,&s3);
                 int pa = dis.Find(s2);
                 int pb = dis.Find(s3);
                 if(pa != pb)
                 {
                     dis.Union(s2,s3);
                 }
             }
             if(s1[] == 'C')
             {
                 scanf("%d",&s2);
                 dis.Find(s2);
                 cout<<under[s2]<<endl;
             }
         }
         dis.~DisJoinSet();
     }
     return ;
 }