SGI RB-tree深入理解

前言

在学习STL源码之前我也曾无数次想要弄懂红黑数的原理，奈何每次都被困难打退。说实话，红黑树是真的很难理解，需要不断沉淀才能慢慢体会其妙处。这两天看SGI的RB-tree实现，结合侯捷老师的《STL源码剖析》，终于将主要的源码看懂了，人生如此艰难！所以我写一篇文章，来记下理解的过程，可以加深印象，以后还可以迅速重温。注意，本文主要参考侯捷的《STL源码剖析》，图片也基本按照书上的原图画的。

RB-tree概述

RB-Tree是一种被广泛使用的平衡二叉树，也是SGI STL唯一实现的一种搜索树，作为关联性容器的底层机制之用。RB-tree是平衡二叉搜索树的一种，通过特定的操作来保持树的平衡，理解RB-tree之前，建议先理解二叉搜索树的原理，最好是能理解AVL树的原理。

RB-tree定义

所谓RB-tree不仅是一个二叉搜索树，而且必须满足以下规则：

1. 每个节点不是红色就是黑色。

2. 根节点为黑色。

3. 如果节点为红，其子节点必须为黑。

4. 任一节点至NULL（树尾端）的任何路径，所含之黑节点树必须相同。

根据规则4，新增节点必须为红；根据规则3，新增节点之父节点必须为黑。当新节点根据二叉搜索树的规则到达其插入点，却未能符合上述条件时，就必须调旋转树形和调整颜色。

插入节点

在RB-tree插入新节点，一共有四种不同的典型，下面将分别举例分析。如下图所示，在RB-tree分别插入 3,8,35,75，根据二叉树的规则，这四个新节点分别落脚点应该落在下图空心框位置，它们都破坏了RB-tree的规则，因此必须要调整树形，也就是旋转树形并改变节点颜色。注意，状况3和状况4和《STL源码剖析》侯捷讲的是不一样的，侯捷讲的是先选择后改变节点颜色。但我看源码实现只改变颜色。仔细分析其实侯捷讲的这种也没错，只是有些多余了，而且和源码不一致，会误导人，我觉得我这么分析更好。

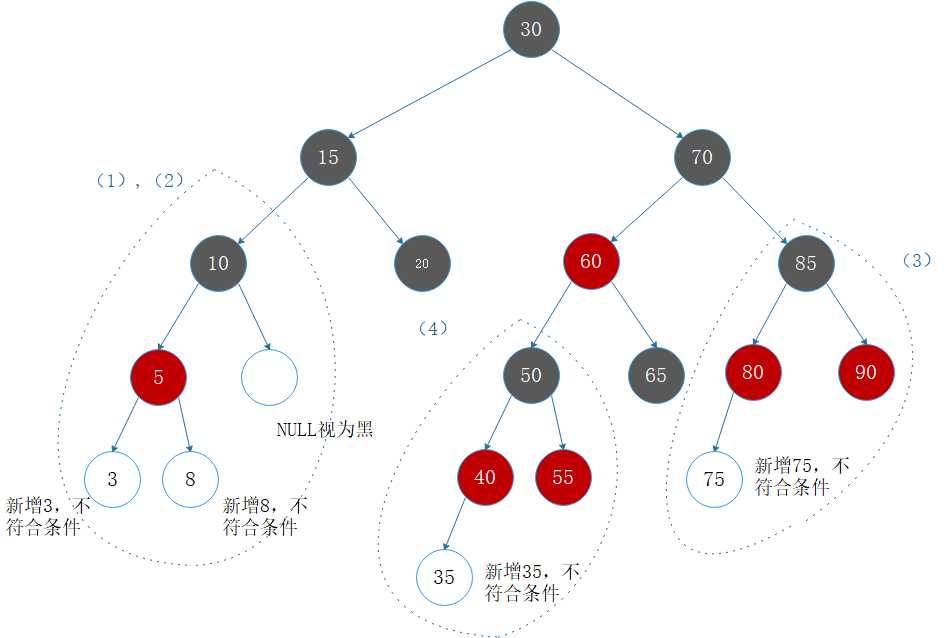
为方便讨论，先定义一些代名。假设新节点为X，其父节点为P，祖父节点为G，伯父节点（父节点之兄弟节点）为S，曾祖父节点为GG。根据二叉搜索树的规则，新节点X必为叶节点，根据红黑树规则4，X必为红。若P亦为红（这就违反了规则3，必须调整树形），则G必为黑（因为原为RB-tree，必须遵循规则3）。

状况1：S为黑且X为外侧插入。对此情况，先对P，G做一次单旋转，再更改P，G颜色，即可重新满足红黑树的规则3，如下图所示。注意，此时可能产生不平衡状态（高度相差1以上）。例如图中旋转后的3左右节点肯定为NULL，但空心框不为空且其左右节点不为NULL。这倒没关系，因为RB-tree的平衡性本来就比AVL-tree弱。然而RB-tree通常能够保持良好的平衡状态。是的，经验告诉我们，RB-tree的搜寻平均效率和AVL-tree几乎相等。

 状况2：S为黑且X为内侧插入。对此情况，先对P，X做一次单旋转，再更改P，X颜色，再将结果对G做一次单旋转，即可重新满足红黑树的规则3，如下图所示。

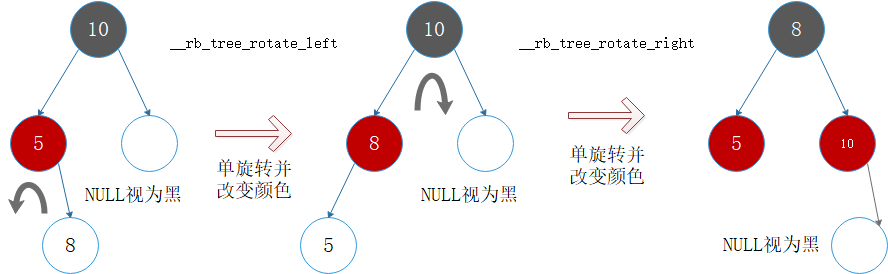
状况3：S为红且X为外侧插入。对此情况，改变P和S为黑，G为红，如果GG为黑，一切搞定，如下图所示。但如果GG为红，则问题比较大......见状况4。

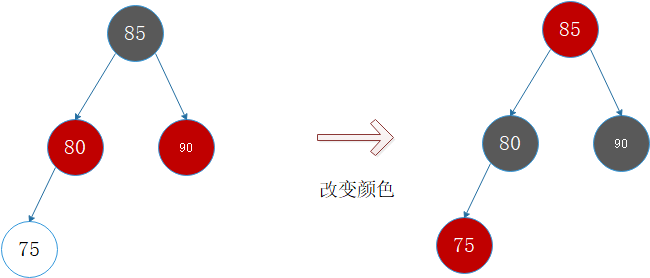
 状况4：S为红且X为外侧插入。对此情况，改变P和S为黑，G为红，此时GG亦为红，还得继续往上做，直到不再有父子连续为红的情况。

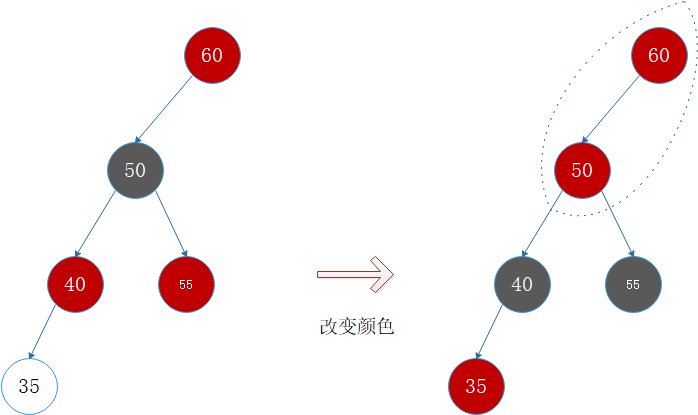
RB-tree节点设计

RB-tree的节点在二叉树的节点结构上增加红黑颜色属性，而且为了更好的进行插入和删除操作，增加指向父亲节点的指针。为了更大的弹性，STL红黑树的节点采用双层设计，STL红黑树的节点采用双层设计，base结构不依赖模板参数，带模板的节点结构继承base结构。从以下的源码中的 minimum() 和 maximum() 函数可以看出，RB-tree作为一个二叉搜索树，其极值是很容易找到的。

typedef bool __rb_tree_color_type;
const __rb_tree_color_type __rb_tree_red = false;    //红色为0
const __rb_tree_color_type __rb_tree_black = true;   //黑色为1

struct __rb_tree_node_base
{
  typedef __rb_tree_color_type color_type;
  typedef __rb_tree_node_base* base_ptr;

  color_type color;  //节点颜色，非红即黑
  base_ptr parent;   //RB树的许多操作必须知道父节点
  base_ptr left;     //指向左节点
  base_ptr right;    //指向右节点

  static base_ptr minimum(base_ptr x)
  {
    while (x->left != ) x = x->left;  //一直向左走，就会找到最小值
    return x;                          //这是二叉搜索树的特性
  }

  static base_ptr maximum(base_ptr x)
  {
    while (x->right != ) x = x->right;  //一直向右走，就会找到最大值
    return x;                            //这是二叉搜索树的特性
  }
};

//真正的节点定义，基类中不含模板参数
template <class Value>
struct __rb_tree_node : public __rb_tree_node_base
{
  typedef __rb_tree_node<Value>* link_type;
  Value value_field;  //节点值
};

RB-tree迭代器

要成功地将RB-tree实现为一个泛型容器，迭代器的设计是一个关键，首先要考虑它的型别（category），然后考虑它的前进（increment）、后退（decrement）、提领（dereference）、成员访问（member access）等操作。

为了更大的弹性，SGI将RB-tree迭代器实现为两层，这种设计理念和slist类似（slist学习后续补上）。下图（图片来自《STL源码剖析》）是双层节点结构和双层迭代器结构之间的关系，其中主要意义是：__rb_tree_node 继承自 __rb_tree_node_base，__rb_tree_iterator 继承自 __rb_tree_base_iterator。有了这样的认识，我们就可以将迭代器稍作转型，就可以解开RB-tree的所有奥秘，追踪其一切状态。从源代码可以看出，不论是RB-tree的节点还是迭代器，都是以struct完成，而struct的所有成员都是public，可被外界自由取用。

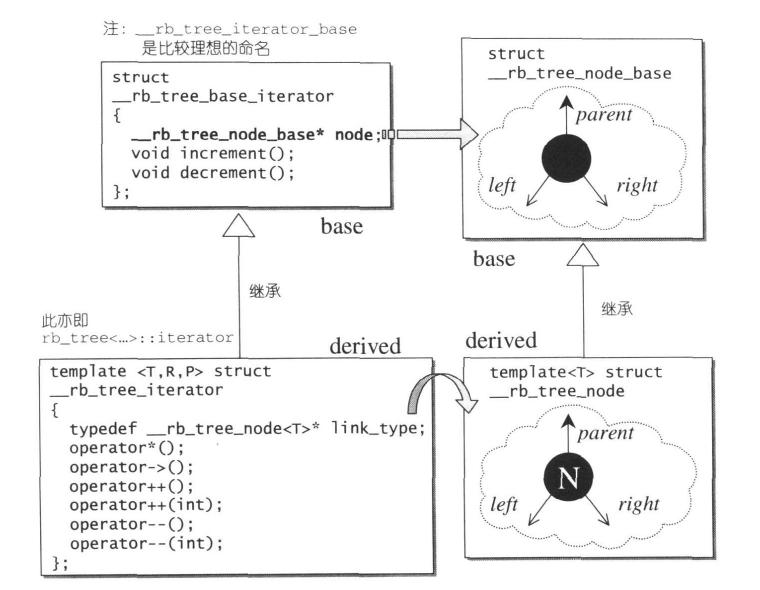
RB-tree迭代器属于双向迭代器，但不具备随机访问能力，其提领和成员访问操作比较特殊，有前进和后退操作。注意，RB-tree迭代器的前进操作 operator++() 调用了基层的 increment()，后退操作 operator--() 则调用了基层迭代器的 decrement()。前进或后退操作完全依据二叉搜索树的节点排序法则，再加上实现上的某些特殊技巧。至于特殊技巧主要与根节点有关。

//基层接迭代器
struct __rb_tree_base_iterator
{
  typedef __rb_tree_node_base::base_ptr base_ptr;
  typedef bidirectional_iterator_tag iterator_category;
  typedef ptrdiff_t difference_type;
  base_ptr node;  //它用来和容器之间产生一个连结关系

  //前进只用于operator++内，再无他出调用
  void increment()
  {
    if (node->right != ) {        //如果有右子节点，下面操作
      node = node->right;          //使node取得右子树最小值
      while (node->left != )
        node = node->left;
    }
    else {                         //没有右子节点
      base_ptr y = node->parent;   //取父节点
      while (node == y->right) {   //如果node是右子节点
        node = y;                  //继续上溯，直到不为右子节点为止
        y = y->parent;
      }
      if (node->right != y)        //若此时的右子节点不等于父亲节点
        node = y;                  //父亲节点即为答案，
    }
  }

  //前进只用于operator--内，再无他出调用
  void decrement()
  {
    if (node->color == __rb_tree_red &&  //如果是红且
        node->parent->parent == node)    //父节点的父节点等于自己
      node = node->right;                //右节点即为解答
      //以上情况发生于node为header时(即node为end())
      //header右子节点即mostright，指向整棵树max节点
    else if (node->left != ) {          //存在左子节点
      base_ptr y = node->left;           //去左子树最大值
      while (y->right != )
        y = y->right;
      node = y;
    }
    else {                              //左子节点不存在
      base_ptr y = node->parent;        //取父节点
      while (node == y->left) {         //如果node是左子节点
        node = y;                       //继续上溯，直到不为左子节点为止
        y = y->parent;
      }
      node = y;                         //此时y即为解答
    }
  }
};

//RB-tree正规迭代器
template <class Value, class Ref, class Ptr>
struct __rb_tree_iterator : public __rb_tree_base_iterator
{
  typedef Value value_type;
  typedef Ref reference;
  typedef Ptr pointer;
  typedef __rb_tree_iterator<Value, Value&, Value*>             iterator;
  typedef __rb_tree_iterator<Value, const Value&, const Value*> const_iterator;
  typedef __rb_tree_iterator<Value, Ref, Ptr>                   self;
  typedef __rb_tree_node<Value>* link_type;

  __rb_tree_iterator() {}
  __rb_tree_iterator(link_type x) { node = x; }
  __rb_tree_iterator(const iterator& it) { node = it.node; }

  reference operator*() const { return link_type(node)->value_field; }
#ifndef __SGI_STL_NO_ARROW_OPERATOR
  pointer operator->() const { return &(operator*()); }
#endif 

  self& operator++() { increment(); return *this; }
  self operator++(int) {
    self tmp = *this;
    increment();
    return tmp;
  }

  self& operator--() { decrement(); return *this; }
  self operator--(int) {
    self tmp = *this;
    decrement();
    return tmp;
  }
};

header实现技巧

树状结构的各种操作，最需要注意的就是边界情况的发生，也就是走到根节点时要有特殊的处理。为了简化处理，SGI特别为根节点再设计一个父节点，名为header，并令其初始状态如下图所示。

图左是RB-tree的初始化状态，图右是加入一个节点后的状态。接下来，每当插入新节点时，不但要按照RB-tree的规则来调整，并且维护header的正确性，使其父节点指向根节点，左子节点指向最小节点，右子节点指向最大节点。

RB-tree数据结构

下面是rb_tree的定义。其中定义专属的空间配置器，每次用来配置一个节点大小，KeyOfValue是获取key值得仿函数，Compare是用来比较节点大小的仿函数。还是其他的解析见代码注释，理解起来不难。

template <class Key, class Value, class KeyOfValue, class Compare,
          class Alloc = alloc>
class rb_tree {
protected:
  typedef void* void_pointer;
  typedef __rb_tree_node_base* base_ptr;
  typedef __rb_tree_node<Value> rb_tree_node;
  typedef simple_alloc<rb_tree_node, Alloc> rb_tree_node_allocator; //专属空间配置器
  typedef __rb_tree_color_type color_type;
public:
  //iterator定义在后面
  typedef Key key_type;
  typedef Value value_type;
  typedef value_type* pointer;
  typedef const value_type* const_pointer;
  typedef value_type& reference;
  typedef const value_type& const_reference;
  typedef rb_tree_node* link_type;
  typedef size_t size_type;
  typedef ptrdiff_t difference_type;
protected:
  link_type get_node() { return rb_tree_node_allocator::allocate(); }
  void put_node(link_type p) { rb_tree_node_allocator::deallocate(p); }

  link_type create_node(const value_type& x) {
    link_type tmp = get_node();        //配置空间
    __STL_TRY {
      construct(&tmp->value_field, x); //构造内容
    }
    __STL_UNWIND(put_node(tmp));
    return tmp;
  }

  link_type clone_node(link_type x) {  //复制一个节点(值和色)
    link_type tmp = create_node(x->value_field);
    tmp->color = x->color;
    tmp->left = ;
    tmp->right = ;
    return tmp;
  }

  void destroy_node(link_type p) {
    destroy(&p->value_field);  //释放内容
    put_node(p);               //释放内存
  }

protected:
  size_type node_count; //追踪记录树的大小(节点数量)
  link_type header;     //这是实现上的一个技巧
  Compare key_compare;  //节点间键值大小比较准则，应该是个function object

  //以下三个函数用来方便取得header的成员
  link_type& root() const { return (link_type&) header->parent; }
  link_type& leftmost() const { return (link_type&) header->left; }
  link_type& rightmost() const { return (link_type&) header->right; }

  //以下六个函数用来方便取得节点x的成员
  static link_type& left(link_type x) { return (link_type&)(x->left); }
  static link_type& right(link_type x) { return (link_type&)(x->right); }
  static link_type& parent(link_type x) { return (link_type&)(x->parent); }
  static reference value(link_type x) { return x->value_field; }
  static const Key& key(link_type x) { return KeyOfValue()(value(x)); }
  static color_type& color(link_type x) { return (color_type&)(x->color); }

  //以下六个函数用来方便取得节点x的成员
  static link_type& left(base_ptr x) { return (link_type&)(x->left); }
  static link_type& right(base_ptr x) { return (link_type&)(x->right); }
  static link_type& parent(base_ptr x) { return (link_type&)(x->parent); }
  static reference value(base_ptr x) { return ((link_type)x)->value_field; }
  static const Key& key(base_ptr x) { return KeyOfValue()(value(link_type(x))); }
  static color_type& color(base_ptr x) { return (color_type&)(link_type(x)->color); }

  static link_type minimum(link_type x) {
    return (link_type)  __rb_tree_node_base::minimum(x);
  }
  static link_type maximum(link_type x) {
    return (link_type) __rb_tree_node_base::maximum(x);
  }

public:
  typedef __rb_tree_iterator<value_type, reference, pointer> iterator;
  typedef __rb_tree_iterator<value_type, const_reference, const_pointer>
          const_iterator;

  typedef reverse_iterator<const_iterator> const_reverse_iterator;
  typedef reverse_iterator<iterator> reverse_iterator;

private:
  iterator __insert(base_ptr x, base_ptr y, const value_type& v);
  link_type __copy(link_type x, link_type p);
  void __erase(link_type x);
  void init() {
    header = get_node();           //产生一个节点空间
    color(header) = __rb_tree_red; //令header为红，用来区分header和
                                   //root, 在iterator.operator--
    root() = ;
    leftmost() = header;           //令header左子节点为自己
    rightmost() = header;          //令header右子节点为自己
  }
public:
  rb_tree(const Compare& comp = Compare())  //默认构造调init
    : node_count(), key_compare(comp) { init(); }

  rb_tree(const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& x)
    : node_count(), key_compare(x.key_compare)  //拷贝构造
  {
    header = get_node();
    color(header) = __rb_tree_red;
    if (x.root() == ) {  //x根节点为空，整个过程其实和init一样
      root() = ;
      leftmost() = header;
      rightmost() = header;
    }
    else { //存在x根节点
      __STL_TRY {
        root() = __copy(x.root(), header);  //调用全局复制函数
      }
      __STL_UNWIND(put_node(header));
      leftmost() = minimum(root());         //header左指针指向的最小值点
      rightmost() = maximum(root());        //header右指针指向的最大值点
    }
    node_count = x.node_count;
  }
  ~rb_tree() {
    clear();
    put_node(header);
  }
  rb_tree<Key, Value, KeyOfValue, Compare, Alloc>&
  operator=(const rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& x);

public:
                                // accessors:
  Compare key_comp() const { return key_compare; }
  iterator begin() { return leftmost(); }               //RB-tree起头为最左节点处
  const_iterator begin() const { return leftmost(); }   //RB-tree终点为header所指处
  iterator end() { return header; }
  const_iterator end() const { return header; }
  reverse_iterator rbegin() { return reverse_iterator(end()); }
  const_reverse_iterator rbegin() const {
    return const_reverse_iterator(end());
  }
  reverse_iterator rend() { return reverse_iterator(begin()); }
  const_reverse_iterator rend() const {
    return const_reverse_iterator(begin());
  }
  bool empty() const { return node_count == ; }
  size_type size() const { return node_count; }
  size_type max_size() const { return size_type(-); }

  void swap(rb_tree<Key, Value, KeyOfValue, Compare, Alloc>& t) {
    __STD::swap(header, t.header);
    __STD::swap(node_count, t.node_count);
    __STD::swap(key_compare, t.key_compare);
  }

public:
                                // insert/erase
  pair<iterator,bool> insert_unique(const value_type& x);
  iterator insert_equal(const value_type& x);

  iterator insert_unique(iterator position, const value_type& x);
  iterator insert_equal(iterator position, const value_type& x);

  template <class InputIterator>
  void insert_unique(InputIterator first, InputIterator last);
  template <class InputIterator>
  void insert_equal(InputIterator first, InputIterator last);

  void erase(iterator position);
  size_type erase(const key_type& x);
  void erase(iterator first, iterator last);
  void erase(const key_type* first, const key_type* last);
  void clear() {
    if (node_count != ) {
      __erase(root());      //释放所有节点
      leftmost() = header;
      root() = ;
      rightmost() = header;
      node_count = ;
    }
  }      

public:
                                // set operations:
  iterator find(const key_type& x);
  const_iterator find(const key_type& x) const;
  size_type count(const key_type& x) const;
  iterator lower_bound(const key_type& x);
  const_iterator lower_bound(const key_type& x) const;
  iterator upper_bound(const key_type& x);
  const_iterator upper_bound(const key_type& x) const;
  pair<iterator,iterator> equal_range(const key_type& x);
  pair<const_iterator, const_iterator> equal_range(const key_type& x) const;

public:
                                // Debugging.
  bool __rb_verify() const;
};

RB-tree元素操作

读源码过程中，发现真正的插入函数__insert(base_ptr x, base_ptr y, const value& v)的参数x几乎没什么用，对这个问题非常迷惑。后来查了一些资料，发现x是在调用一个insert重载函数时发挥作用。STL关联容器map/multimp，set/multiset，都是使用了红黑树的底层结构。insert有两个重载函数，一个insert(const Value&)，另一个是insert_unique(iterator， const Value&)，后者是带hint的插入。《C++标准程序库》中说道：若被安插元素位置恰好紧贴于提示位置之后，那么时间复杂度就会从“对数”变为“摊还常数”。当hint恰当时，可大大加快速度。

对于map和set，insert函数会调用rb-tree中的insert_unique版本，对于multimap和multiset，则调用rb-tree中的insert_equal版本。由于insert_equal较insert_unique简单一些，所以这里只分析insert_unique。

template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::
__insert(base_ptr x_, base_ptr y_, const Value& v) {
  //x_为新值插入点，y_为插入点父节点，参数v为新值
  link_type x = (link_type) x_;
  link_type y = (link_type) y_;
  link_type z;

  if (y == header || x !=  || key_compare(KeyOfValue()(v), key(y))) {
    //y为header或x!=0或v小于父节点
    z = create_node(v);         //产生一个新节点
    left(y) = z;                //also makes leftmost() = z when y == header
    if (y == header) {
      root() = z;
      rightmost() = z;
    }
    else if (y == leftmost())   //如果y为最左节点
      leftmost() = z;           //maintain leftmost() pointing to min node
  }
  else {
    z = create_node(v);         //产生一个新节点
    right(y) = z;               //令新节点称为y的右子节点
    if (y == rightmost())       //如果y为最右节点
      rightmost() = z;          //maintain rightmost() pointing to max node
  }
  parent(z) = y;
  left(z) = ;
  right(z) = ;
  __rb_tree_rebalance(z, header->parent);  //树调整
  ++node_count;
  return iterator(z);
}

template <class Key, class Value, class KeyOfValue, class Compare, class Alloc>
pair<typename rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::iterator, bool>
rb_tree<Key, Value, KeyOfValue, Compare, Alloc>::insert_unique(const Value& v)
{
  link_type y = header;
  link_type x = root();
  bool comp = true;
  while (x != ) {
    y = x;
    comp = key_compare(KeyOfValue()(v), key(x));
    x = comp ? left(x) : right(x);
  }
  iterator j = iterator(y);
  if (comp)
    if (j == begin())
      return pair<iterator,bool>(__insert(x, y, v), true);
    else
      --j;
  if (key_compare(key(j.node), KeyOfValue()(v)))
    return pair<iterator,bool>(__insert(x, y, v), true);
  return pair<iterator,bool>(j, false);
}

template <class Key, class Val, class KeyOfValue, class Compare, class Alloc>
typename rb_tree<Key, Val, KeyOfValue, Compare, Alloc>::iterator
rb_tree<Key, Val, KeyOfValue, Compare, Alloc>::insert_unique(iterator position,
                                                             const Val& v) {
  if (position.node == header->left) // begin()
    if (size() >  && key_compare(KeyOfValue()(v), key(position.node)))
      return __insert(position.node, position.node, v);
  // first argument just needs to be non-null
    else
      return insert_unique(v).first;
  else if (position.node == header) // end()
    if (key_compare(key(rightmost()), KeyOfValue()(v)))
      return __insert(, rightmost(), v);
    else
      return insert_unique(v).first;
  else {
    iterator before = position;
    --before;
    if (key_compare(key(before.node), KeyOfValue()(v))
        && key_compare(KeyOfValue()(v), key(position.node)))
      if (right(before.node) == )
        return __insert(, before.node, v);
      else
        return __insert(position.node, position.node, v);
    // first argument just needs to be non-null
    else
      return insert_unique(v).first;
  }
}

RB-tree旋转及改变颜色

inline void
__rb_tree_rotate_left(__rb_tree_node_base* x, __rb_tree_node_base*& root)
{
  __rb_tree_node_base* y = x->right;  //取x右节点
  x->right = y->left;                 //x右指针指向y左节点
  if (y->left !=)                    //y左节点存在
    y->left->parent = x;              //其父指针指向x，回马枪
  y->parent = x->parent;              //y父指针指向x父亲节点

  if (x == root)                      //当x为根节点时
    root = y;                         //根节点赋为y
  else if (x == x->parent->left)      //x为左子节点
    x->parent->left = y;              //x父节点左指针指向y
  else                                //x为右子节点
    x->parent->right = y;             //x父节点右指针指向y
  y->left = x;                        //y左指针指向x
  x->parent = y;                      //x父指针指向y，回马枪
}

//原理和左旋一样，只方向全部逆转，不再注解
inline void
__rb_tree_rotate_right(__rb_tree_node_base* x, __rb_tree_node_base*& root)
{
  __rb_tree_node_base* y = x->left;
  x->left = y->right;
  if (y->right != )
    y->right->parent = x;
  y->parent = x->parent;

  if (x == root)
    root = y;
  else if (x == x->parent->right)
    x->parent->right = y;
  else
    x->parent->left = y;
  y->right = x;
  x->parent = y;
}