python 拟合曲线并求参

需要对数据进行函数拟合，首先画一下二维散点图，目测一下大概的分布，

所谓正态分布，就是高斯分布，正态曲线是一种特殊的高斯曲线。

python的scipy.optimize包里的curve_fit函数来拟合曲线，当然还可以拟合很多类型的曲线。scipy.optimize提供了函数最小值(标量或多维)、曲线拟合和寻找等式的根的有用算法。

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit
import math
#单个高斯模型，如果曲线有多个波峰，可以分段拟合

def func(x, a,u, sig):
    return a*np.exp(-(x - u) ** 2 / (2 * sig ** 2)) / (sig * math.sqrt(2 * math.pi))
#混合高斯模型，多个高斯函数相加

def func3(x, a1, a2, a3, m1, m2, m3, s1, s2, s3):
    return a1 * np.exp(-((x - m1) / s1) ** 2) + a2 * np.exp(-((x - m2) / s2) ** 2) + a3 * np.exp(-((x - m3) / s3) ** 2)

#正弦函数拟合

#def fmax(x,a,b,c):
#    return a*np.sin(x*np.pi/6+b)+c
#fita,fitb=optimize.curve_fit(fmax,x,ymax,[1,1,1])
#非线性最小二乘法拟合
#def func(x, a, b,c):
#    return a*np.sqrt(x)*(b*np.square(x)+c)
#用3次多项式拟合，可推广到n次多项式，数学上可以证明，任意函数都可以表示为多项式形式
#f1 = np.polyfit(x, y, 3)
#p1 = np.poly1d(f1)
#yvals = p1(x)  #拟合y值
#也可使用yvals=np.polyval(f1, x)

拟合，并对参数进行限制，bounds里面代表参数上下限，p0是初始范围，默认是[1,1,1]

x=np.arange(1,206,1)

num = []<-自己的y值

numhunt = []<-自己的y值

y = np.array(num)

yhunt = np.array(numhunt)

popt, pcov = curve_fit(func3, x, y)

popthunt, pcovhunt = curve_fit(func, x, yhunt,p0=[2,2,2]) 

ahunt = popthunt[0]
uhunt = popthunt[1]
sighunt = popthunt[2]

a1 = popt[0]
u1 = popt[1]
sig1 = popt[2]
a2 = popt[3]
u2 = popt[4]
sig2 = popt[5]
a3 = popt[6]
u3 = popt[7]
sig3 = popt[8]

yvals = func3(x,a1,u1,sig1,a2,u2,sig2,a3,u3,sig3) #拟合y值
yhuntvals = func(x,ahunt,uhunt,sighunt) #拟合y值

print(u'系数ahunt:', ahunt)
print(u'系数uhunt:', uhunt)
print(u'系数sighunt:', sighunt)

#绘图
plot1 = plt.plot(x, y, 's',label='insect original values')
plot2 = plt.plot(x, yvals, 'r',label='insect polyfit values')
plot3 = plt.plot(x, yhunt, 's',label='predator original values')
plot4 = plt.plot(x, yhuntvals, 'g',label='predator polyfit values')

plt.xlabel('date')
plt.ylabel('Nightly catches log10(N+1)')
plt.legend(loc=4) #指定legend的位置右下角
plt.title('insect/predator')
plt.show()

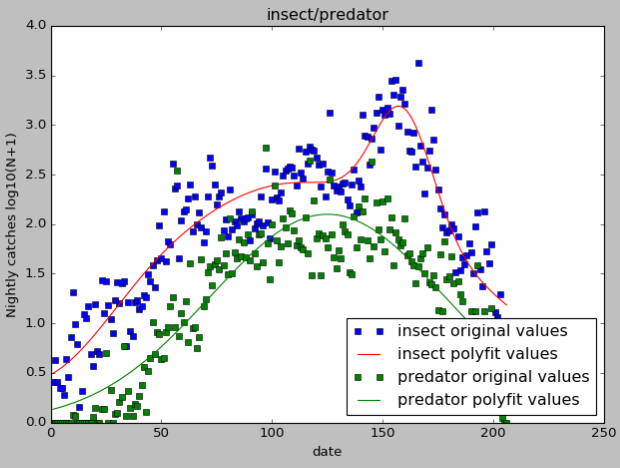
下图是单个和多个高斯拟合图像

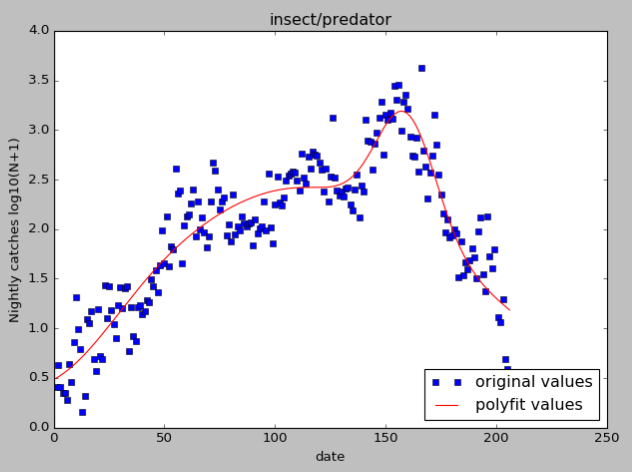
下图是多项式拟合图像

图例的位置可以自定义设置

lower left
upper center
lower right
center
upper left
center left
upper right
lower center
best
center right
right