AtCoder Beginner Contest 144 题解

传送门

$cf$ 自闭了，打 $abc$ 散散心

A - 9x9

...这个有什么好讲的吗，题目看懂就会做了

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
inline int read()
{
    int x=,f=; char ch=getchar();
    while(ch<''||ch>'') { if(ch=='-') f=-; ch=getchar(); }
    while(ch>=''&&ch<='') { x=(x<<)+(x<<)+(ch^); ch=getchar(); }
    return x*f;
}
int a,b;
int main()
{
    a=read(),b=read();
    if(a>||b>||a<||b<) { printf("-1\n"); return ; }
    printf("%d\n",a*b);
    return ;
}

A

B - 81

预处理一下哪些数可以被表示然后查表即可

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
inline int read()
{
    int x=,f=; char ch=getchar();
    while(ch<''||ch>'') { if(ch=='-') f=-; ch=getchar(); }
    while(ch>=''&&ch<='') { x=(x<<)+(x<<)+(ch^); ch=getchar(); }
    return x*f;
}
const int N=;
bool vis[N];
int main()
{
    for(int i=;i<=;i++)
        for(int j=;j<=;j++) vis[i*j]=;
    int a=read();
    if(vis[a]) printf("Yes\n");
    else printf("No\n");
    return ;
}

B

C - Walk on Multiplication Table

根号枚举一下因数，设因数为 $x$ ，那么看看走到 $(x,n/x)$ 是不是比较短的路径即可

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
inline ll read()
{
    ll x=,f=; char ch=getchar();
    while(ch<''||ch>'') { if(ch=='-') f=-; ch=getchar(); }
    while(ch>=''&&ch<='') { x=(x<<)+(x<<)+(ch^); ch=getchar(); }
    return x*f;
}
ll n,ans;
int main()
{
    n=read(); int t=sqrt(n);
    ans=n-;
    for(int i=;i<=t;i++)
    {
        if(n%i) continue;
        ans=min(ans,n/i+i-);
    }
    printf("%lld\n",ans);
    return ;
}

C

D - Water Bottle

对我这个数学不好的人来说很不友好啊...

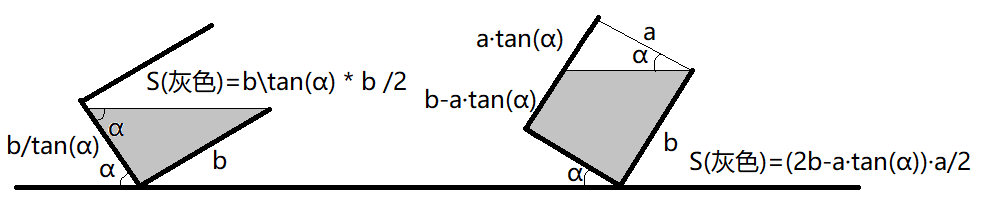
显然二分一下倾斜角看看水是否会倒出来

首先可以把 $x$ 除以 $a$ ，然后就变成平面的问题

然后要特判一下内部是梯形还是三角形就做完了，要注意一下细节，别和我一样把精度设到 $1e-18$ 或者 $-1e18$ ，$\text{2333333}$

放张图比较好理解吧：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
typedef long double ldb;
inline int read()
{
    int x=,f=; char ch=getchar();
    while(ch<''||ch>'') { if(ch=='-') f=-; ch=getchar(); }
    while(ch>=''&&ch<='') { x=(x<<)+(x<<)+(ch^); ch=getchar(); }
    return x*f;
}
const ldb pi=acos(-1.0),eps=1e-;
ldb a,b,x,ans;
inline bool check(ldb alp)
{
    if(a*tan(alp)>=b)
    {
        ldb y=b/tan(alp);
        return y*b/<=x;
    }
    ldb t=b-a*tan(alp);
    return (t+b)*a/<=x;
}
int main()
{
    cin>>a>>b>>x;
    x/=a;
    ldb L=eps,R=pi/-eps;
    while(fabsl(R-L)>eps)
    {
        ldb mid=(L+R)/;
        if(check(mid)) R=mid,ans=mid;
        else L=mid;
    }
    printf("%.12Lf\n",ans/pi*);
    return ;
}

D

E - Gluttony

首先容易想到最大的 $A$ 和最小的 $F$ 匹配，次大的和次小的匹配...这样匹配下去

然后考虑如何减一些 $A$ ，显然可以二分答案，那么 $check$ 长这样：

inline bool check(ll p)//二分的答案p
{
    ll now=K;
    for(int i=;i<=n;i++)
    {
        // af<=p , a<=p/f
        if(p/F[i]>=A[i]) continue;
        ll t=A[i]-p/F[i];
        if(t>now) return ;
        now-=t;
    }
    return ;
}

分析完代码发现，为了最优一定要 $A$ 从小到大对应匹配 $F$ 从大到小，一种证明大概是这样的：

首先可以发现，对于二分的答案 $p$ ，它需要的 $K$ 为 $\sum_{i=1}^{n}max(A_i-\left \lfloor \frac{p}{F_i}\right \rfloor,0)$

那么式子相当于 $\sum_{i=1}^{n}A_i-\sum_{i=1}^{n}\left \lfloor \frac{p}{F_i}\right \rfloor+\sum_{i=1}^{n}[A_i<\left \lfloor \frac{p}{F_i}\right \rfloor](\left \lfloor \frac{p}{F_i}\right \rfloor-A_i)$

发现如果某种匹配能让最后一项求和尽量小，那么即为最优的

然后问题就变成了给长度为 $n$ 的序列 $A,B$ ，求一种匹配使 $\sum_{i=1}^{n}[A_i<B_i](B_i-A_i)$ 最小

首先对于最大的 $B_x$ ，如果 $A_i,A_j$ 都大于 $B_x$ ，那么 $i,j$ 选那个没影响，如果 $A_i<B<A_j$ 显然要让 $A_j$ 去和 $B_x$ 匹配

因为如果让 $A_i$ 和 $B_x$ 匹配，首先产生的代价一定大于 $A_i$ 和 $B_y,y\neq x$ 匹配的代价，然后 $A_j$ 不管和谁匹配代价都为 $0$，那么综合一下还是要让 $A_j$ 去匹配 $B_x$

如果 $A_i<A_j<B$ ，那么如果 $A_i$ 和 $B_x$ 匹配并且 $A_j$ 和 $B_y$ 匹配，如果 $A_j<B_y$ 那么交换 $i,j$ 对答案没影响

但是如果 $A_j>B_y$ ，自己写一下式子会发现代价大于等于 $A_j$ 和 $B_x$ 匹配，$A_i$ 和 $B_y$ 匹配的代价（这里要再分 $B_y$ 和 $A_i$ 之间的关系讨论）

所以综上，$A$ 中最大的和 $B$ 中最大的匹配，次大的和次大的匹配，这样下去一定不会劣于其他方案

回到原来的问题，因为 $F$ 变成了分母，所以要 $F$ 最小的和 $A$ 最大的匹配

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
inline ll read()
{
    ll x=,f=; char ch=getchar();
    while(ch<''||ch>'') { if(ch=='-') f=-; ch=getchar(); }
    while(ch>=''&&ch<='') { x=(x<<)+(x<<)+(ch^); ch=getchar(); }
    return x*f;
}
const int N=2e5+;
const ll INF=1e12;
ll n,m,A[N],F[N];
inline bool check(ll p)
{
    ll now=m;
    for(int i=;i<=n;i++)
    {
        // af<=p , a<=p/f
        if(p/F[i]>=A[i]) continue;
        ll t=A[i]-p/F[i];
        if(t>now) return ;
        now-=t;
    }
    return ;
}
int main()
{
    n=read(),m=read();
    for(int i=;i<=n;i++) A[i]=read();
    for(int i=;i<=n;i++) F[i]=read();
    sort(A+,A+n+); sort(F+,F+n+);
    reverse(F+,F+n+);
    ll L=,R=INF,ans=;
    while(L<=R)
    {
        ll mid=L+R>>;
        if(check(mid)) R=mid-,ans=mid;
        else L=mid+;
    }
    printf("%lld\n",ans);
    return ;
}

E

F - Fork in the Road

一开始显然会考虑枚举断边然后 $dp$ 一下算代价

设 $f[x]$ 表示从 $x$ 出发最终到达 $n$ 的期望步数，那么转移显然

但是枚举断边复杂度为 $m$，总复杂度为 $m(n+m)$ ，不太行

考虑枚举点，对于某个点 $u$ ，它有若干的出边 $(u,v_i)$

考虑断掉哪条从 $u$ 出发的边是最优的，显然是 $f[v_i]$ 最大的那个，所以只要考虑断最大的那个即可

那么枚举点的复杂度为 $n$ ，总复杂度为 $n(n+m)$，记得如果某个点没法走到 $n$ ，那么期望步数为 $INF$

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<vector>
using namespace std;
typedef long long ll;
typedef double db;
inline int read()
{
    int x=,f=; char ch=getchar();
    while(ch<''||ch>'') { if(ch=='-') f=-; ch=getchar(); }
    while(ch>=''&&ch<='') { x=(x<<)+(x<<)+(ch^); ch=getchar(); }
    return x*f;
}
const int N=,INF=1e9;
int n,m,a[N*N],b[N*N];
vector <int> V[N];
db f[N],ans;
inline db calc(int p)
{
    for(int i=;i<=n;i++) f[i]=;
    f[n]=;
    for(int i=n-;i>=;i--)
    {
        int len=V[i].size();
        if(p==i&&len==) { f[i]=INF; continue; }
        db t=1.0/(len-(p==i)),mx=;
        for(int j=;j<len;j++)
        {
            int v=V[i][j]; mx=max(mx,(f[v]+)*t);
            f[i]+=(f[v]+)*t;
        }
        if(p==i) f[i]-=mx;
    }
    return f[];
}
int main()
{
    n=read(),m=read();
    for(int i=;i<=m;i++)
    {
        a[i]=read(),b[i]=read();
        V[a[i]].push_back(b[i]);
    }
    ans=calc();
    for(int i=;i<=n;i++)
        ans=min(ans,calc(i));
    printf("%.9lf\n",ans);
    return ;
}

F