NOIP原题 斗地主（20190804）

题目描述

牛牛最近迷上了一种叫斗地主的扑克游戏。斗地主是一种使用黑桃、红心、梅花、方片的A到K加上大小王的共54张牌来进行的扑克牌游戏。在斗地主中，牌的大小关 系根据牌的数码表示如下：3<4<5<6<7<8<9<10<J<Q<K<A<2<小王<大王，而花色并不对牌的大小产生影响。每一局游戏中，一副手牌由 n 张牌组成。游戏者每次可以根据规定的牌型进行出牌，首先打光自己的手牌一方取得游戏的胜利。

现在，牛牛只想知道，对于自己的若干组手牌，分别最少需要多少次出牌可以将它们打光。请你帮他解决这个问题。

需要注意的是，本题中游戏者每次可以出手的牌型与一般的斗地主相似而略有不同。具体规则如下：

输入格式

第一行包含用空格隔开的2个正整数 T,nT,n ，表示手牌的组数以及每组手牌的张数。

接下来 TT 组数据，每组数据 nn 行，每行一个非负整数对 a_i,b_iai​,bi​ ，表示一张牌，其中 a_iai​ 表示牌的数码， b_ibi​表示牌的花色，中间用空格隔开。特别的，我们用 11 来表示数码 AA， 1111 表示数码JJ， 1212 表示数码QQ， 1313 表示数码 KK；黑桃、红心、梅花、方片分别用 1-41−4 来表示；小王的表示方法为 0101 ，大王的表示方法为 0202 。

输出格式

共 TT 行，每行一个整数，表示打光第 ii 组手牌的最少次数。

输入输出样例

输入 #1

8
7 4
8 4
9 1
10 4
11 1
5 1
1 4
1 1

输出 #1

  3

输入 #2

    1 17

12 3
4 3
2 3
5 4
10 2
3 3
12 2
0 1
1 3
10 1
6 2
12 1
11 3
5 2
12 4
2 2
7 2

输出 #2

  6

说明/提示

样例1说明

共有11组手牌，包含8张牌：方片77，方片88，黑桃99，方片1010，黑桃JJ，黑桃55，方片AA以及黑桃AA。可以通过打单顺子（方片77，方片88，黑桃99，方片1010，黑桃JJ），单张牌（黑桃55）以及对子牌（黑桃AA以及方片AA）在33次内打光。

对于不同的测试点， 我们约定手牌组数TT与张数nn的规模如下：

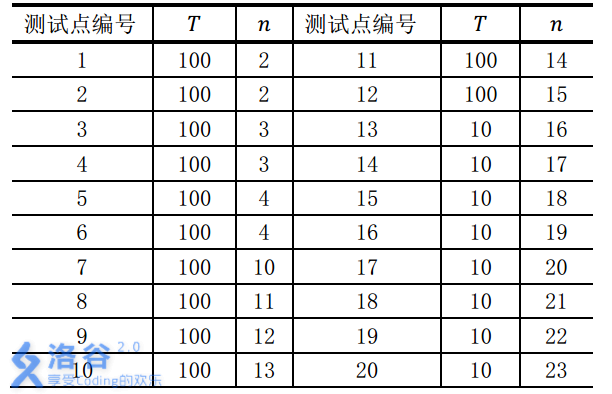
数据保证：所有的手牌都是随机生成的。

一句话概括题目意思就是斗地主，有多种出牌方式，求最快出完要几步。

思路：

这题只记得当时去郑州时老师没怎么细说，就说打了搜索搞了八九十分，好像还是当年的第三题，不由得感叹，要是现在的NOIP还是这样该多好。。。。。

昨天在机房就听到zwjdd和shymm感叹出法的不常规，洛谷题解里也都是“我斗地主会玩，这题不会打”的感叹。。。。，感觉要不是打过一遍也要GG。。。

这题感觉就是搜索一个一个找，感觉和原来那个麻将好像。。。。

• 无论怎么搞，顺子都有利于我们打出5或以上的牌，一下子能少掉好多，所以顺子的优先级最高，其余的东西以后一个一个搞就好了。
• 然后可以适当的剪下枝，毕竟全是for 也怪吓人的。。。
• 如果当前的出牌数已经超过了当前最优的ans，剪了（最优性剪枝）
• 其他还有一些神奇的剪枝，如先出牌数多的，后出牌数少的，感觉这样能过，就没加。。。。
• 顺子要暴力找，不要搞什么幺蛾子。。。。就像3,4,5,6,7,6,7,8,9,10，如果用什么方法去处理有可能就变成了了最长的，这样就剩下了两张牌，但如果出两个顺子，就比上一种方案优秀，所以要暴力，也许是有什么方法可以预处理出来，但我还是太菜了
• 贪心打散牌，先出四带二，再出三带一，以此类推，这个仅可用与NOIP原题

     下面是搜索顺序：

• 要注意一个地方两个王不一样，不能当一对，只有火箭可以。，然后就是暴搜，感觉就要注意一下细节。

 #include<iostream>
 using namespace std;
 int T,n,ans,sum[];
 void dfs(int x)//x为出牌次数
 {
     if (x>=ans)
     return;
     //顺子
     int k=;//单顺子
     for (int i=;i<=;i++)//注意2和大小王不能考虑
     {
         if(sum[i]==) k=;//顺子断了
         else
         {
             k++;//顺子长度增加
             if(k>=)//单顺子达到五张
             {
                 for(int j=i;j>=i-k+;j--)
                 sum[j]--;//出牌
                 dfs(x+);//继续搜
                 for(int j=i;j>=i-k+;j--)
                 sum[j]++;//回溯
             }
         }
     }
     k=;//双顺子
     for(int i=;i<=;i++)
     {
         if(sum[i]<=) k=;
         else
         {
             k++;
             if(k>=)//双顺子达到三组
             {
                 for(int j=i;j>=i-k+;j--)
                 sum[j]-=;//出牌
                 dfs(x+);
                 for(int j=i;j>=i-k+;j--)
                 sum[j]+=;//回溯
             }
         }
     }
     k=;//三顺子    //以下同理
     for(int i=;i<=;i++)
     {
         if(sum[i]<=) k=;
         else
         {
             k++;
             if(k>=)//三顺子达到两组
             {
                 for(int j=i;j>=i-k+;j--) sum[j]-=;
                 dfs(x+);
                 for(int j=i;j>=i-k+;j--) sum[j]+=;
             }
         }
     }
     //带牌
     for(int i=;i<=;i++)//枚举有3张或4张的牌（这样才能带牌）
     {
         if(sum[i]<=)
         {
             if(sum[i]<=)
             continue;//三张以下（不含三张）不能带牌
             sum[i]-=;//出掉用来带别人的牌
             for(int j=;j<=;j++)//带单张
             {
                 if(sum[j]<=)
                 continue;//没有牌怎么带？？
                 sum[j]--;//出掉被带的单张
                 dfs(x+);
                 sum[j]++;//回溯
             }
             for(int j=;j<=;j++)//带一对
             {
                 if(sum[j]<=)
                 continue;//没有一对怎么带？
                 sum[j]-=;//出掉被带的一对
                 dfs(x+);
                 sum[j]+=;//回溯
             }
             sum[i]+=;//回溯
         }
         else//大于3可以4带别的也可以3带别的
         {
             sum[i]-=;//先用3张带别的
             for(int j=;j<=;j++) //带单张  //以下原理同上
             {
                 if(sum[j]<=)
                 continue;
                 sum[j]--;
                 dfs(x+);
                 sum[j]++;
             }
             for(int j=;j<=;j++) //带一对
             {
                 if(sum[j]<=)
                 continue;
                 sum[j]-=;
                 dfs(x+);
                 sum[j]+=;
             }
             sum[i]+=;

             sum[i]-=; //再用4张带别的
             for(int j=;j<=;j++) //带2个单张
             {
                 if(sum[j]<=)
                 continue;//自己不能带自己喽
                 sum[j]--;//出被带的第一张单张牌
                 for (int k=;k<=;k++)//找第二张单张
                 {
                     if(sum[k]<=)
                      continue;
                     sum[k]--;//出被带的第二张单张牌
                     dfs(x+);
                     sum[k]++;//回溯
                 }
                 sum[j]++;//回溯
             }
             for(int j=;j<=;j++)//带2个对儿
             {
                 if(sum[j]<=)
                 continue;
                 sum[j]-=;//出被带的第一对牌
                 for(int k=;k<=;k++)
                 {
                     if(sum[k]<=)
                     continue;
                     sum[k]-=;//出被带的第二对牌
                     dfs(x+);
                     sum[k]+=;//回溯
                 }
                 sum[j]+=;//回溯
             }
             sum[i]+=;//回溯
         }
     }
     //把剩下的牌出完
     for(int i=;i<=;i++)
     {
         if(sum[i])
         {
                 x++;
         }
     }
     ans=min(ans,x);
 }
 int main()
 {
     scanf("%d%d",&T,&n);
     while(T--)
     {
         ans=<<;//搞大一点
         int x,y;
         memset(sum,,sizeof sum);//多次询问，记得清零
         for(int i=;i<=n;i++)
         {
             scanf("%d%d",&x,&y);
             if (x==)
             {
                 sum[]++;//把两张王存在一起（但是带牌的时候注意不要做对儿）
             }
             else
             if(x==)
             {
                 sum[]++;//由于A的牌值大所以往后放
             }
             else sum[x]++;//其他牌存在相应位置
         }
         dfs();//开始暴搜
         printf("%d\n",ans);
     }
 }

然后就可以把这道NOIP的简单题拿满啦！！！！！

然后，洛谷就有了对这题数据不服的一群大佬搞了这题（传送门）

然后去交了一发，就出事了。。。。。

能卡成这样，还是有些惊喜的。。。。。

由此可见：

• NOIP数据水的可怕----陈彦儒老师最后一天原话
• 用心出题目，用脚造数据--------zymdalao听完后的感叹

对于增强版，他主要就把贪心给卡了！！

对于原题像

4  4  4  8   8   8  K   K  K

会出三次三张牌的，然而可以这样出   4 4 4 8 8和  K K K 8这样就只要两步。

不用贪心，还能用啥？然后去看了看题解，发现了是DP，方程式还不是一般的多（蒟蒻表示推不出来）！！！！然后就在一对DP中发现了还有用贪心的（还是对的！！）

• 同样还是贪心打散牌，这也是不超时的原因。对于上面的贪心就会存在一些问题，增强后要考虑拆牌，王，也算是单排，可以当对子出。
• 拆牌（重点）： 什么时候可以拆呢？

1. 被四带的时候不能拆，这样可能会多出一次。
2. 在单牌和对牌很多时，三张和炸弹不可以拆，会多打，可能多很多次。
3. 反过来，单牌和对牌不是很多时，不就可以拆了吗？当单牌和对牌比三张和炸弹少时，就可以拆了。。。
4. 证明（没什么用）：这时不拆会没得带，例如单牌只能单出，如果把三张拆成一单一对，让其余和炸弹一起走，就会少一步
5. 举个栗子：  3 3 3   +7    and   9 9 9    and  5 5 5 5   ----->3  3  3  +9  9  and    5 5 5 5+9+7

原来       3步                                            后来     2步

四张是一样的。

愉快的代码环节（因为尝试新的打法，所以和原题的打法不太一样）

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 using namespace std;
 int n,t,ans;
 int pai[];//存牌
 int san_pai();
 void feiji(int step);
 void shunzi(int step);
 void liandui(int step);
 void chupai(int step) {      //开始出牌
     if(step>=ans)
     return ;   //最优性剪枝
     int tmp=san_pai();      //打散牌
     ans=min(tmp+step,ans); //更新最优解
     feiji(step);  //飞机
     shunzi(step); //顺子
     liandui(step);//连对
 }
 void feiji(int step)//出飞机
 {
     int l,end;
     for(int st=;st<=;++st) //枚举连续牌起始点
     {
         l=;
         while(pai[st+l]>=)
         l++;//找出最大长度
         for(int j=l;j>=;--j)
         {//枚举出牌长度
             end=st+j-;
             for(int k=st;k<=end;k++)
             pai[k]-=;//出飞机
             chupai(step+);//继续出牌
             for(int k=st;k<=end;k++)
             pai[k]+=;//搜索回溯
         }
     }
     return;
 }
 void liandui(int step)
 {//连对
     int l,end;
     for(int st=;st<=;++st)
     {//枚举连续牌起始点
         l=;
         while(pai[st+l]>=)l++;//找出最大长度
         for(int j=l;j>=;--j) {//枚举出牌长度
             end=st+j-;
             for(int k=st;k<=end;k++)
             pai[k]-=;//出连对
             chupai(step+);//继续出牌
             for(int k=st;k<=end;k++)
             pai[k]+=;//搜索回溯
         }
     }
     return;
 }
 void shunzi(int step) //顺子
 {
     int l,end;
     for(int st=;st<=;++st)
     {//枚举连续牌起始点
         l=;
         while(pai[st+l]>=)
         l++;//找出最大长度
         for(int j=l;j>=;--j)
         {
             end=st+j-;
             for(int k=st;k<=end;k++)
             pai[k]-=;//出顺子
             chupai(step+);//继续出牌
             for(int k=st;k<=end;k++)
             pai[k]+=;//搜索回溯
         }
     }
     return;
 }
 int san_pai() {//贪心打散牌
     int zs[],num=;
     memset(zs,,sizeof(zs));
     bool wangzha=false;
     if(pai[]==)
     wangzha=true;//是否有王炸
     zs[]+=pai[];            //王算单牌
     for(int i=;i<=;++i)zs[pai[i]]++;//统计个数
     /******  暴力出奇迹 , N!过样例  ******/
     while(!zs[]&&zs[]==&&zs[]==&&zs[]>)
     zs[]-=,zs[]--,zs[]--,num+=;//神特判
     //把一个炸拆成3张和单牌,再出一组四带二单和三带一
     while(!zs[]&&zs[]==&&zs[]==&&zs[]>)
     zs[]-=,zs[]--,zs[]--,num+=;//神特判
     //把一组三张拆成一对和一单,再出一组四带二单和三带二
     if(zs[]+zs[]>zs[]+zs[])//三四张的比单牌和对牌多,拆着打
         while(zs[]&&zs[]&&zs[])
         zs[]--,zs[]--,zs[]++,zs[]--,num++;//拆三张,4带两对余一单
     if(zs[]+zs[]>zs[]+zs[])//还多继续拆
         while(zs[]&&zs[]&&zs[])
         zs[]--,zs[]--,zs[]++,zs[]--,num++;//拆三张,4带两单余一对
     while(zs[]&&zs[]>)
     zs[]--,zs[]-=,num++;//四带两单
     while(zs[]&&zs[]>)
     zs[]--,zs[]-=,num++;//四带两对
     while(zs[]&&zs[]  )
     zs[]-- ,zs[]--,num++;//对看成两单再四带
     if(zs[]%==&&zs[]+zs[]<=)                //三张的太多了拆三张
         while(zs[]>)
         zs[]-=,num+=;//把一组三张拆成单和对,再出三带一和三带二
     while(zs[]&&zs[]  )
     zs[]-- ,zs[]--,num++;//三带一
     while(zs[]&&zs[]  )
     zs[]-- ,zs[]--,num++;//三带二
     //还剩三张和炸,组合出
     while(zs[]>&&zs[])
     zs[]--,zs[]-=,num+=;//把一个炸拆成一对和两单,再出三带二和四带两单
     while(zs[]>&&zs[])
     zs[]--,zs[]-=,num+=;//把一个炸拆成两对,再出两组三带一对
     while(zs[]>)
     zs[]-=,num+=;                //同上,把一组三张拆成单和对,再出三带一和三带二
     while(zs[]>)zs[]-=,num++;                //把一个炸拆成两对,再出一组四带两对
     if(wangzha&&zs[]>=)//有王炸并且没被带跑
         return num+zs[]+zs[]+zs[]+zs[]-;//双王一块出
     else
         return num+zs[]+zs[]+zs[]+zs[];//出剩余的牌,返回答案
 }
 int main()
 {
     cin>>t>>n;
     int a,b;
     while(t--)
     {
         ans=<<;
         memset(pai,,sizeof(pai));
         for(int i=; i<=n; ++i)
         {
             cin>>a>>b;
             if(a==)
             pai[]++;    //14代表A
             else
             if(a==)
             {
                 pai[]++;//1代表王
             }
             else
             pai[a]++;
         }
         chupai();
         printf("%d\n",ans);
     }
 }

最后预祝BK201    AK   IOI，还有希望shymm早日攒够350块钱，可以随时去这里水一下