金字塔卷积：Pyramidal Convolution

论文地址：https://arxiv.org/pdf/2006.11538.pdf

github：https://github.com/iduta/pyconv

作者认为，当前CNN主要存在两个不足：（1）实际的感受野不足；（2）在下采样中，很多的细节信息会丢失。

从图中可以看出，有的物体尺寸较大（建筑、沙发），有的物体尺寸较小（行人，书本）。这种尺寸的变化是标准卷积级经捕获的。为此，作者提出了金字塔卷积（Pyramid Convolution, PyConv），包含不同尺度的卷积核，可以提取多尺度信息，在多个任务上均取得了较好的性能

PyConv 的示意如图所示，直观来看，就是从上往下卷积核的大小依次减小，同时，在通道维度上，通道的数目依次增加。最后将得到的 feature map 拼接起来。

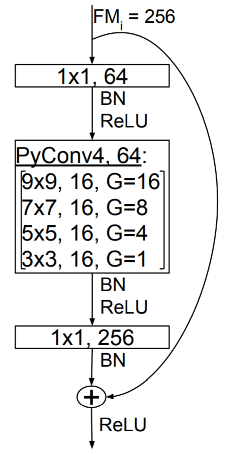
在图像分类任务中的 PyConv 示意所图所示，首先是9X9的卷积，16个卷积核，分为16组，因此生成16X16=256个 feature map；然后是7X7的卷积，16个卷积核，分为8组，因此生成16X8=128个 feature map；接着是5X5的卷积，16个卷积核，分为4组，因此生成16X4=64个 feature map；最后是3X3的卷积，16个卷积核，只有1组，因此生成16X1=16个 feature map。然后，会用1X1的卷积来使输出的维度都为 256。

备汪：关于分组卷积，网上有一个比较形象的图示。对于普通卷积，如果输入的 feature map 尺寸为CHW， 卷积核的数量为N，每个卷积核的尺寸为CxKxK，那么输出的 feature map 尺寸为 CHN，总的参数量为：NxCxKxK 。

如果进行分组卷积，假定要分成 G 组，每组输入的 feature map 数量为 \(\frac{C}{G}\)，每组输出的 feature map 数量为 \(\frac{N}{G}\)，每个卷积核的尺寸为\(\frac{C}{G}\times K\times K\), 每组的卷积核数量为 \(\frac{N}{G}\)，卷积核只与同组的输入进行卷积，则总的参数量为 \(N\times \frac{C}{G} \times K \times K\)，则总的参数量减少为以前的 \(\frac{1}{G}\)。

当分组数量等于输入map数量，输出map数量也等于输入map的数量，即 G=N=C，每个卷积核尺寸为\(1\times K \times K\)时，就成了 Depthwise convolution。

金字塔卷积 PyConv，通过集成不同尺度的卷积核，提升了多个视觉任务的性能，同时，该模块是一种“即插即用”的模块，可以较好的嵌入不同的网络架构中。