Java——排序算法

java排序从大的分类来看，可以分为内排序和外排序：其中，在排序过程中只使用了内存的排序称为内排序；内存和外存结合使用的排序成为外排序。

下面讲的都是内排序。

内排序在细分可以这样分：

1、选择排序：直接选择排序，堆排序

2、交换排序：冒泡排序，快速排序

3、插入排序：直接插入排序，二分插入排序，希尔排序

4、归并排序

5、基数排序

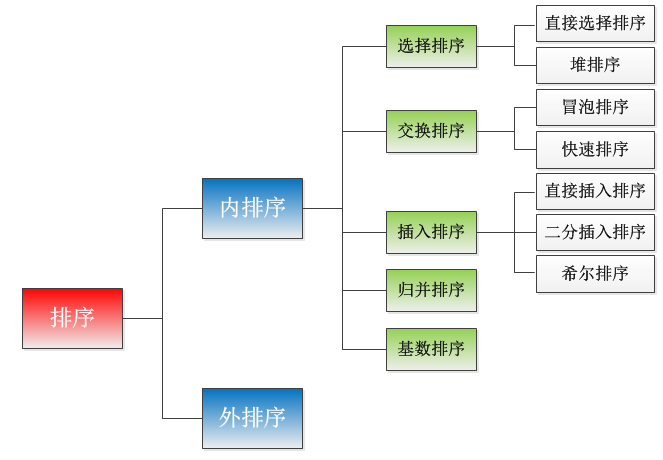
是不是觉得这样分类，文字的看着不形象，我也画了一张分类图：

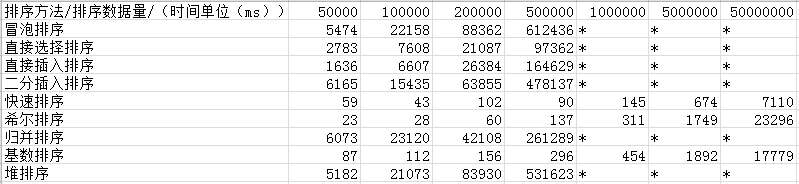
通过测试，我的测试数据（后面数据量大了，有的排序时间太长，我就用*代替了）：

通过测试数据来看，不同排序适用于不同的场景，快速排序也不一定是最快的，在数据量比较小的时候，希尔排序反而更快，只是在不断增加数据量的时候，快速排序比较快也很明显。同时，排序也不能只看排序的速度，还需要看它的空间复杂度，即对内存空间利用的要求。例如，快排、归并、堆排序这三者，通过随机数产生数组，它们的时间复杂度可以说是基本一样的，但是当n比较大的时候，你会发现归并排序会比其他两个慢。

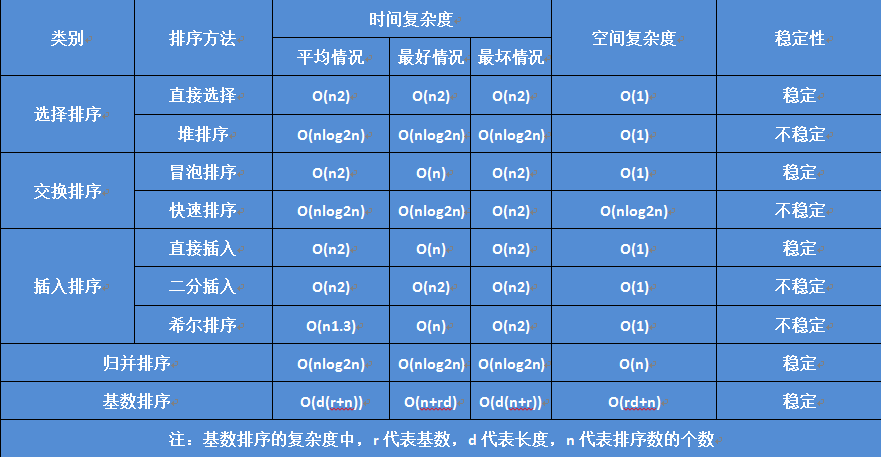
各种排序的时间复杂度、空间复杂度和稳定性，同样图形比较形象：

稳定性:
　  1、稳定：冒泡排序、插入排序、归并排序和基数排序
　  2、 不稳定：选择排序、快速排序、希尔排序、堆排序
平均时间复杂度
　　1、O(n^2):直接插入排序，简单选择排序，冒泡排序。
        2、在数据量特别大的时候，冒泡排序基本是最慢的。
　　3、在数据规模较小时（9W内），直接插入排序，简单选择排序差不多。当数据较大时，冒泡排序算法的时间代价最高。性能为O(n^2)的算法基本
上是相邻元素进行比较，基本上都是稳定的。
　　1、O(nlogn):快速排序，归并排序，希尔排序，堆排序。
　　2、其中，快排是最好的， 其次是归并和希尔，但数据量特别大的时候，归并排序很容易出现内存溢出的错误，如普通机器n>1000万时。
空间复杂度
         1、O(1):冒泡排序、直接插入排序、二分插入排序、希尔排序、直接选择排序、堆排序
         2、 O(n):归并排序
         3、 O(nlog2n):快速排序
         4、O(rd+n）:基数排序
排序算法的选择
　　1、数据规模较小
  　 （1）待排序列基本序的情况下，可以选择直接插入排序；
  　 （2）对稳定性不作要求宜用简单选择排序，对稳定性有要求宜用插入或冒泡
　　2、数据规模不是很大
　   （1）完全可以用内存空间，序列杂乱无序，对稳定性没有要求，快速排序，此时要付出log（N）的额外空间。
　   （2）序列本身可能有序，对稳定性有要求，空间允许下，宜用归并排序
　　 3、数据规模很大
        （1）对稳定性有求，则可考虑归并排序。
        （2）对稳定性没要求，可以用快速排序。
　　4、数组初始基本有序的时候，宜用直接插入排序，否则，可以用希尔排序。

下面是实现源码：

1. package sort;
2. /**
3. * Package: sort
4. *
5. * File: JavaSorts.java
6. *
7. * Copyright @ 2015 Corpration Name
8. *
9. */
10. public class JavaSorts {
11. /**
12. * 希尔排序
13. * @param array
14. */
15. public static void ShellSort(int[] array){
16. int d = array.length;
17. do {
18. d /= 2;   //设置增量,通过设置增量来进行分组，分组后，每一组内采用直接插入排序
19. OneShell(array, d);//一个增量对应一趟希尔排序
20. } while (d > 1);
21. }
22. /**
23. * 一趟希尔排序
24. * @param array
25. * @param d
26. */
27. public static void OneShell(int[] array,int d){
28. for (int i = 0; i < array.length - d; i++) {
29. int temp = array[i+d]; //array[i+d]的拷贝，每一次插入操作所以插入的值
30. if (array[i] > array[i + d]) {
31. int j = i;
32. //此时分组为：j,j+d,j+2d,j+3d····,组内采用直接插入排序
33. while(j >= 0 && array[j] > temp){
34. array[j + d] = array[j];    //使用while循环寻找temp能够插入的位置，从右往左寻找，大于temp的往后移动
35. j -= d;
36. }
37. array[j + d] = temp;   //插入数据
38. }
39. }
40. }
41. /**
42. * 快速排序
43. * @param array
44. * @param l
45. * @param r
46. */
47. public static void QuickSort(int[] array,int l,int r){
48. if (l < r) {
49. int i = l,j = r,temp = array[l];
50. while(i < j){
51. while(i < j && array[j] > temp){
52. j--;         //从右边开始寻找比temp小的数
53. }
54. if(i < j){
55. array[i++] = array[j]; //找到后，将这个数赋值到i位置上,然后i+1,因为下一轮寻找比temp大的数，从i+1位置开始
56. }
57. while(i < j && array[i] < temp){
58. i++;          //从左边寻找比temp大的数
59. }
60. if(i < j){
61. array[j--] = array[i]; //找到后，将这个数赋值到j位置上，然后j-1,因为下一轮寻找比temp小的数从j-1位置开始
62. }
63. }
64. array[i] = temp;  //此时比temp小的数都移动到左边，比temp大的数都移动到了右边，最后将temp赋值到中间位置
65. QuickSort(array, l, i - 1); //对temp左边的数进行递归
66. QuickSort(array, i + 1, r); //对temp右边的数进行递归
67. }
68. }
69. /**
70. * 堆排序
71. * @param array
72. */
73. public static void HeapSort(int[] array){
74. for (int i = 0; i < array.length; i++) {
75. BuildMaxHeap(array, array.length - 1 - i);
76. Swap(array, 0, array.length - 1 - i);
77. }
78. }
79. /**
80. * 创建最大堆
81. * @param array
82. * @param lastOneIndex
83. */
84. public static void BuildMaxHeap(int[] array,int lastOneIndex){
85. for (int i = (lastOneIndex - 1)/2; i >= 0; i--) {
86. int k = i;
87. while(2*k + 1 <= lastOneIndex){
88. int bigIndex = 2*k + 1;   //bigIndex用于记录一个节点树中最大数的索引
89. if (bigIndex < lastOneIndex) {  //满足这个条件，说明堆中有array[2*k+2]这个节点
90. if (array[bigIndex] < array[bigIndex + 1]) {
91. bigIndex++;      //若满足这个条件，说明k节点下的右子节点大于左子结点，因而bigIndex加1
92. }
93. }
94. if (array[k] < array[bigIndex]) {
95. Swap(array, bigIndex, k); //若k节点小于它其中一个子节点，则与这个子节点交换值
96. k = bigIndex;  //交换完值后，此时k节点下面的bigIndex节点可能不满足堆的性质，所以赋值给k,重新进入下一轮while循环
97. }else {
98. break;//若k节点满足堆的性质，则直接跳出循环
99. }
100. }
101. }
102. }
103. /**
104. * 交换array中array[a]、array[b]
105. * @param array
106. * @param a
107. * @param b
108. */
109. public static void Swap(int[] array,int a,int b){
110. if (a < array.length && b < array.length) {
111. int temp = array[a];
112. array[a] = array[b];
113. array[b] = temp;
114. }
115. }
116. /**
117. * 直接插入排序
118. * @param array
119. */
120. public static void DirectInsertSort(int[] array){
121. for (int i = 0; i < array.length - 1; i++) {
122. int temp = array[i + 1];
123. if (array[i] > array[i + 1]) {
124. int j = i;
125. while(j >= 0 && array[j] > temp){
126. array[j + 1] = array[j];
127. j--;
128. }
129. array[j + 1] = temp;
130. }
131. }
132. }
133. /**
134. * 二分插入排序
135. * @param array
136. */
137. public static void BinaryInsertSort(int[] array){
138. for (int i = 0; i < array.length - 1; i++) {
139. int temp = array[i + 1];  //需要插入的数
140. if(array[i] > array[i + 1]){
141. int l = 0;   //有序队列中左边标识
142. int r = i;   //有序队列中右边标识
143. while(l < r){
144. int mid = (l + r) / 2; //永远指向l->r中间的那个值，中间值与temp(需要插入的值)比较
145. if (array[mid] > temp) {
146. r--;              //通过while循环，二分折半搜索temp应该插入的位置
147. }else {
148. l++;
149. }
150. }
151. //运行到这里，l==r,即是temp应该插入的位置是array[l](或者array[r])
152. for (int j = i + 1; j > l; j--) {
153. array[j] = array[j - 1];  //将l -> i的数都往后移动一位
154. }
155. array[l] = temp;  //将temp插入到l位置
156. }
157. }
158. }
159. /**
160. * 直接选择排序
161. * @param array
162. */
163. public static void DirectSelectSort(int[] array){
164. for (int i = 0; i < array.length - 1; i++) {
165. int min = array[i];
166. for (int j = i + 1; j < array.length; j++) {
167. if (array[j] < min) {
168. min = array[j];
169. array[j] = array[i];
170. array[i] = min;
171. }
172. }
173. }
174. }
175. /**
176. * 冒泡排序
177. * @param array
178. */
179. public static void BubbleSort(int[] array){
180. int temp = 0;
181. for (int i = 0; i < array.length; i++) {
182. for (int j = 0; j < array.length - 1; j++) {
183. if (array[j] > array[j+1]) {
184. temp = array[j];
185. array[j] = array[j+1];
186. array[j+1] = temp;
187. }
188. }
189. }
190. }
191. /**
192. * 归并排序
193. * @param array
194. */
195. public static void MergeSort(int[] array){
196. int left = 0;
197. int right = array.length - 1;
198. MergeSortRecursive(array, left, right);
199. }
200. /**
201. * 归并排序的递归方法
202. * @param array
203. * @param left
204. * @param right
205. */
206. public static void MergeSortRecursive(int[] array,int left,int right){
207. if (left >= right) {
208. return;  //递归的停止判断，没有这个判断会报StackOverflowError
209. }
210. int mid = (left + right)/2;
211. MergeSortRecursive(array, left, mid);
212. MergeSortRecursive(array, mid+1, right);
213. Merge(array, left, mid, right);
214. }
215. /**
216. * 归并排序中合并方法
217. * @param array
218. * @param left
219. * @param mid
220. * @param right
221. */
222. public static void Merge(int[] array,int left,int mid,int right){
223. int r_left = mid + 1; //需要合并数组中右边数组第一个数索引
224. int[] tempArray = new int[array.length];//一个临时数组，用于合并时暂时存储
225. int newIndex = left;   //临时数组索引
226. int tempLeft = left;   //合并完了以后，用于复制数组的索引
227. while(left <= mid && r_left <= right){   //将部分的数放入到临时数组中
228. if (array[left] < array[r_left]) {
229. tempArray[newIndex++] = array[left++];
230. }else {
231. tempArray[newIndex++] = array[r_left++];
232. }
233. }
234. while (left <= mid) {
235. tempArray[newIndex++] = array[left++];  //将左边还剩余的数放入临时数组(若需要合并的左边还剩余数)
236. }
237. while(r_left <= right){
238. tempArray[newIndex++] = array[r_left++];//将右边还剩余的数放入临时数组(若需要和并的右边还剩余数)
239. }
240. while(tempLeft <= right){
241. array[tempLeft] = tempArray[tempLeft++];  //将临时数组复制到array
242. }
243. }
244. /**
245. * 基数排序
246. * @param array
247. */
248. public static void RadixSort(int[] array){
249. int bits = FindMaxBit(array);  //得到数组中最大的那个数的位数
250. for (int i = 0; i < bits; i++) {
251. OneBitSort(array, i+1);  //一位基数的排序
252. }
253. }
254. /**
255. * 一位基数的排序
256. * @param array
257. * @param bit
258. */
259. public static void OneBitSort(int[] array,int bit){
260. int[] tempArray = new int[array.length];
261. int index = 0;
262. int tempIndex = 0;
263. for (int i = 0; i < 10; i++) {
264. for (int j = 0; j < array.length; j++) {
265. if (FindBitNum(array[j], bit) == i) {
266. tempArray[index++] = array[j];
267. }
268. }
269. }
270. while(tempIndex < array.length){
271. array[tempIndex] = tempArray[tempIndex++]; //复制数组
272. }
273. }
274. /**
275. * 得到某个数某一位的数(例如：num=1234,n=2,FindBitNum(1234,2)=3)
276. * @param num
277. * @param n
278. * @return
279. */
280. public static int FindBitNum(int num,int n){
281. int key1 = (int)Math.pow(10, n);
282. int key2 = (int)Math.pow(10, n-1);
283. num %= key1;
284. num /= key2;
285. return num;
286. }
287. /**
288. * 得到一个数组中最大数的位数
289. * @param array
290. * @return
291. */
292. public static int FindMaxBit(int[] array){
293. if (array == null || array.length ==0) {
294. return 0;
295. }
296. int max = array[0];
297. for (int i = 1; i < array.length; i++) {
298. if (array[i] > max) {
299. max = array[i];
300. }
301. }
302. int bit = 0;
303. while(max / 10 != 0 || max % 10 != 0){
304. max /= 10;
305. bit++;
306. }
307. return bit;
308. }
309. public static void main(String[] args) {
310. System.out.println("冒泡排序："+SortThreads.getBubbleSortTime());
311. System.out.println("直接选择排序："+SortThreads.getDirSelectSortTime());
312. System.out.println("直接插入排序："+SortThreads.getDirInsertSortTime());
313. System.out.println("二分插入排序："+SortThreads.getBinaryInsertSortTime());
314. System.out.println("快速排序："+SortThreads.getQuickSortTime());
315. System.out.println("希尔排序："+SortThreads.getShellSortTime());
316. System.out.println("归并排序："+SortThreads.getMergeSortTime());
317. System.out.println("基数排序："+SortThreads.getRadixSortTime());
318. System.out.println("堆排序："+SortThreads.getHeapSortTime());
319. }
320. }

对于这些排序算法，我对它们的排序速度比较感兴趣，所以自己也测试了一下，数组是通过随机数产生的，我测的时候每一个数是不大于4位数，即不大于10000。

ProduceRandomNum.java产生随机数的数组：

1. package sort;
2. import java.util.Random;
3. /**
4. * Package: sort
5. *
6. * File: SortRunnable.java
7. *
8. * Copyright @ 2015 Corpration Name
9. *
10. */
11. public class ProduceRandomNum{
12. public synchronized static int[] RandomArray(int num,int n){
13. Random random = new Random();
14. int[] array = new int[num];
15. for (int i = 0; i < array.length; i++) {
16. array[i] = random.nextInt((int)Math.pow(10, n));
17. }
18. return array;
19. }
20. }

SortThreads.java测试排序的时间的方法，封装都一个类中，这个类我一直想把它写成多线程的方式（即是将这些排序一起运行），但是后面没有找到一个好的方法，所以后面就用了这种最笨的方法，有好办法的大神一定要指出来。

1. package sort;
2. /**
3. * Package: sort
4. *
5. * File: SortThreads.java
6. *
7. * Copyright @ 2015 Corpration Name
8. *
9. */
10. public class SortThreads {
11. private static final int arrayNum = 500000;
12. private static final int bit = 4;
13. public static long getBubbleSortTime(){
14. long oldTime = System.currentTimeMillis();
15. JavaSorts.BubbleSort(ProduceRandomNum.RandomArray(arrayNum, bit));
16. long newTime = System.currentTimeMillis();
17. return newTime - oldTime;
18. }
19. public static long getQuickSortTime(){
20. int[] array = ProduceRandomNum.RandomArray(arrayNum, bit);
21. long oldTime = System.currentTimeMillis();
22. JavaSorts.QuickSort(array, 0, array.length - 1);
23. long newTime = System.currentTimeMillis();
24. return newTime - oldTime;
25. }
26. public static long getDirSelectSortTime(){
27. long oldTime = System.currentTimeMillis();
28. JavaSorts.DirectSelectSort(ProduceRandomNum.RandomArray(arrayNum, bit));
29. long newTime = System.currentTimeMillis();
30. return newTime - oldTime;
31. }
32. public static long getDirInsertSortTime(){
33. long oldTime = System.currentTimeMillis();
34. JavaSorts.DirectInsertSort(ProduceRandomNum.RandomArray(arrayNum, bit));
35. long newTime = System.currentTimeMillis();
36. return newTime - oldTime;
37. }
38. public static long getBinaryInsertSortTime(){
39. long oldTime = System.currentTimeMillis();
40. JavaSorts.BinaryInsertSort(ProduceRandomNum.RandomArray(arrayNum, bit));
41. long newTime = System.currentTimeMillis();
42. return newTime - oldTime;
43. }
44. public static long getShellSortTime(){
45. long oldTime = System.currentTimeMillis();
46. JavaSorts.ShellSort(ProduceRandomNum.RandomArray(arrayNum, bit));
47. long newTime = System.currentTimeMillis();
48. return newTime - oldTime;
49. }
50. public static long getMergeSortTime(){
51. long oldTime = System.currentTimeMillis();
52. JavaSorts.MergeSort(ProduceRandomNum.RandomArray(arrayNum, bit));
53. long newTime = System.currentTimeMillis();
54. return newTime - oldTime;
55. }
56. public static long getRadixSortTime(){
57. long oldTime = System.currentTimeMillis();
58. JavaSorts.RadixSort(ProduceRandomNum.RandomArray(arrayNum, bit));
59. long newTime = System.currentTimeMillis();
60. return newTime - oldTime;
61. }
62. public static long getHeapSortTime(){
63. long oldTime = System.currentTimeMillis();
64. JavaSorts.HeapSort(ProduceRandomNum.RandomArray(arrayNum, bit));
65. long newTime = System.currentTimeMillis();
66. return newTime - oldTime;
67. }
68. }

转载：https://blog.csdn.net/u014039577/article/details/49667643