回归（Regression）

生活中的很多事物之间是相互影响的，如商品的质量跟用户的满意度密切相关。而回归分析是要分析两个事物间的因果关系，即哪一个是自变量和因变量，以及自变量和因变量之间的关系；回归有着较多的实际应用场景，如分析天气和空气中跟物质含量跟PM2.5浓度的关系，在分析出这一关系后，即可以用来预测未来某一时刻的PM2.5;如在无人车中，分析无人车红外线感测值、各个方向的视觉图等与方向盘角度之间的关系；

回归案例分析

分析神奇宝贝自身各个属性（也称作特征）跟进化后CP（Combat Power）值之间的关系；神奇宝贝是一个对象，我们可用通过这个对象的各个属性来对其进行描述。神奇宝贝的各种属性有：进化前的CP值、物种、生命值、体重、高度；

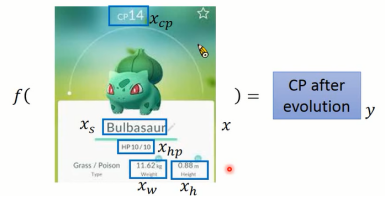
图1-1 神奇宝贝CP值预测

模型选择

我们需要用一个函数来表示神奇宝贝各个属性和进化后CP值的关系，但函数有千千万万，该如何选择？可以选择一个的线性函数来尝试，由于不知道那些属性跟最终的变量有真正关系，因此可以先只用一个可能有关系的变量进行尝试；最后的函数形式如（1）所示

数据收集

在确定模型的结构后，需要确定模型的参数w,b;而模型参数是要从数据集中来拟合出来。由于模型的结构为（1），因此模型的输入为进化前的CP值，输出为进化后的CP值，数据集。为了方便直观查看变量间的关系，往往需要对数据进行可视化

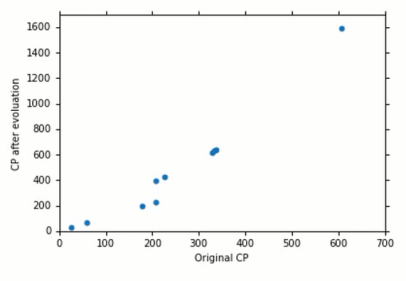
图1-2 进化前后CP值数据集

函数评估

我们最终的目的是要求解出（1）中的参数w,b;但w,b的取值是无限的，而哪一个取值才是最好的呢？损失函数（Loss Function）可以用来评估w,b取值的好坏。我们希望的是w,b能够使输出的跟尽可能的相近，因此损失函数可以定义为

参数优化

在确定好损失函数后，我们希望的是w，b能够使L(w,b)最小化，表明实际输出值和最接近。最佳的w，b用w*,b*来表示即

我们可以枚举所有的（w，b）来确定（w*,b*），只是这样太过麻烦甚至无法实现。因此需要有其他方法。当然也可以通过解线性方程来进行求解，而另外一种更加通用的解法就是梯度下降（Gradient Descent）。使用梯度下降的前提是L(w,b)为连续可微的！

w,b参数的更新形式为（4），

w，b的更新就是减去对应的偏导数；其中为学习率，控制着w，b的收敛速度；

泛化测试（Generalization Testing）

虽然在训练集上的，误差值已经优化的最小；但是，我们更关心的是训练出来后整个模型的泛化能力，即在测试集上对模型的预测误差进行测试；有时候我们的模型在训练集上已经训练到最好，但在测试集上却表现的很糟糕，这种现象称作“过拟合”。

模型迭代

在模型选择时，我们只是考虑最为简单的线性模型。因此，可以增加整个模型的复杂程度，例如可能增加二次式使模型可以表示曲线

在确定新的模型结构后，就可进行参数优化、泛化测试；虽然增加模型的复杂度，能够使模型在训练集上的误差减少，但是却可能会增加“过拟合”的情况。因此，复杂的模型并不总是带来更好的结果。

技巧使用

数据增加

我们在单独考虑进化前的CP值跟进化后CP值之间的关系，并且在只有10个数据集的情况下进行模型设计。因此需要数据集的数量，并进行可视化，如图1-3所示

图1-3 数据集可视化

显然，在增加数据后，整个数据的分布就完全不是一条直线能够去拟合的。如果你对数据足够敏感的话，会发现神奇宝贝的物种对整个数据分布其很大影响，如图1-4所示；

图1-4 物种对数据集分布影响

正则化（Regularization）

如果我们不是神奇宝贝的专家，那么依旧可行的方法是将所有你能够想到的属性都加到模型中，去设计出一个非常复杂的模型。通常，复杂的模型容易出现过拟合。当出现过拟合时，该怎么办？

对Loss Function进行调整，之前设定的损失函数为（2），现在我们增加多个属性，并对（2）进行调整

其中，前一项表示实际值和训练集之间的误差，而加入后一项的目的在于使w_i尽可能小；使w_i尽可能小是为了使得整个损失函数的平滑性更好。平滑性指的是当函数的输入发生变化时，对函数输出的变化尽可能小；因此，平滑性可以使得当训练集中存在噪音时，这些噪音数据对整个模型的影响会比较小。

图1-5 正则化对训练和测试的影响

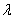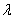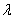从图1-5我们发现，当的值越大，训练误差也就增加，这是因为当值越大，对整个损失函数的值影响越大；当的值越大，测试误差是先减少后增加，我们希望模型的平滑性可以适当增加，但不用过于平滑。因为，直线是最平滑的，但是最平滑的直线却什么都表示不了。

增加正则化是使损失函数的平滑性更好，因此后一项不需要写成，因为增加b并不会改变函数的平滑性，只是使函数上下移动而已。

参考资料

[1]机器学习-李宏毅