对Tarjan——有向图缩点算法的理解

　　开始学tarjan的时候，有关无向图的割点、桥、点双边双缩点都比较容易地理解了，唯独对有向图的缩点操作不甚明了。通过对luoguP2656_采蘑菇一题的解决，大致搞清了tarjan算法的正确性。

　　首先放出有向图缩点tarjan函数的写法：

1. void tarjan(int u) {
2. dfn[u] = low[u] = ++timer;
3. sta[++stp] = u, ins[u] = true;
4. for (int i = head[u]; i; i = edge[i].nxt) {
5. int v = edge[i].to;
6. if (!dfn[v]) {
7. tarjan(v);
8. low[u] = min(low[u], low[v]);
9. } else if (ins[v])
10. low[u] = min(low[u], dfn[v]);
11. }
12. //////////////分割线////////////////
13. if (dfn[u] == low[u]) {
14. ++cnt;
15. int x;
16. do {
17. x = sta[stp--];
18. c[x] = cnt;
19. ins[x] = false;

} while (x != u);

1. }
2. }

　　问题主要出在函数的第二部分。遍历完u点的所有边后，第一，为什么将(dfn[u] == low[u])作为构成强连通分量的判定条件？第二，为什么此刻留在栈中的在u之后遍历的点能够构成一个强连通分量？

　　我们先来考虑一个强连通分量的特征。当有向图中一些点构成的集合是强连通的，当且仅当这部分图满足其中任意两点u、v互通。容易联想到，具有这个特征的典型结构还有有向环；实际上，环是最简单的强连通图，而（感性上）任意一个强连通分量都可以理解成是若干个互通的简单环所构成的。这是一个很重要的想法。笔者认为把复杂的强连通分量简化为环来理解，可以较容易地说明tarjan算法的正确性。

　　现在我们用两个简单的示意图来说明问题。

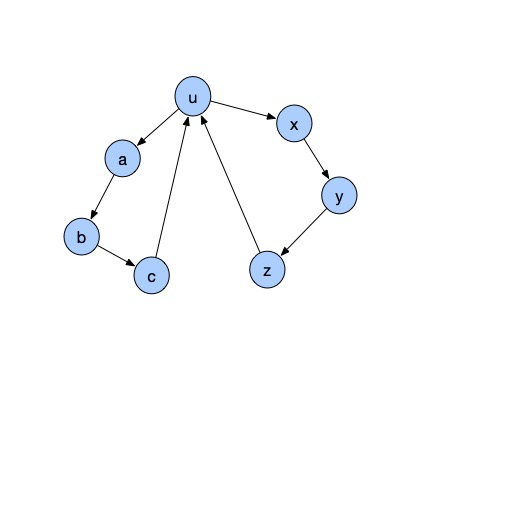
如上图，图一表示最简单的环情况，u是当前tarjan函数的起点。我们首先递归地将a、b、c入栈，发现三者的low值都指向了其上的u点，而不是它们自身。tarjan算法对条件(dfn[u] == low[u])的阐述是：满足该条件的u，是某个强连通分量的“根”；换言之，以u为根的搜索子树共同构成一个强连通分量。那么，我们观察这个结论的正确性何在。

1、对于该子树内的两点，若满足i点的时间戳大于j点，则i一定可以通过“前向边”（搜索边）连通至j点，这是显然的。

2、那么，为什么j点又可以通往i点呢？这就是判断条件(dfn[u] == low[u])的由来。显然，j点可以经由最后c点返回u点的那一条边，再从根u沿着前向边到达任意一个i点。

　　同时，我们可以说明以u为根的原因：如果我们在脑补一条边c-->a，那么a、b、c三点也是强连通的，但是这个连通部分又与u强连通，那么这三点构成的集合便不能成为（极大）强连通分量，a不是“根”。反之，若以u为根的子树不能回溯到还在栈中的更高点而仅能到达u，则这个分量一定是完整的。

　　图二为子树含两个环的情况，可以认为是更复杂的强连通分量结构。依然，对子树中任意一点v都可以返回到u，然后到达分量中的任意一点，则两个环共同与u构成强连通分量。实际上，任意的强连通结构都符合这个特征，我们总能沿着某条路径回到根，然后到达任意点，而这正是强连通分量的定义。

　　最后，联想到维护栈的意义：若某些点已经被遍历过而不在栈中，则其参与构成的强连通分量必然已达到最大，不可能与栈中剩余点强连通。典型的例子是横叉边：由当前点可以回到上一个强连通分量中，而那个分量却不存在边能到达当前点，否则这个点早就在那个分量中就被前向边遍历过了。而对于子树中已经弹出的点，一定是各自构成了较小的强连通分量：因为一定存在某个子节点v，使得(dfn[v] == low[v])，即其子树不能回溯到更广的分量范围中。

　　可能写得有些啰嗦，不太好明白（只有我自己知道我在说什么），所以欢迎有问题或者其他想法的同学在评论区交流。