WPF -- 一种直线识别方案

本文介绍一种直线的识别方案。

步骤

1. 使用最小二乘法回归直线：

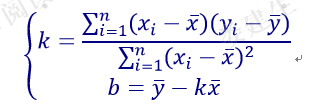
1. 得到直线方程y=kx+b后，计算所有点到直线的距离，若在阈值范围内，认为是直线。

实现

/// <summary>
/// 最小二乘法求回归直线方程
/// </summary>
/// <param name="points">输入数据</param>
/// <param name="k">直线斜率</param>
/// <param name="b">直线截距</param>
/// <param name="type">直线类型 1：水平线 2：垂直线 3：一般直线</param>
/// <returns></returns>
public static bool IsLine(List<Point> points, out double k, out double b, out int type)
{
    k = 0;
    b = 0;
    type = 0;
    if (points.Count < 2) return false;
    double averageX = 0, averageY = 0, n = 0;
    n = points.Count;
    foreach (Point p in points)
    {
        averageX += p.X;
        averageY += p.Y;
    }
    averageX /= n;
    averageY /= n;
    double numerator = 0, denominator = 0;
    foreach (Point p in points)
    {
        numerator += (p.X - averageX) * (p.Y - averageY);
        denominator += (p.X - averageX) * (p.X - averageX);
    }
    if (numerator == 0) //平行于X轴为水平线，返回纵坐标平均值
    {
        b = averageY;
        type = 1;
    }
    else if (denominator == 0)//平行于Y轴为垂直线，返回横坐标平均值
    {
        b = averageX;
        type = 2;
    }
    else
    {
        type = 3;
    }
    k = numerator / denominator;
    b = averageY - k * averageX;
    foreach (Point p in points)
    {
        dis = GetPoint2LineDistance(p, k, b, type);
        if (dis > MAX_POINT_LINE_DIS) return false; //点到拟合直线距离过大
    }
    return true;
}
/// <summary>
/// 计算点到直线的距离
/// </summary>
/// <param name="p">待计算点</param>
/// <param name="k">直线斜率</param>
/// <param name="b">直线截距</param>
/// <param name="type">直线类型 1：水平线 2：垂直线 3：一般直线</param>
/// <returns>距离</returns>
private static double GetPoint2LineDistance(Point p, double k, double b, int type)
{
    if (type == 1)
    {
        return Math.Abs(p.Y - b);
    }
    else if (type == 2)
    {
        return Math.Abs(p.X - b);
    }
    else
    {
        double numerator = 0, denominator = 0;
        numerator = Math.Abs(k * p.X - p.Y + b);
        denominator = Math.Sqrt(k * k + 1);
        return numerator / denominator;
    }
}