洛谷-P1439 【模板】最长公共子序列 (DP,离散化)

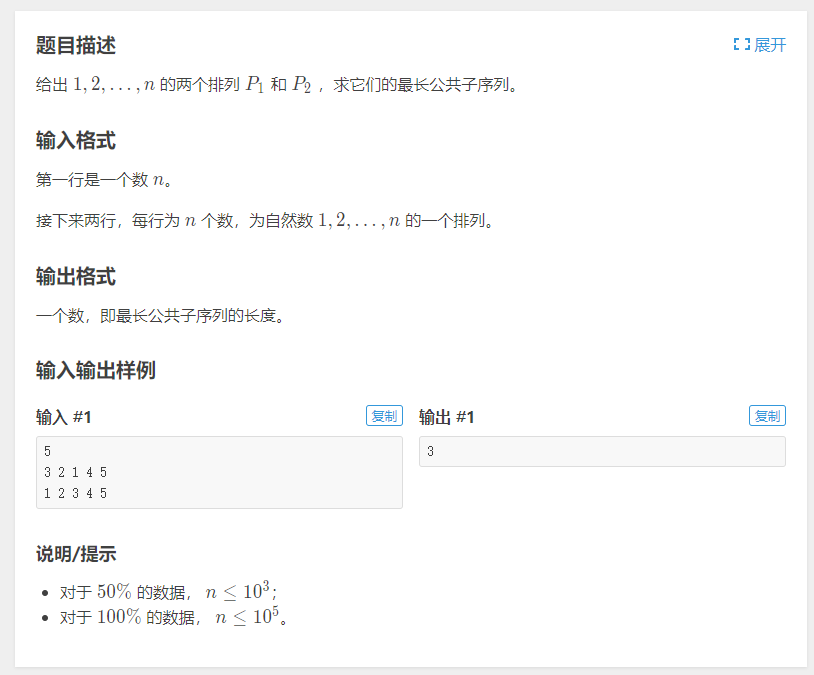
• 题意:给两个长度为\(n\)的全排列,求他们的LCS

• 题解:这题给的数据范围到\(10^5\),用\(O(n^2)\)的LCS模板过不了,但由于给的是两个全排列,他们所含的元素都是一样的,所以,我们以第一个串为模板,第二个串的每一个元素都能对应到第一个串的元素的位置,第二串对映后的最长上升子序列,就是他们的LCS,也就是我们先离散化一遍,然后求一个LIS\((O(n logn))\)即可.

• 代码:

  #include <iostream>
  #include <cstdio>
  #include <cstring>
  #include <cmath>
  #include <algorithm>
  #include <stack>
  #include <queue>
  #include <vector>
  #include <map>
  #include <set>
  #include <unordered_set>
  #include <unordered_map>
  #define ll long long
  #define fi first
  #define se second
  #define pb push_back
  #define me memset
  const int N = 1e6 + 10;
  const int mod = 1e9 + 7;
  using namespace std;
  typedef pair<int,int> PII;
  typedef pair<long,long> PLL;
  
  int n;
  int x;
  int a[N],b[N];
  int mp[N];
  int v[N];
  int main() {
      ios::sync_with_stdio(false);
      cin>>n;
       for(int i=1;i<=n;++i){
           cin>>a[i];
           mp[a[i]]=i;
       }
       for(int i=1;i<=n;++i){
           cin>>x;
           b[i]=mp[x];
       }
  
       v[1]=b[1];
       int len=1;
       for(int i=2;i<=n;++i){
           if(b[i]>v[len]) v[++len]=b[i];
           else{
               int pos=lower_bound(v+1,v+1+len,b[i])-v;
               v[pos]=b[i];
           }
       }
       printf("%d\n",len);
      return 0;
  }