牛客算法周周练20 F.紫魔法师 (二分图染色)

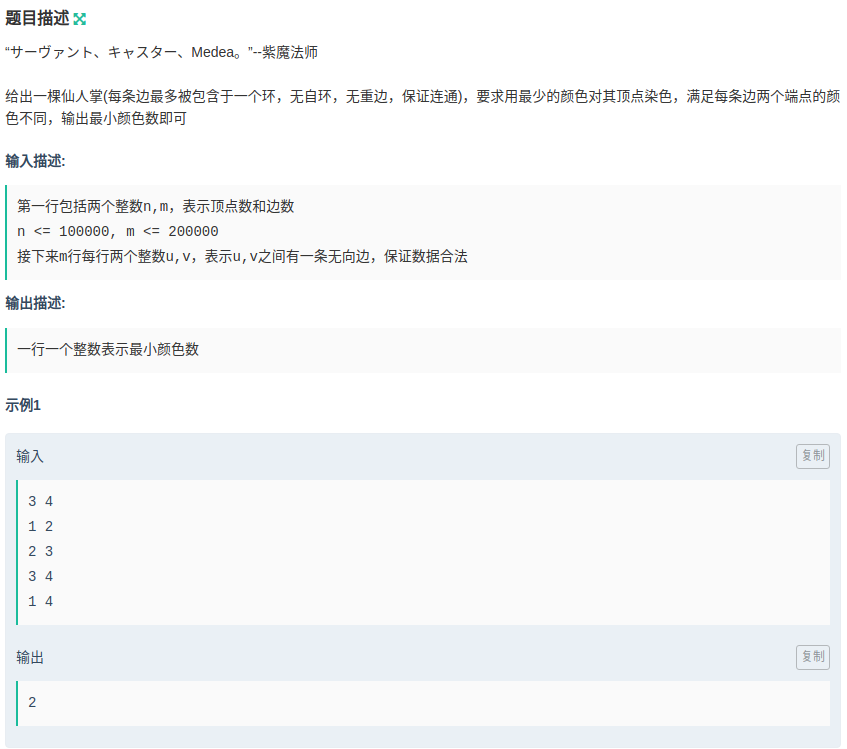
• 题意:给你一张图,对其染色,使得相连的点的颜色两两不同求,最少使用多少种颜色.

• 题解:首先,若\(n=1\),只需要一种.然后我们再去判断是否是二分图,对于二分图,两种颜色就够了,若不是二分图,也就是可能存在奇环的情况,那么三种颜色铁够了.所以题目就转化成了判断是否是二分图.

• 代码:

  int n,m;
  int u,v;
  int color[N];
  vector<int> V[N];
  
  bool dfs(int u,int c){
  	color[u]=c;
  
  	for(auto w:V[u]){
  		if(!color[w]){
  			if(!dfs(w,3-c)) return false;
  		}
  		else{
  			if(color[w]==c) return false;
  		}
  	}
  	return true;
  }
  
  int main() {
      //ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  	scanf("%d %d",&n,&m);
  
  	for(int i=1;i<=m;++i){
  		scanf("%d %d",&u,&v);
  		V[u].pb(v);
  		V[v].pb(u);
  	}
  	if(n==1){
  		puts("1");
  		return 0;
  	}
  	bool flag=true;
  	for(int i=1;i<=n;++i){
  		if(!color[i]){
  			if(!dfs(i,1)){
  				flag=false;
  				break;
  			}
  		}
  	}
  
  	if(!flag) puts("3");
  	else puts("2");
  
      return 0;
  }