Georgia and Bob(POJ 1704)

• 原题如下：
  Georgia and Bob

  Time Limit: 1000MS		Memory Limit: 10000K
  Total Submissions: 12712		Accepted: 4262

  Description

  Georgia and Bob decide to play a self-invented game. They draw a row of grids on paper, number the grids from left to right by 1, 2, 3, ..., and place N chessmen on different grids, as shown in the following figure for example: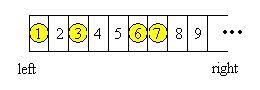 
  
  Georgia and Bob move the chessmen in turn. Every time a player will choose a chessman, and move it to the left without going over any other chessmen or across the left edge. The player can freely choose number of steps the chessman moves, with the constraint that the chessman must be moved at least ONE step and one grid can at most contains ONE single chessman. The player who cannot make a move loses the game.

  Georgia always plays first since "Lady first". Suppose that Georgia and Bob both do their best in the game, i.e., if one of them knows a way to win the game, he or she will be able to carry it out.

  Given the initial positions of the n chessmen, can you predict who will finally win the game?

  Input

  The first line of the input contains a single integer T (1 <= T <= 20), the number of test cases. Then T cases follow. Each test case contains two lines. The first line consists of one integer N (1 <= N <= 1000), indicating the number of chessmen. The second line contains N different integers P1, P2 ... Pn (1 <= Pi <= 10000), which are the initial positions of the n chessmen.

  Output

  For each test case, prints a single line, "Georgia will win", if Georgia will win the game; "Bob will win", if Bob will win the game; otherwise 'Not sure'.

  Sample Input

  2
  3
  1 2 3
  8
  1 5 6 7 9 12 14 17
  

  Sample Output

  Bob will win
  Georgia will win

• 题解：如果将棋子两两成对当成整体来考虑，就可以把这个游戏转为Nim游戏。如果棋子个数为偶数，把棋子从前往后两两组成一对，可以将每对棋子看成Nim中的一堆石子，石子的个数等于两个棋子之间的间隔。将右边的棋子向左移就相当于从Nim的石子堆中取走石子，将左边的棋子向左移，石子的数量增加了，这和Nim不同，但即便对手增加了石子的数量，只要将所加部分减回去就回到了原来的状态。因此，该游戏的胜负状态和所转移成的Nim的胜负状态一致。
• 代码：

   #include<cstdio>
   #include<algorithm>
  
   using namespace std;
  
   const int MAX_N=;
   int T, N, P[MAX_N];
  
   int main()
   {
       scanf("%d", &T);
       while (T>)
       {
           T--;
           scanf("%d", &N);
           for (int i=; i<N; i++)
           {
               scanf("%d", &P[i]);
           }
           if (N%==) P[N++]=;
           sort(P, P+N);
           int x=;
           for (int i=; i+<N; i+=)
           {
               x ^= (P[i+]-P[i]-);
           }
           if (x==) puts("Bob will win");
           else puts("Georgia will win");
       }
   }