noip2017奶酪

题目描述

现有一块大奶酪，它的高度为 h，它的长度和宽度我们可以认为是无限大的，奶酪 中间有许多 半径相同 的球形空洞。我们可以在这块奶酪中建立空间坐标系，在坐标系中， 奶酪的下表面为z=0，奶酪的上表面为z=h。

现在，奶酪的下表面有一只小老鼠 Jerry，它知道奶酪中所有空洞的球心所在的坐 标。如果两个空洞相切或是相交，则 Jerry 可以从其中一个空洞跑到另一个空洞，特别 地，如果一个空洞与下表面相切或是相交，Jerry 则可以从奶酪下表面跑进空洞；如果 一个空洞与上表面相切或是相交，Jerry 则可以从空洞跑到奶酪上表面。

位于奶酪下表面的 Jerry 想知道，在 不破坏奶酪 的情况下，能否利用已有的空洞跑 到奶酪的上表面去?

空间内两点P1​(x1​,y1​,z1​)、P2(x2​,y2​,z2​)的距离公式如下：

dist(P1​,P2​)=sqrt((x1​−x2​)^2+(y1​−y2​)^2+(z1​−z2​)^2​)

输入输出格式

输入格式：

每个输入文件包含多组数据。

的第一行，包含一个正整数 T，代表该输入文件中所含的数据组数。

接下来是 T 组数据，每组数据的格式如下： 第一行包含三个正整数 n,h 和 r，两个数之间以一个空格分开，分别代表奶酪中空 洞的数量，奶酪的高度和空洞的半径。

接下来的 n 行，每行包含三个整数 x,y,z，两个数之间以一个空格分开，表示空 洞球心坐标为(x,y,z)。

输出格式：

T 行，分别对应 T 组数据的答案，如果在第 i 组数据中，Jerry 能从下 表面跑到上表面，则输出Yes，如果不能，则输出No （均不包含引号）。

输入输出样例

输入样例#1： 复制

3
2 4 1
0 0 1
0 0 3
2 5 1
0 0 1
0 0 4
2 5 2
0 0 2
2 0 4

输出样例#1： 复制

Yes
No
Yes

说明

【输入输出样例 1 说明】

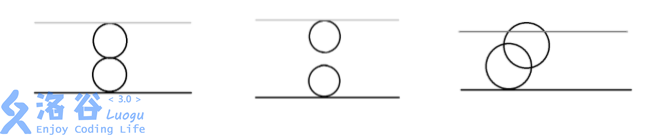
第一组数据,由奶酪的剖面图可见：

第一个空洞在(0,0,0)与下表面相切

第二个空洞在(0,0,4)与上表面相切 两个空洞在(0,0,2)相切

输出 Yes

第二组数据,由奶酪的剖面图可见：

两个空洞既不相交也不相切

输出 No

第三组数据,由奶酪的剖面图可见：

两个空洞相交 且与上下表面相切或相交

输出 Yes

【数据规模与约定】

对于 20%的数据,n=1,1≤h , r≤10,000,坐标的绝对值不超过 10,000。

对于 40%的数据,1≤n≤8, 1≤h , r≤10,000,坐标的绝对值不超过 10,000。

对于80%的数据, 1≤n≤1,000, 1≤h,r≤10,000,坐标的绝对值不超过10,000。

对于 100%的数据,1≤n≤1,000,1≤h,r≤1,000,000,000,T≤20,坐标的 绝对值不超过1,000,000,000。

 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<algorithm>
 using namespace std;
 int T,i,j,n,op,fa[],ta = ,to = ,di[],gao[];
 long long int h,r;
 struct node
 {
     long long int x;
     long long int y;
     long long int z;
 }a[];
 int find(int x)
 {
     if(fa[x] != x)
     {
         fa[x] = find(fa[x]);
     }
     return fa[x];
 }
 void lianjie(int x,int y)
 {
     x = find(x);
     y = find(y);
     fa[y] = x;
 }
 int main()
 {
     scanf("%d",&T);
     for(i = ;i <= T;i++)
     {
         op = ;
         to = ;
         ta = ;
         scanf("%d %lld %lld",&n,&h,&r);
         for(j = ;j <= n;j++)
         {
             fa[j] = j;
             scanf("%lld %lld %lld",&a[j].x,&a[j].y,&a[j].z);
             if(a[j].z - r <= )
             {
                 to++;
                 di[to] = j;
             }
             if(a[j].z + r >= h)
             {
                 ta++;
                 gao[ta] = j;
             }
             for(int k = ;k <= j;k++)
             {
                 if(sqrt((a[j].x - a[k].x) * (a[j].x - a[k].x) + (a[j].y - a[k].y) * (a[j].y - a[k].y) + (a[j].z - a[k].z) * (a[j].z - a[k].z)) <= r * )
                 {
                     lianjie(j,k);
                 }
             }
         }
         for(j = ;j <= ta;j++)
         {
             for(int k = ;k <= to;k++)
             {
                 if(find(di[k]) == find(gao[j]))
                 {
                     printf("Yes");
                     op = ;
                     break;
                 }
             }
             if(op == )
             break;
         }
         if(op == )
         printf("No");
         if(i != T)
         printf("\n");
     }
     return ;
 }

*****这是一个并查集，从保存下来可以通往顶部和底部的点，找他俩的公共爸爸，如果是一个则证明是这条路是连通哒，每一次都要搜索这个点和他之前的那些点是否连通哦。