luogu P2486 [SDOI2011]染色

树剖做法：
就是两个dfs+一个线段树
难度的取决基本==线段树的维护难度
所以对有点线段树基础的，树剖也不难做吧
这里操作有二
一：两点间路径染色
线段树的区间赋值操作
二：查询路径段的个数
考虑线段树如何做
我们发现两端区间的合并取决于他们相连接的那两个颜色
比如这张图

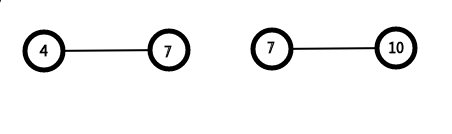
他两边区间合并的时候，完全就是左区间答案+右区间答案也就是2+2
但是这样

他们合并的答案就是2+2-1了也就是中间连接的两个颜色相同时要减1
明白了这个pushup也就不难写了
这里在说一下查询操作
由于是分开查询的，所以也有可能会中间相同而没有减1
这里就有点套路(技巧？)了，留给你们想吧
光线段树上就完事了吗，当然不是
树链剖分把树给剖了当然会有影响
我们再判断一下两条链之间是否颜色相同就可以了
好了,再不懂就去看一下代码吧

代码

cpp #include <bits/stdc++.h> #define FOR(i,a,b) for(int i=a;i<=b;++i) using namespace std; const int N=100007; int read() { int x=0,f=1;char s=getchar(); for(;s>'9'||s<'0';s=getchar()) if(s=='-') f=-1; for(;s>='0'&&s<='9';s=getchar()) x=x*10+s-'0'; return x*f; } int n,m,a[N],col[N],top[N],f[N],son[N],siz[N],dep[N],idx[N],cnt; struct node { int v,nxt; }e[N<<1]; int head[N],tot; void add_edge(int u,int v) { e[++tot].v=v; e[tot].nxt=head[u]; head[u]=tot; } void dfs1(int u,int fa) { dep[u]=dep[fa]+1; siz[u]=1; f[u]=fa; for(int i=head[u];i;i=e[i].nxt) { int v=e[i].v; if(v==fa) continue; dfs1(v,u); siz[u]+=siz[v]; if(siz[son[u]] < siz[v]) son[u]=v; } } void dfs2(int u,int topf) { idx[u]=++cnt; a[cnt]=col[u]; top[u]=topf; if(!son[u]) return; dfs2(son[u],topf); for(int i=head[u];i;i=e[i].nxt) if(!idx[e[i].v]) dfs2(e[i].v,e[i].v); } namespace seg_tree { #define ls (rt<<1) #define rs (rt<<1|1) struct node { int l,r,lc,rc; int sum,lazy; }e[N<<2]; void pushup(int rt) { if(ls&&rs) { e[rt].sum=e[ls].sum+e[rs].sum-(e[ls].rc==e[rs].lc); e[rt].lc=e[ls].lc; e[rt].rc=e[rs].rc; } else e[rt]=e[ls+rs]; } void build(int l,int r,int rt) { e[rt].l=l,e[rt].r=r; if(l==r) { e[rt].lc=e[rt].rc=a[l]; e[rt].sum=1; return; } int mid=(l+r)>>1; build(l,mid,ls); build(mid+1,r,rs); pushup(rt); } void tag(int rt,int k) { e[rt].lc=e[rt].rc=k; e[rt].sum=1; e[rt].lazy=k; } void pushdown(int rt) { if(e[rt].lazy) { tag(ls,e[rt].lazy); tag(rs,e[rt].lazy); e[rt].lazy=0; } } void modify(int L,int R,int k,int rt) { if(L<=e[rt].l&&e[rt].r<=R) { tag(rt,k); return; } pushdown(rt); int mid=(e[rt].l+e[rt].r)>>1; if(L<=mid) modify(L,R,k,ls); if(R>mid) modify(L,R,k,rs); pushup(rt); } node query(int L,int R,int rt) { if(L<=e[rt].l&&e[rt].r<=R) return e[rt]; pushdown(rt); int mid=(e[rt].l+e[rt].r)>>1; if(L<=mid && R>mid) { node a=query(L,R,ls),b=query(L,R,rs); node c; c.lc=a.lc; c.rc=b.rc; c.sum=a.sum+b.sum-(a.rc==b.lc); return c; } if(L<=mid) return query(L,R,ls); if(R>mid) return query(L,R,rs); } int ask(int L,int rt) { if(e[rt].l==e[rt].r) return e[rt].lc; pushdown(rt); int mid=(e[rt].l+e[rt].r)>>1; if(L<=mid) return ask(L,ls); else return ask(L,rs); } } void CC(int x,int y,int k) { while(top[x]!=top[y]) { if(dep[top[x]] < dep[top[y]]) swap(x,y); seg_tree::modify(idx[top[x]],idx[x],k,1); x=f[top[x]]; } if(dep[x]>dep[y])swap(x,y); seg_tree::modify(idx[x],idx[y],k,1); } void QQ(int x,int y) { int ans=0; while(top[x]!=top[y]) { if(dep[top[x]] < dep[top[y]]) swap(x,y); ans+=seg_tree::query(idx[top[x]],idx[x],1).sum; ans-=(seg_tree::ask(idx[top[x]],1)==seg_tree::ask(idx[f[top[x]]],1)); x=f[top[x]]; } if(dep[x]>dep[y])swap(x,y); ans+=seg_tree::query(idx[x],idx[y],1).sum; printf("%d\n", ans); } int main() { n=read(),m=read(); FOR(i,1,n) col[i]=read(); FOR(i,2,n) { int x=read(), y=read(); add_edge(x,y); add_edge(y,x); } dfs1(1,0); dfs2(1,1); seg_tree::build(1,n,1); FOR(i,1,m) { char s=getchar(); while(s==' '||s=='\n') s=getchar(); int x=read(), y=read(), z; if(s=='C') z=read(),CC(x,y,z); else QQ(x,y); } return 0; }l