codeforces 848B Rooter's Song 思维题

http://codeforces.com/problemset/problem/848/B

给定一个二维坐标系，点从横轴或纵轴垂直于发射的坐标轴射入(0,0)-(w,h)的矩形空间。给出点发射的坐标轴，位置，延迟时间，发生碰撞则交换方向。求最后每个点的射出位置。

首先我们观察能得出两个结论，1. 类似蚂蚁爬树枝的问题，相遇只会交换方向，所以最后的射出点集只会因为碰撞而改变动点与射出点的对应关系，而不会增加减少射出点集。2.我们根据其射入位置和延迟时间可以计算出一个值v=pos-time，只有这个值相等才可能发生碰撞。

这样我们可以把所有点根据值v分成若干个集合，每个集合互不干涉，对于一个集合的射出点集，我们只要处理内部的对应关系即可。

首先画一张图片，代表一个集合的所有点，因为v相等，只要在图中的射线可以相遇一定会碰撞。

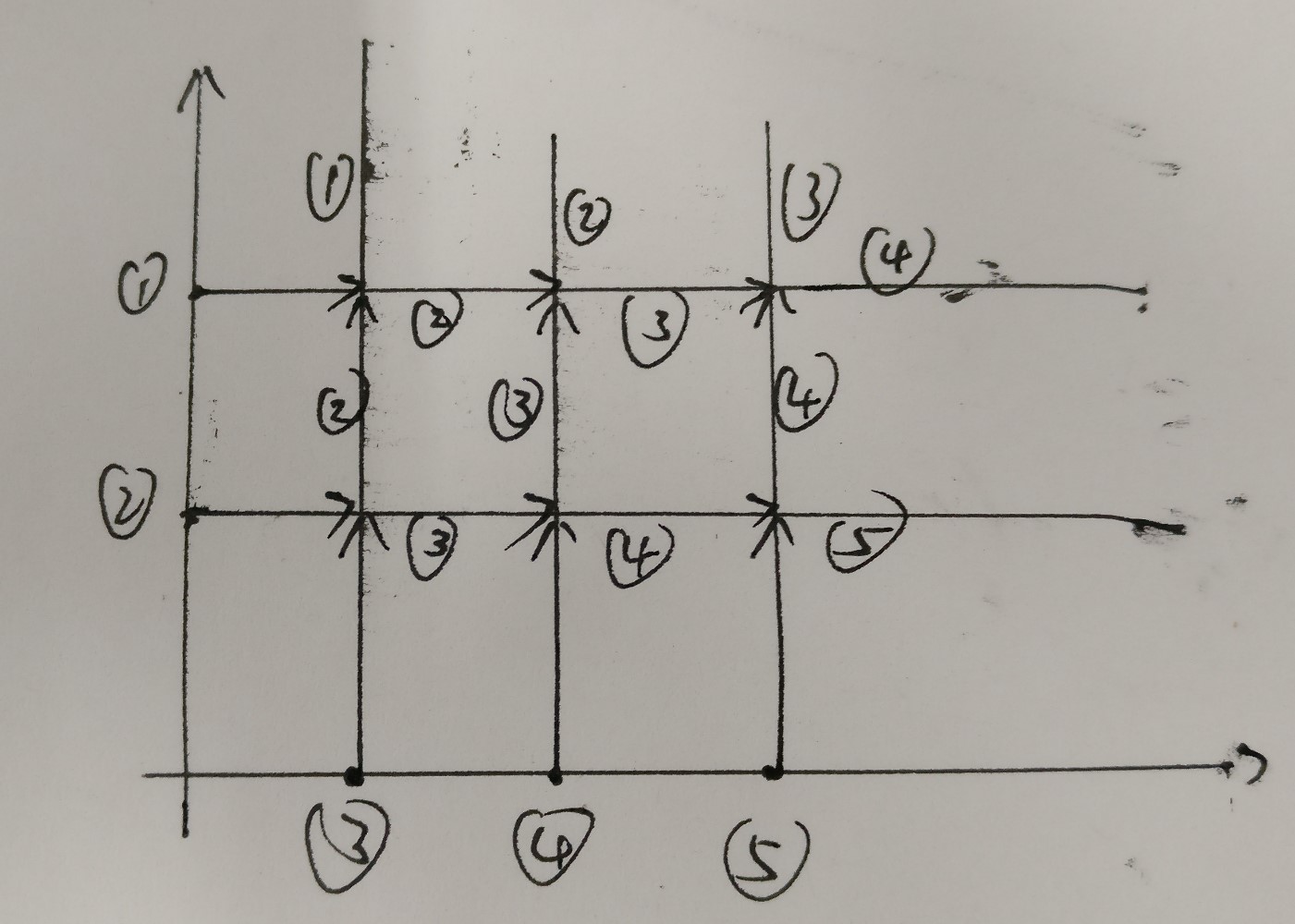
可见一个点从出发后，将依次交替遭遇另一个轴的点(数量为siz0)和本轴坐标大于等于本身的点(数量为siz1)。最终不再碰撞时的方向我们可以很容易地通过siz0,siz1推出来，而方向与最后一次碰撞的点相同（当与当前方向的平行的坐标轴发射的动点数量用尽时就不再碰撞了）。

这样每个点都可以在O(1)或O(log(n))下求出射出位置。因为需要排序预处理，所以要不要优化到O(1)并不是很重要。

#include <iostream>
#include <string>
#include <algorithm>
#include <vector>
#include <cmath>
#include <cstring>
#include <set>
#include <map>
#include <queue>
#define LL long long
using namespace std;
const LL N = ;
LL n, w, h;
struct node
{
    LL g, p, t;
};
map<LL, vector<LL> > g[];
node v[N];
int main()
{
    cin.sync_with_stdio(false);
    while (cin >> n>>w>>h)
    {
        g[].clear(), g[].clear();

        for (int i = ; i < n; i++)
        {
            node temp;
            cin >> temp.g >> temp.p >> temp.t;
            temp.g--;
            g[temp.g][temp.p - temp.t].push_back(temp.p);
            v[i] = temp;
        }
        for (map<LL, vector<LL> >::iterator it = g[].begin(); it != g[].end(); it++)
            sort(it->second.begin(), it->second.end());
        for (map<LL, vector<LL> >::iterator it = g[].begin(); it != g[].end(); it++)
            sort(it->second.begin(), it->second.end());
        for (int i = ; i < n; i++)
        {
            node e = v[i];
            int dg;
            if (e.g == )
            {
                dg = ;
                LL siz[];
                siz[e.g]= g[e.g][e.p - e.t].end() - lower_bound(g[e.g][e.p - e.t].begin(), g[e.g][e.p - e.t].end(), e.p);
                siz[dg] = g[dg][e.p - e.t].size();
                LL miz = min(siz[], siz[]);
                if (siz[e.g] <= siz[dg])
                    cout << w << ' ' << g[dg][e.p - e.t][miz-] << endl;
                else
                    cout << g[e.g][e.p - e.t][g[e.g][e.p - e.t].size()-siz[e.g]+miz] << ' ' << h << endl;
            }
            else
            {
                dg = ;
                LL siz[];
                siz[e.g] = g[e.g][e.p - e.t].end() - lower_bound(g[e.g][e.p - e.t].begin(), g[e.g][e.p - e.t].end(), e.p);
                siz[dg] = g[dg][e.p - e.t].size();
                LL miz = min(siz[], siz[]);
                if (siz[e.g] <= siz[dg])
                    cout << g[dg][e.p - e.t][miz-]<<' '<<h << endl;
                else
                    cout << w<<' '<<g[e.g][e.p - e.t][g[e.g][e.p - e.t].size() - siz[e.g] + miz]<<endl;
            }
        }

    }

    return ;
}