Lambert漫反射brdf=Albedo/pi。

推导：

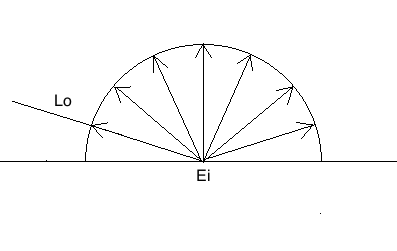
如图，设Lambert面元获得入射照度Ei，各方向均匀释放亮度，每个方向释放的亮度都是Lo。

又设此表面反射率为Albedo，根据反射率定义

Albedo=Eo/Ei

=（因为Lo各方向相同）=（为半球）

=(Lo*pi)/Ei

所以

brdf=Lo/Ei=Albedo/pi

注：

半球cos积分等于pi的计算过程：

作代换dw=sin(theta)*dtheta*dphi，则

或者也可以用直角坐标系来算，但比较繁：

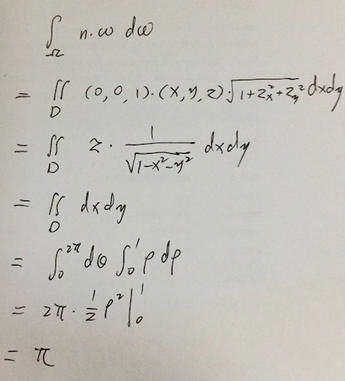
Lambert漫反射的BRDF的更多相关文章

  1. Lambert漫反射.BLinnPhong及Phong模型 Unity自带的在Lighting.cginc里

    1.漫反射 此模型属于经验模型,主要用来简单模拟粗糙物体表面的光照现象 此模型假设物体表面为理想漫反射体(也就是只产生漫反射现象,也成为Lambert反射体),同时,场景中存在两种光,一种为环境光,一 ...

  2. pbr若干概念

    pbr基于辐射传输理论,最基本的一个观点是:一切皆光源--任何一个面元既是光能接收器,也是光能发射器. 光通(flux):单位时间内通过某一面积的光能,单位W(瓦特),用表示. 可见,光通其实就是功率 ...

  3. 漫反射和Lambert模型

    粗糙的物体表面向各个方向等强度地反射光,这种等同地向各个方向散射的现象称为光的漫反射(diffuse reflection).产生光的漫反射现象的物体表面称为理想漫反射体,也称为朗伯(Lambert) ...

  4. 【三】材质反射属性模型BRDF

    双向反射分布函数(BRDF:Bidirecitonal Reflectance Distribution Function) 用来描述物体表面对光的反射性质 预备知识 BRDF的定义和性质 BRDF模 ...

  5. Microfacet模型采样下的brdf

    本文前言 在学习图形学(games101 from bilibili)的时候,也遇到了像这样的问题,Cook-Torrance模型无法实现粗糙度为0时,物体微表面呈现绝对镜面的效果(呈现出一面镜子), ...

  6. Lambert模型

    [Lambert模型] 漫反射光的强度近似地服从于Lambert定律,即漫反射光的光强仅与入射光的方向和反射点处表面法向夹角的余弦成正比. 由此可以构造出Lambert漫反射模型:Idiffuse = ...

  7. 精确光源（Punctual Light Sources）

    <Physically-Based Shading Models in Film and Game Production>(SIGGRAPH 2010 Course Notes) (地址: ...

  8. Unity3D for VR 学习(9): Unity Shader 光照模型 (illumination model)

    关于光照模型 所谓模型,一般是由学术算法发起, 经过大量实际数据验证而成的可靠公式 现在还记得2009年做TD-SCDMA移动通信算法的时候,曾经看过自由空间传播模型(Free space propa ...

  9. 由浅入深学习PBR的原理和实现

    目录 一. 前言 1.1 本文动机 1.2 PBR知识体系 1.3 本文内容及特点 二. 初阶:PBR基本认知和应用 2.1 PBR的基本介绍 2.1.1 PBR概念 2.1.2 与物理渲染的差别 2 ...

随机推荐

  1. BZOJ1202 [HNOI2005]狡猾的商人 spfa

    欢迎访问~原文出处——博客园-zhouzhendong 去博客园看该题解 题目传送门 - BZOJ1202 题意概括 有一个数列,共n个数字. 告诉你m个区间和,问是否矛盾. 数据组数<=100 ...

  2. 对于pycharm和vscode下，从外部复制文本内容为python字符串内容是会自动加\u202a解决办法

    先来看下这个python3源代码,表面上看没有语法毛病,如果源代码字符串内容是手动复制过来的文本内容,在pycharm和vscode下始终提示: pywintypes.error: (2, 'Shel ...

  3. POJ 1222 熄灯问题【高斯消元】

    <题目链接> 题目大意: 有一个5*6的矩阵,每一位是0或者1. 没翻转一位,它的上下左右的数字也为改变.(0变成1,1变成0).要把矩阵中所有的数都变成0.求最少翻转次数的方案,输出矩阵 ...

  4. HDU 3746 Cyclic Nacklace (KMP求循环节问题)

    <题目链接> 题目大意: 给你一个字符串,要求将字符串的全部字符最少循环2次需要添加的字符数. [>>>kmp next函数 kmp的周期问题]  #include &l ...

  5. beta到production版本上线

    1.beta版本到production上线,production要发到预发布测试一下避免配置问题导致发布异常.

  6. 电商sku商品推荐

    1.逻辑回归LR进行实时离线三级品类训练. 2.通过用户对于实时.离线三级品类的偏好进行召回. 3.通过人的特征.sku特征.人sku交互特征.以及位置手机特征通过gbdt模型进行点击量预估.

  7. 洛谷.3834.[模板]可持久化线段树(主席树 静态区间第k小)

    题目链接 //离散化后范围1~cnt不要错 #include<cstdio> #include<cctype> #include<algorithm> //#def ...

  8. 正则表达式(特殊字符)/Xpath语法/CSS选择器

    正则表达式(特殊字符) ^ 开头 '^b.*'----以b开头的任意字符 $ 结尾 '^b.*3$'----以b开头,3结尾的任意字符 * 任意长度(次数),≥0 ? 非贪婪模式,非贪婪模式尽可能少的 ...

  9. 【linux】linux修改open file 大小

    使用下面命令可以查看openfile数量 ulimit -a linux修改open file 大小,修改步骤如下: 1>修改file-max 修改文件: vi /etc/sysctl.conf ...

  10. electron实现类似QQ来新消息时的闪烁与任务栏窗口提醒

    公司项目有一款带即时聊天.群组功能的APP,因为要给客服人员使用,需要开发PC版本.之前使用C#开发过一个PC版本,但是C#的UI这一块支持的不太好,而且升级比较麻烦,我就牵头基于Electron去实 ...