EM算法——Expectation-Maximization
最大似然估计
一个栗子:假如去赌场,但是不知道能不能赚钱,你就在门口堵着出来一个人就问一个赚了还是赔了,如果问了5个人都说赚了,那么你就会认为,赚钱的概率肯定是非常大的。
已知:(1)样本服从分部的模型,(2)观测到的样本
求解:模型的参数
总的来说:极大似然估计就是用来估计模型参数的统计学方法
最大似然的数学问题(100名学生的身高问题)
样本集X = {x1, x2 ,...,xN} N = 100
概率密度:p(xi|θ)抽到男生i(的身高)的概率
θ是服从分部的参数
独立同分布:同时抽到这100个男生的概率就是他们各自概率的乘积
最大似然函数:
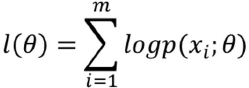 (对数是为了乘法转加法)
(对数是为了乘法转加法)
什么样的参数θ能够使得出现当前这批样本的概率最大
已知某个随机样本满足某种概率分布,但是其中具体的参数不清楚,参数估计就是通过若干次试验,观察其结果,利用结果推出参数的大概值。
问题又难了一步
现在这100个人中,不光有男生,还有女生(2个类别,2种参数)
男生和女生的身高都服从高斯分布,但是参数不同(均值,方差)
用数学的语言描述:抽取得到的每个样本都不知道是从哪个分布抽取的
求解目标:男生和女生对应的身高的高斯分布的参数是多少
加入隐变量
用Z = 0或Z = 1标记样本来自哪个分部,则Z就是隐变量
最大似然函数:
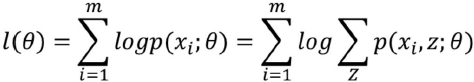
求解:在给定初始值情况下进行迭代求解
EM算法
EM算法推导:
问题:样本集{x(1),...,x(m)},包含m个独立的样本。其中每个样本i对应的类别z(i)是未知的,所以很难用最大似然求解。
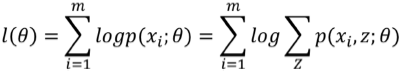
上式中,要考虑每个样本在各个分布中的情况。本来正常求偏导就可以了,但是现在log后面还有求和,这就难解了!
右式分子分母同时乘:
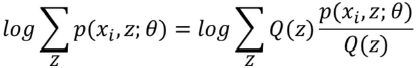
这么做就是为了凑Jensen不等式(Q(z)是Z的分布函数)
Jensen不等式
设f是定义域为实数的函数,如果对于所有的实数x。
如果对于所有的实数x,f(x)的二次导数大于等于0,那么f是凸函数。
如果f是凸函数,X是随机变量,那么:E[f(X)] > = f(E[X])
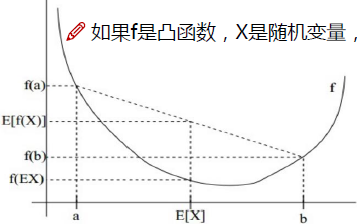
实线f是凸函数,X有0.5的概率是a,有0.5的概率是b,X的期望值就是a和b的中值了
Jensen不等式应用于凹函数时,不等号方向反向
由于:
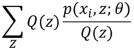 是
是 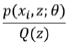 的期望
的期望
假设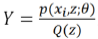 则:
则: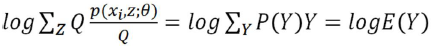
可得:
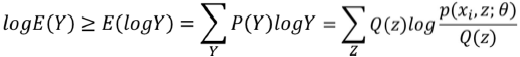
结论:
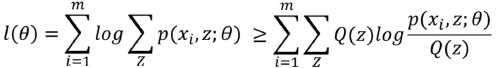
下届比较好求,所以我们要优化这个下界来使得似然函数最大
优化下届,迭代到收敛
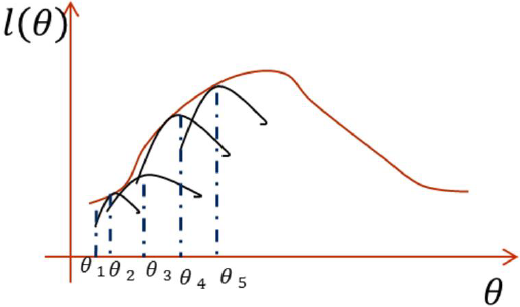
Jensen中等式成立的条件是随机变量是常数:
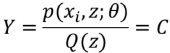
Q(z)是z的分部函数:
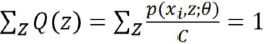
所有的分子和等于常数C(分母相同)
Q(z)求解

由上式可得C就是p(xi,z)对z求和
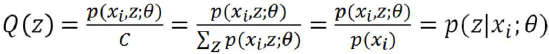
Q(z)代表第i个数据是来自zi的概率
EM算法流程
初始化分布参数Θ
E-step:根据参数Θ计算每个样本属于zi的概率(也就是Q)
M-step:根据Q,求出含有Θ的似然函数的下界并最大化它,得到新的参数Θ
不断的迭代更新
GMM(高斯混合模型)
数据可以看作是从数个Gaussian Distribution中生成出来的
GMM由K个Gaussian分布组成,每个Gaussian称为一个“Component”
类似k-means方法,求解方式跟EM一样
不断的迭代更新
EM算法——Expectation-Maximization的更多相关文章
- EM算法(Expectation Maximization Algorithm)
EM算法(Expectation Maximization Algorithm) 1. 前言 这是本人写的第一篇博客(2013年4月5日发在cnblogs上,现在迁移过来),是学习李航老师的< ...
- EM算法(Expectation Maximization)
1 极大似然估计 假设有如图1的X所示的抽取的n个学生某门课程的成绩,又知学生的成绩符合高斯分布f(x|μ,σ2),求学生的成绩最符合哪种高斯分布,即μ和σ2最优值是什么? 图1 学生成绩的分 ...
- EM算法(Expectation Maximization Algorithm)初探
1. 通过一个简单的例子直观上理解EM的核心思想 0x1: 问题背景 假设现在有两枚硬币Coin_a和Coin_b,随机抛掷后正面朝上/反面朝上的概率分别是 Coin_a:P1:-P1 Coin_b: ...
- 简单理解EM算法Expectation Maximization
1.EM算法概念 EM 算法,全称 Expectation Maximization Algorithm.期望最大算法是一种迭代算法,用于含有隐变量(Hidden Variable)的概率参数模型的最 ...
- EM 算法 Expectation Maximization
- EM(Expectation Maximization)算法
EM(Expectation Maximization)算法 参考资料: [1]. 从最大似然到EM算法浅解 [2]. 简单的EM算法例子 [3]. EM算法)The EM Algorithm(详尽 ...
- 最大期望算法 Expectation Maximization概念
在统计计算中,最大期望(EM,Expectation–Maximization)算法是在概率(probabilistic)模型中寻找参数最大似然估计的算法,其中概率模型依赖于无法观测的隐藏变量(Lat ...
- 机器学习-EM算法
最大期望算法 EM算法的正式提出来自美国数学家Arthur Dempster.Nan Laird和Donald Rubin,其在1977年发表的研究对先前出现的作为特例的EM算法进行了总结并给出了标准 ...
- 数据挖掘十大经典算法(5) 最大期望(EM)算法
在统计计算中,最大期望(EM,Expectation–Maximization)算法是在概率(probabilistic)模型中寻找参数最大似然估计的算法,其中概率模型依赖于无法观测的隐藏变量(Lat ...
- EM算法及其推广
概述 EM算法是一种迭代算法,用于含有隐变量(hidden variable)的概率模型参数的极大似然估计,或极大后验概率估计. EM算法的每次迭代由两步组成:E步,求期望(expectation): ...
随机推荐
- linux常用命令:touch 命令
linux的touch命令不常用,一般在使用make的时候可能会用到,用来修改文件时间戳,或者新建一个不存在的文件. 1.命令格式: touch [选项]... 文件... 2.命令参数: -a ...
- ad 原件布局布线基本规则
一.原件布局基本规则 1.按照电路模块进行布局,电路中的元件应该采用集中就近原则,同时数字电路和模拟电路分开: 2.定位孔.标准孔等周围1.27mm内不得贴元器件,安装孔周围3.5mm不得特装元件 3 ...
- 在centos上搭建JavaWeb环境(jdk+mysql+tomcat)
1.安装OpenJDK yum list java* -openjdk* -y java -version 2.安装Tomcat cd /usr/local wget https://mc.qclou ...
- 像黑客一样使用Linux命令行(转载)
阅读目录 前言 使用 tmux 复用控制台窗口 在命令行中快速移动光标 在命令行中快速删除文本 快速查看和搜索历史命令 快速引用和修饰历史命令 录制屏幕并转换为 gif 动画图片 总结 回到顶部 前言 ...
- Java 多线程并发编程面试笔录一览
知识体系图: 1.线程是什么? 线程是进程中独立运行的子任务. 2.创建线程的方式 方式一:将类声明为 Thread 的子类.该子类应重写 Thread 类的 run 方法 方式二:声明实现 Runn ...
- 源码部署pxc集群
想了想还是研究一下怎么源码安装pxc吧,毕竟很多组件都是源码安装的. 环境: yum install -y boost-devel libodb-boost-devel check-devel ope ...
- Prometheus监控学习笔记之PromQL操作符
0x00 二元运算符 Prometheus 的查询语言支持基本的逻辑运算和算术运算.对于两个瞬时向量, 匹配行为可以被改变. 算术二元运算符 在 Prometheus 系统中支持下面的二元算术运算符: ...
- yii2项目中运行composer 过程中遇到的问题
问题1: Your requirements could not be resolved to an installable set of packages 则表明 未安装fxp/composer-a ...
- 单元测试Mock框架Powermockito 【mockito1.X】
<properties> <project.build.sourceEncoding>UTF-8</project.build.sourceEncoding> &l ...
- P2147 [SDOI2008]洞穴勘测(LCT)
P2147 [SDOI2008]洞穴勘测 裸的LCT. #include<iostream> #include<cstdio> #include<cstring> ...
