洛谷 3295 [SCOI2016]萌萌哒——并查集优化连边

题目：https://www.luogu.org/problemnew/show/P3295

当要连的边形如 “一段区间内都是 i 向 i+L 连边” 的时候，用并查集优化连边。

在连边的时候，如果要连的区间已经有一部分连成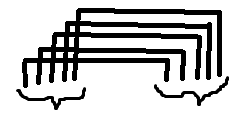这个样子了，就希望跳过这一段。

想倍增那样跳过已经连好的部分。用并查集实现。

建 logn 个并查集，第 i 个并查集里 x 和 y 连通表示 \( [x,x+2^i-1] \) 和 \( [y,y+2^i-1] \) 已经连成了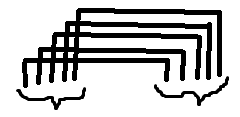的样子。

那么要连 \( [l1,r1] \) 和 \( [l2,r2] \) 的时候，用 RMQ 的思想把它拆成连 \( [l1,l1+bin[k]-1] \) 和 \( [l2,l2+bin[k]-1] \) 与连 \( [r1-bin[k]+1,r1] \) 和 \( [r2-bin[k]+1,r2] \) 两次操作（其中 bin[k] 是 小于等于 (r-l+1) 的最大的2的整次幂）；在第 t 层的并查集连的时候，如果该层的 x 和 y 已经连通，就直接返回；不然就连通该层的 x 和 y ，然后递归进 t-1 层连；递归的时候会分裂成两部分，即 \( mrg(t-1,l,r) \) 和 \( mrg(t-1,l+bin[t-1],r+bin[t-1]) \) 。

这样就跳过了已经连好的部分。最后的真实连通情况就是第 0 层的情况。

每层并查集最多连 n 次，所以均摊复杂度 nlogn 。

#include<cstdio>
#include<cstring>
#include<algorithm>
#define ll long long
using namespace std;
int rdn()
{
  int ret=;bool fx=;char ch=getchar();
  while(ch>''||ch<''){if(ch=='-')fx=;ch=getchar();}
  while(ch>=''&&ch<='')ret=ret*+ch-'',ch=getchar();
  return fx?ret:-ret;
}
const int N=1e5+,K=,mod=1e9+;
int pw(int x,int k)
{int ret=;while(k){if(k&)ret=(ll)ret*x%mod;x=(ll)x*x%mod;k>>=;}return ret;}

int n,m,lg[N],bin[K],fa[K][N];
int fnd(int t,int a)
{return fa[t][a]==a?a:fa[t][a]=fnd(t,fa[t][a]);}
void mrg(int t,int x,int y)
{
  int u=fnd(t,x), v=fnd(t,y);
  if(u!=v)
    {
      fa[t][u]=v;
      if(!t)return;
      mrg(t-,x,y); mrg(t-,x+bin[t-],y+bin[t-]);
    }
}
int main()
{
  n=rdn();m=rdn();
  for(int i=;i<=n;i++)lg[i]=lg[i>>]+;
  bin[]=;for(int i=;i<=lg[n];i++)bin[i]=bin[i-]<<;
  for(int t=;t<=lg[n];t++)
    for(int i=;i<=n;i++)fa[t][i]=i;
  for(int i=,l1,r1,l2,r2,d,t;i<=m;i++)
    {
      l1=rdn();r1=rdn();l2=rdn();r2=rdn();
      d=lg[r1-l1+]; r1=r1-bin[d]+; r2=r2-bin[d]+;
      mrg(d,l1,l2); mrg(d,r1,r2);
    }
  int cnt=;
  for(int i=;i<=n;i++)if(fnd(,i)==i)cnt++;
  printf("%lld\n",(ll)*pw(,cnt-)%mod);
  return ;
}