Convolution and polynomial multiplication

https://www.mathworks.com/help/matlab/ref/conv.html?s_tid=gn_loc_drop

conv

Convolution and polynomial multiplication

Syntax

• w = conv(u,v)

  example

• w = conv(u,v,shape)

  example

Description

example

w = conv(u,v) returns the convolution of vectors u and v. If u and v are vectors of polynomial coefficients, convolving them is equivalent to multiplying the two polynomials.

example

w = conv(u,v,shape) returns a subsection of the convolution, as specified by shape. For example, conv(u,v,'same') returns only the central part of the convolution, the same size as u, and conv(u,v,'valid') returns only the part of the convolution computed without the zero-padded edges.

 

Examples

collapse all

Polynomial Multiplication via Convolution

Create vectors u and v containing the coefficients of the polynomials and .

u = [1 0 1];
v = [2 7];

Use convolution to multiply the polynomials.

w = conv(u,v)

w =

     2     7     2     7

w contains the polynomial coefficients for .

Vector Convolution

Create two vectors and convolve them.

u = [1 1 1];
v = [1 1 0 0 0 1 1];
w = conv(u,v)

w =

     1     2     2     1     0     1     2     2     1

The length of w is length(u)+length(v)-1, which in this example is 9.

 

Central Part of Convolution

Create two vectors. Find the central part of the convolution of u and v that is the same size as u.

u = [-1 2 3 -2 0 1 2];
v = [2 4 -1 1];
w = conv(u,v,'same')

w =

    15     5    -9     7     6     7    -1

w has a length of 7. The full convolution would be of length length(u)+length(v)-1, which in this example would be 10.

 

Input Arguments

u,v — Input vectors
vectors

Input vectors, specified as either row or column vectors. The
output vector is the same orientation as the first input argument, u.
The vectors u and v can be different
lengths or data types.

Data Types: double | single
Complex Number Support: Yes

shape — Subsection of convolution
'full' (default) | 'same' | 'valid'

Subsection of the convolution, specified as 'full', 'same',
or 'valid'.

'full'	Full convolution (default).
'same'	Central part of the convolution of the same size as u.
'valid'	Only those parts of the convolution that are computed without the zero-padded edges. Using this option, length(w) is max(length(u)-length(v)+1,0), except when length(v) is zero. If length(v) = 0, then length(w) = length(u).

Convolution

@向量的卷积 重叠面积

The convolution of two vectors, u and v, represents the area of overlap under the points as v slides across u. Algebraically, convolution is the same operation as multiplying polynomials whose coefficients are the elements of u and v.

Let m = length(u) and n = length(v) . Then w is the vector of length m+n-1 whose kth element is

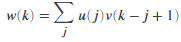
The sum is over all the values of j that lead to legal subscripts for u(j) and v(k-j+1), specifically j = max(1,k+1-n):1:min(k,m). When m = n, this gives

w(1) = u(1)*v(1)
w(2) = u(1)*v(2)+u(2)*v(1)
w(3) = u(1)*v(3)+u(2)*v(2)+u(3)*v(1)
...
w(n) = u(1)*v(n)+u(2)*v(n-1)+ ... +u(n)*v(1)
...
w(2*n-1) = u(n)*v(n)

https://www.zhihu.com/question/22298352?rf=21686447
“
：
卷积就是带权的积分
：
从概率论的角度来理解吧，举例为X Y 两组连续型随机变量，那么令Z＝X＋Y ，当X Y两组变量独立时，就能推导出卷积公式了，fz=fx*fy的意义就是在于两组变量叠加出来的概率密度，也就是算两信号X Y混叠起来的时候的响应
:
他的女儿是做环保的，有一次她接到一个项目，评估一个地区工厂化学药剂的污染（工厂会排放化学物质，化学物质又会挥发散去），然后建模狮告诉她药剂的残余量是个卷积。她不懂就去问她爸爸，prof就给她解释了。假设t时刻工厂化学药剂的排放量是f(t) mg，被排放的药物在排放后Δt时刻的残留比率是g(Δt) mg/mg；那么在u时刻，对于t时刻排放出来的药物，它们对应的Δt=u-t，于是u时刻化学药剂的总残余量就是∫f(t)g(u-t)dt，这就是卷积了。
”