Andrew Ng机器学习公开课笔记 -- Generalized Linear Models

网易公开课，第4课
notes，http://cs229.stanford.edu/notes/cs229-notes1.pdf

前面介绍一个线性回归问题，符合高斯分布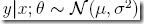
一个分类问题，logstic回归，符合伯努利分布

也发现他们有些相似的地方，其实这些方法都是一个更广泛的模型族的特例，这个模型族称为，广义线性模型（Generalized Linear Models，GLMs）

The exponential family

为了介绍GLMs，先需要介绍指数族分布（exponential family distributions）

参考，http://en.wikipedia.org/wiki/Exponential_family
The exponential families include many of the most common distributions, including the normal, exponential, gamma, chi-squared, beta, Dirichlet, Bernoulli, categorical, Poisson, Wishart, Inverse Wishart and many others.

这种分布族包含了很多常见的分布，其中包含了上面提到的高斯分布和伯努利分布
定义如下，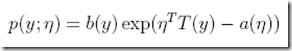

η is called the natural parameter (also called the canonical parameter) of the distribution
T(y) is the sufficient statistic (for the distributions we consider, it will often be the case that T(y) = y)
a(η) is the log partition function. The quantity 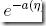essentially plays the role of a normalization constant, that makes sure the distribution p(y; η) sums/integrates over y to 1.

这个定义本身不那么好理解，不需要去理解它
当选定T，a和b这3个function时，就可以确定一种以η为参数的分布，比如以η为参数的高斯分布或伯努利分布
下面就看看从高斯分布或伯努利分布如何转换为指数族分布的形式，并且各自具体参数是什么？
伯努利分布的转换过程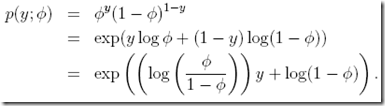

其中，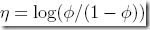
，即
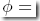
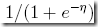
可以看到这就是logistic函数或sigmoid函数
之前只是单纯从分布图上说看上去使用logistic函数比线性更好
这里直接可以从伯努利分布推导出，需要使用logistic函数，参考后面的推导
另外的参数为，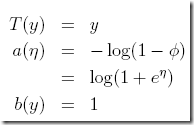

高斯分布的转换过程，
设 ，因为这个参数对回归结果没有影响，设什么都行，1更方便点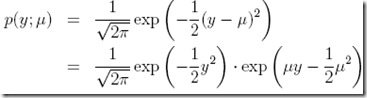

其中，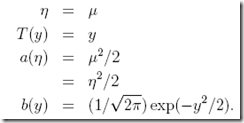
 

前面说了，指数族分布包含很多常用的分布，包含泊松分布。。。
这里以高斯和伯努利为例，当然其他的分布也可以完成这样的转换

 

Constructing GLMs

这里我们需要看看如何使用GLMs来解决分类和回归问题
如果要用GLMs来解决这个问题，需要基于下面的3个假设
To derive a GLM for this problem, we will make the following three assumptions about the conditional distribution of y given x and about our
model:
1. y | x; θ ∼ ExponentialFamily(η). I.e., given x and θ, the distribution of
y follows some exponential family distribution, with parameter η.
首先是符合ExponentialFamily分布，这是使用GLMs的前提

2. Given x, our goal is to predict the expected value of T(y) given x.
In most of our examples, we will have T(y) = y, so this means we would like the prediction h(x) output by our learned hypothesis h to satisfy h(x) = E[y|x]. (Note that this assumption is satisfied in the choices for h(x) for both logistic regression and linear regression. For instance, in logistic regression, we had h(x) = p(y = 1|x; θ) = 0 · p(y = 0|x; θ) + 1 · p(y = 1|x; θ) = E[y|x; θ].)
学习到的hypothesis h满足，h(x) = E[y|x]
可以看到前面在logistic回归中，我们选择的h(x)是满足这个假设的
3. The natural parameter η and the inputs x are related linearly: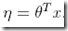
(Or, if η is vector-valued, then )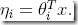
最后一个假设为，η和输入x满足线性关系
这条假设可以看成是一种”design choice”

基于上面3条假设，我们就可以GLMs学习算法来优雅的解决问题

下面看看如何基于上面假设来推导出线性回归和logistic回归的hypothesis h
前面碰到问题，都是直接先给出h，并没有说明为什么
这里可以通过GLMs，对特定问题和分布推导出h

线性回归
h(x) = E[y|x; θ]   //根据假设2
       = μ             //对于高斯分布，分布的期望为μ
       = η             //在由高斯分布转换到指数族分布时，得到μ=η
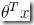       =         //根据假设3

Logistic回归
h(x) = E[y|x; θ]
       = φ
       =
       =
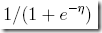
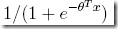
推导理由基本和上面的一样

Softmax回归
Logistic回归可以解决二元分类问题，但是对于多元分类，就需要使用Softmax回归来解决，比如对于邮件不是仅仅分为spam和not-spam，而是分为spam，personal，work
所以数据的分布也变成多项分布（multinomial distribution），是二项分布的推广

那么要解决这个问题，首先需要把多项分布转化为指数族分布
先声明一些假设，
假设有k个输出（k类），分到每类的概率为φ1, . . . , φk（对于二项分布为φ和1-φ）
φi = p(y = i; φ)
其实φk可以表示为，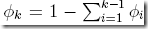
所以我们只需要定义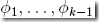 即可

另外这里需要定义T(y),虽然一般都是等于y，但这里T(y)为向量表示为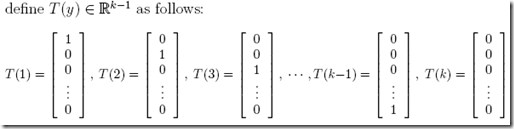

继续定义一个操作符，1{·}
(1{True} = 1, 1{False} = 0). For example, 1{2 = 3} = 0, and 1{3 =
5 − 2} = 1.
所以有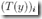， 可以表示为
，比较好理解，只有y=i时，才是1，其他都是0
进一步可以得到，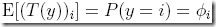
，因为求期望时，其他项都是×0，只会留下这项

下面给出多项分布的转换过程，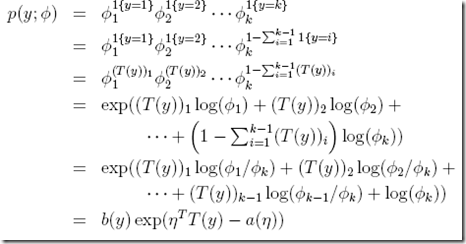

首先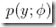为何等于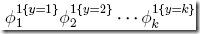
可以参考二项分布，这里只是简单的扩展，同样只会留下一项，其他项都为1
剩下的是基于前面假设的一些替换，
最终得到参数为，

 

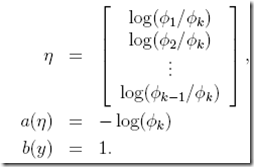
这里得到η和φ的关系，我们可以反推出，过程参考讲义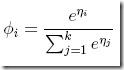
，根据GLMs第三假设，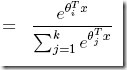
前面知道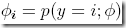 ，所以带入得到

到了这边，我们就可以用最大似然法来解决这个问题了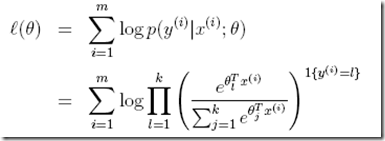
 
后面可以使用梯度上升或牛顿法来求解

同时根据GLMs第二假设，也可以给出hypothesis h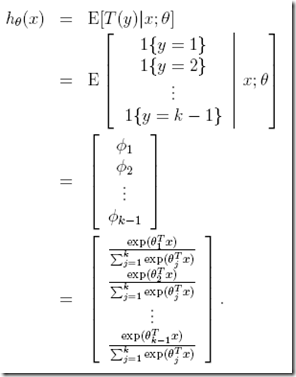
 

可见解决这类问题的关键就是推出p(y|x; θ)
因为有了这个，后面就可以使用最大似然法求解

对于logistic回归，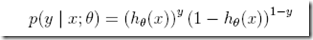

对于softmax回归，

而使用GLMs算法就可以直接的或间接的推导出p(y|x; θ)
首先通过统计分布函数可以得到P(y|φ), φ是参数，比如对于伯努利分布
可是为了拟合样本点，我们需要得到p(y|x; θ)，可是如果将φ转换成x
那么在GLMs中，通过转换，可以找到η和φ的关系
并且根据假设3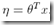，，所以通过GLMs我们就可以推导出p(y|x; θ)

我的理解，之所以成为广义线性模型
就是因为假设3，η和x是成线性关系的
虽然对于大部分的模型，都需要再进行一次指数族的转换才能得到H
特例就是线性回归，不需要做转换，H=η