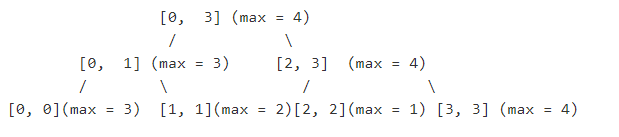lintcode-439-线段树的构造 II
439-线段树的构造 II
线段树是一棵二叉树,他的每个节点包含了两个额外的属性start和end用于表示该节点所代表的区间。start和end都是整数,并按照如下的方式赋值:
- 根节点的 start 和 end 由 build 方法所给出。
- 对于节点 A 的左儿子,有 start=A.left, end=(A.left + A.right) / 2。
- 对于节点 A 的右儿子,有 start=(A.left + A.right) / 2 + 1, end=A.right。
- 如果 start 等于 end, 那么该节点是叶子节点,不再有左右儿子。
对于给定数组设计一个build方法,构造出线段树
说明
wiki:
Segment Tree
Interval Tree样例
给出[3,2,1,4],线段树将被这样构造
标签
线段树
思路
自底向上构造线段树
code
/**
* Definition of SegmentTreeNode:
* class SegmentTreeNode {
* public:
* int start, end, max;
* SegmentTreeNode *left, *right;
* SegmentTreeNode(int start, int end, int max) {
* this->start = start;
* this->end = end;
* this->max = max;
* this->left = this->right = NULL;
* }
* }
*/
class Solution {
public:
/*
* @param A: a list of integer
* @return: The root of Segment Tree
*/
SegmentTreeNode * build(vector<int> A) {
// write your code here
if (A.size() <= 0) {
return nullptr;
}
return build(0, A.size() - 1, A);
}
SegmentTreeNode * build(int start, int end, vector<int> &nums) {
// write your code here
if (start > end) {
return nullptr;
}
SegmentTreeNode *root = new SegmentTreeNode(start, end, 0);
if (start != end) {
root->left = build(start, (start + end) / 2, nums);
root->right = build((start + end) / 2 + 1, end, nums);
root->max = max(root->left->max, root->right->max);
}
else {
root->max = nums[start];
}
return root;
}
};
lintcode-439-线段树的构造 II的更多相关文章
- lintcode:线段树的构造
线段树的构造 线段树是一棵二叉树,他的每个节点包含了两个额外的属性start和end用于表示该节点所代表的区间.start和end都是整数,并按照如下的方式赋值: 根节点的 start 和 end 由 ...
- 线段树(SegmentTree)基础模板
线段树模板题来源:https://www.lintcode.com/problem/segment-tree-build/description 201. 线段树的构造 /** * Definitio ...
- lintocde-247-线段树的查询 II
247-线段树的查询 II 对于一个数组,我们可以对其建立一棵 线段树, 每个结点存储一个额外的值 count 来代表这个结点所指代的数组区间内的元素个数. (数组中并不一定每个位置上都有元素) 实现 ...
- poj-----(2528)Mayor's posters(线段树区间更新及区间统计+离散化)
Mayor's posters Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 43507 Accepted: 12693 ...
- HDU 5820 (可持久化线段树)
Problem Lights (HDU 5820) 题目大意 在一个大小为50000*50000的矩形中,有n个路灯.(n<=500000) 询问是否每一对路灯之间存在一条道路,使得长度为|x1 ...
- HDU 4893 Wow! Such Sequence!(2014年多校联合 第三场 G)(线段树)
磨了一天的线段树,不能说完全搞清楚,只能说有一个大概的了解,靠着模板才把这道题A了,只能说太弱~~! 题意: 初始时有一字符串,全为0. 三种操作: 1 k d - add 把d加到第k个数上去2 ...
- 线段树(单标记+离散化+扫描线+双标记)+zkw线段树+权值线段树+主席树及一些例题
“队列进出图上的方向 线段树区间修改求出总量 可持久留下的迹象 我们 俯身欣赏” ----<膜你抄> 线段树很早就会写了,但一直没有总结,所以偶尔重写又会懵逼,所以还是要总结一下. ...
- poj2528线段树解题报告,离散化+线段树
题目网址:http://poj.org/problem?id=2528 题意: n(n<=10000)个人依次贴海报,给出每张海报所贴的范围li,ri(1<=li<=ri<=1 ...
- 线段树之成段更新( 需要用到延迟标记,简单来说就是每次更新的时候不要更新到底,用延迟标记使得更新延迟到下次需要更新or询问到的时候)
HDU 1698 链接: http://acm.hdu.edu.cn/showproblem.php?pid=1698 线段树功能:update:成段替换 (由于只query一次总区间,所以可以直 ...
随机推荐
- jqu
1 /*2 * 说明:3 * 本源代码的中文注释乃Auscarlin呕心沥血所作.旨在促进jQuery的传播以及向广大jQuery爱好者提供一个进阶4 *的途径,以让各位更加深入地了解jQuery,学 ...
- 大专生自学php到找到工作的前前后后
先做个自我介绍,我13年考上一所很烂专科民办的学校,学的是生物专业,具体的学校名称我就不说出来献丑了.13年我就辍学了,我在那样的学校,一年学费要1万多,但是根本没有人学习,我实在看不到希望,我就退学 ...
- Business Unit Helper
using System; using System.Linq; using Microsoft.Xrm.Sdk; using Microsoft.Crm.Sdk.Messages; using Sy ...
- python写爬虫时的编码问题解决方案
在使用Python写爬虫的时候,常常会遇到各种令人抓狂的编码错误问题.下面给出一些简单的解决编码错误问题的思路,希望对大家有所帮助. 首先,打开你要爬取的网站,右击查看源码,查看它指定的编码是什么,如 ...
- git——本地项目上传到git
1.对于github相信大家写自动化代码的人都不陌生,而且这也可以说是你进军自动化的一项必须解锁的技能,今天抽空开始整理笔记,顺便整理下github的基本使用,从本地上传代码托管: 一.从无到有:先注 ...
- (三)虚拟机与Linux新尝试——20155306白皎
(三)虚拟机与Linux新尝试--20155306白皎 一.关于虚拟机的安装 在选择虚拟机的类型和版本时,Ubuntu只有32位,没有64位 解决:通过百度,后来也发现同学们好多遇到了这个问题,因此通 ...
- 2017-2018-1 20155323《信息安全技术》实验二 Windows口令破解
2017-2018-1 20155323<信息安全技术>实验二 Windows口令破解 实验目的 了解Windows口令破解原理 对信息安全有直观感性认识 能够运用工具实现口令破解 系统环 ...
- 思维水题 poj1852
题目链接:http://poj.org/problem?id=1852 题意:木板长为n, 蚂蚁数量为k, 后面k个数,依次代表蚂蚁的位置, 当蚂蚁到达边界的时候会立马掉下,当两个蚂蚁相 ...
- OpenStack入门篇(一)之云计算的概念
1.云计算 云计算是一种按使用量付费的模式,这种模式提供可用的.便捷的.按需的网络访问, 进入可配置的计算资源共享池(资源包括网络,服务器,存储,应用软件,服务),这些资源能够被快速提供,只需投入很少 ...
- angular 缓存模板 ng-template $templateCache
由于浏览器加载html模板是异步加载的,如果加载大量的模板会拖慢网站的速度,这里有一个技巧,就是先缓存模板. 使用angular缓存模板主要有三种方法: 方法一:通过script标签引入 <sc ...