【SGU 390】Tickets (数位DP)
Description
Conductor is quite a boring profession, as all you have to do is just to sell tickets to the passengers. So no wonder that once upon a time in a faraway galaxy one conductor decided to diversify this occupation. Now this conductor sells several tickets at a time to each passenger. More precisely, he successively gives tickets to the passenger until the sum of the digits on all the tickets given becomes not less than some integer number k. Then this process repeats for the next passenger. Initially conductor has a tape of tickets numbered successively from l to r, inclusive. This way of tickets distribution is quite good, because passengers are glad to get several tickets when they pay only for one. But there is one disadvantage. Since each passenger gets several tickets, it is possible that conductor won't be able to serve all passengers. Your task is to help conductor in this difficult situation. You should calculate how many passengers is the conductor able to serve.
Input
Input file contains three integer numbers l, r and k (1 ≤ l ≤ r ≤ 10 18, 1 ≤ k ≤ 1000).Output
Output should contain exactly one number — the answer to the problem.Sample Input
【题意】
有一位售票员给乘客售票。对于每位乘客,他会卖出多张连续的票,直到已卖出的票的编号的数位之和不小于给定的正数 k。然后他会按照相同的规则给下一位乘客售票。初始时,售票员持有的票的编号是从 L 到 R 的连续整数。请你求出,售票员可以售票给多少位乘客。
【分析】
这题真难想啊,光是理解题解就理解了好久。。
这题跟前一题是相似的,都是划分区间,但是这题k很小,意味着区间很多,不能一个个区间跑的。这能模拟填数得到答案。模拟填数的话画一个树形图很重要。
一开始觉得画不画树都没什么关系,但是这题画了树真的好理解很多。因为这一题不能用ans[r]-ans[l],只能DP填l~r之间的数,而且要按从小到大的顺序,所以画树形图就很好看,可以拆成多个子树的并。
以下图为例,(假设是棵二叉树,好画点,做题的时候实际上是十叉的)。
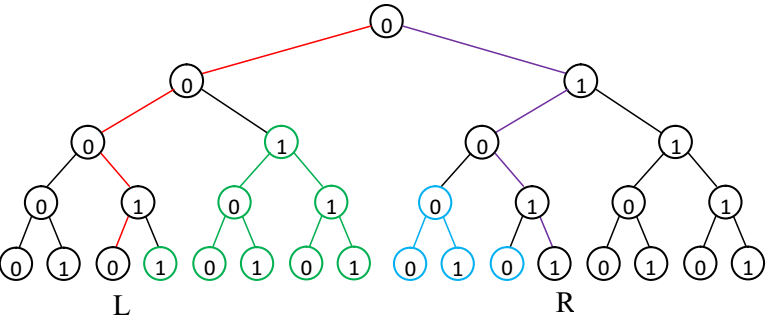
红色路径是L,绿色路径是R。我们填数实际上是从左边的绿色子树一直到右边的蓝色子树。
把原问题分解成多棵子树的子问题在并起来就好了。时间就会很快,是2*logn。
问题就是怎么把子树并起来,一开始会以为不可以,因为后子树的答案和前子树有关。但是我们注意到k很小,不妨记录一下前子树最后一个区间的空间,然后求后子树的答案。
然后这个子树其实是填数过程的后缀那部分的数,我们知道子树的位置所以也知道填数部分的前缀,这个对求子树答案是有影响的,我们子树上的每个数都要加上一个固定的数,所以也把他记录一下。即f[i][j][k]表示高度为i的子树,前子树最后一组剩余空间为j,每个数都要加上k时的答案(我们当作这棵子树的根权值为1,如果不为1而为i则把i加进k里面)。
f[[i][j][k]要记录分了多少组和最后一部分剩余多少,分别记为f[i][j][k].a,f[i][j][k].b
则f[i][j][k]=并(f[i][j][k],f[i-1][f[i][j][k].a][k+l]) (0<=l<=9)
并的话就很容易啦~~~
按顺序求答案就好啦~~
真是太厉害了,其实也不是很难,怎么我想不到,可能是因为之前都是做ans[r]-ans[l]的吧!!
代码如下:
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<queue>
#include<cmath>
using namespace std;
#define LL long long LL l,r;
int k,st;
int al[],ar[];
int hl[],hr[]; void init()
{
for(int i=;i<=;i++)
{
al[i]=(int)l%;l/=;
ar[i]=(int)r%;r/=;
}
for(st=;st>=;st--) if(al[st]!=ar[st]) break;
st++;
hl[]=hr[]=;
for(int i=;i>=;i--)
hl[i]=hl[i+]+al[i],hr[i]=hr[i+]+ar[i];
} struct node
{
LL sm;
int rm;
node ()
{
sm=-;
}
};
node f[][][];
node ans,rm; node get_ans(node x,node y)//combine
{
x.sm+=y.sm;
x.rm=y.rm;
return x;
} node get_f(int x,int y,int z)//x->height y->add z->room
{
if(f[x][y][z].sm!=-) return f[x][y][z];
node now;
if(x==)
{
now.sm=(y+z>=k)?:;
now.rm=(y+z>=k)?:y+z;
}
else
{
now=get_f(x-,y,z);
for(int i=;i<;i++)
{
now=get_ans(now,get_f(x-,y+i,now.rm));
}
}
return now;
} void ffind()
{
ans.sm=(hl[]>=k)?:;ans.rm=(hl[]>=k)?:hl[];
for(int i=;i<st;i++)
{
for(int j=al[i-]+;j<;j++)
{
ans=get_ans(ans,get_f(i-,hl[i]+j,ans.rm));
}
}
for(int i=al[st-]+;i<ar[st-];i++)
{
ans=get_ans(ans,get_f(st-,hl[st]+i,ans.rm));
}int i;
for(i=st-;i>=;i--)
{
for(int j=;j<ar[i-];j++)
{
ans=get_ans(ans,get_f(i-,hr[i]+j,ans.rm));
}
}
if(hr[]+ans.rm>=k) ans.sm++;
printf("%lld\n",ans.sm);
} int main()
{
freopen("a.in","r",stdin);
freopen("a.out","w",stdout);
scanf("%lld%lld%d",&l,&r,&k);
init();
ffind();
return ;
}
[SGU 390]
【其实我没有交,交不了...但是拍了感觉没什么问题..吧
还是放大神题解吧:

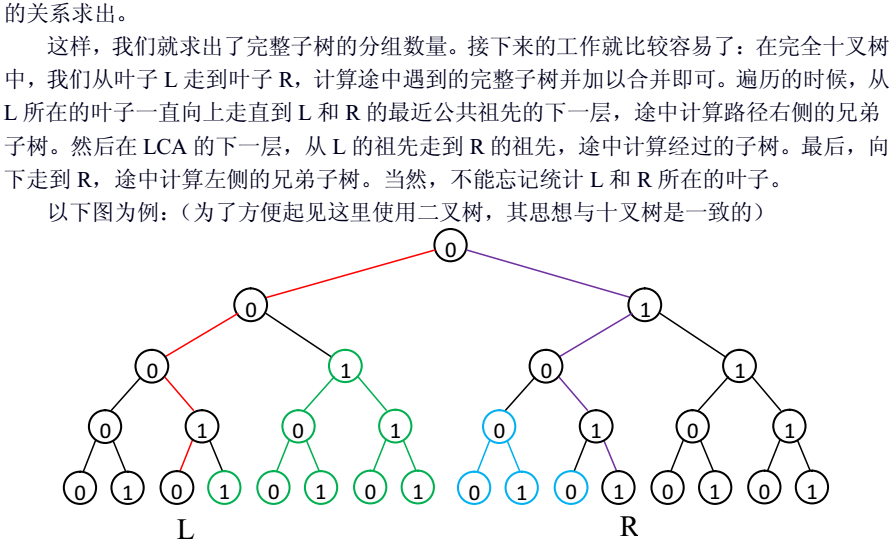

【SGU 390】Tickets (数位DP)的更多相关文章
- Codeforces Gym 100418J Lucky tickets 数位DP
Lucky ticketsTime Limit: 20 Sec Memory Limit: 256 MB 题目连接 http://acm.hust.edu.cn/vjudge/contest/view ...
- SGU 390-Tickets(数位dp)
题意:有标号l-r的票,要给路人发,当给的票的编号的各数位的总和(可能一个人多张票)不小k时,才开始发给下一个人,求能发多少人. 分析:这个题挺难想的,参考了一下题解,dp[i][sum][left] ...
- [DP]数位DP总结
数位DP总结 By Wine93 2013.7 1.学习链接 [数位DP] Step by Step http://blog.csdn.net/dslovemz/article/details/ ...
- Gym 100418J Lucky tickets(数位dp)
题意:给定一个n.求区间[1, n]之间的全部的a的个数.a满足: a能整除 把a表示自身二进制以后1的个数 思路:题意非常绕.... 数位dp,对于全部可能的1的个数我们都dfs一次 对于某一个可 ...
- SGU_390_Tickets(另类数位DP)
Tickets Time Limit : 1000/500ms (Java/Other) Memory Limit : 524288/262144K (Java/Other) Total Subm ...
- 【BZOJ1662】[Usaco2006 Nov]Round Numbers 圆环数 数位DP
[BZOJ1662][Usaco2006 Nov]Round Numbers 圆环数 Description 正如你所知,奶牛们没有手指以至于不能玩"石头剪刀布"来任意地决定例如谁 ...
- bzoj1026数位dp
基础的数位dp 但是ce了一发,(abs难道不是cmath里的吗?改成bits/stdc++.h就过了) #include <bits/stdc++.h> using namespace ...
- uva12063数位dp
辣鸡军训毁我青春!!! 因为在军训,导致很长时间都只能看书yy题目,而不能溜到机房鏼题 于是在猫大的帮助下我发现这道习题是数位dp 然后想起之前讲dp的时候一直在补作业所以没怎么写,然后就试了试 果然 ...
- HDU2089 不要62[数位DP]
不要62 Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submis ...
随机推荐
- Base64 encode/decode large file
转载:http://www.cnblogs.com/jzywh/archive/2008/04/20/base64_encode_large_file.html The class System.Co ...
- store procedure 翻页
store procedure 翻页例子 .turn page CREATE PROCEDURE pageTest --用于翻页的测试 --需要把排序字段放在第一列 ( )=null, --当前页面里 ...
- JDK版本过高,导致Eclipse报错
1.JDK版本如果比较高,而使用的eclipse版本比较低,导致在eclispe中不能识别而报错. 2.点击Attach Source添加rt.jar后,又出现如下错误 3.这样的错误就是由于ec ...
- 搭建Spring、Spring MVC、Mybatis和Freemarker
搭建Spring.Spring MVC.Mybatis和Freemarker 1.pom文件 <project xmlns="http://maven.apache.org/POM/4 ...
- IOS中的NSTimer定时器详解
/* 在IOS中有多种定时器,这里我对NSTimer定时器做了一个简单的介绍.如果你是小白,你可能会从这篇文章中学习到一些知识,如果你是大牛,请别吝啬你的评论,指出我的不足,你的质疑是对我最大的帮助. ...
- java新手笔记22 接口示例2
1.USB package com.yfs.javase; public interface USB { //定义规范 public void read(); public void write(); ...
- P1396 营救
P1396 营救 218 通过 571 提交 题目提供者yeszy 标签 二分 图论 并查集 福建省历届夏令营 难度 普及- 题目描述 "咚咚咚--""查水表!" ...
- CCPC网赛,HDU_5832 A water problem
Problem Description Two planets named Haha and Xixi in the universe and they were created ...
- HOW TO: Creating your MSI installer using Microsoft Visual Studio* 2008
Quote from: http://software.intel.com/en-us/articles/how-to-creating-your-msi-installer-using-visual ...
- HDU 5351 MZL's Border (规律,大数)
[HDU 5351 MZL's Border]题意 定义字符串$f_1=b,f_2=a,f_i=f_{i-1}f_{i-2}$. 对$f_n$的长度为$m$的前缀$s$, 求最大的$k$满足$s[1] ...
