BRISK: Binary Robust Invariant Scalable Keypoints

注意:本文含有一些数学公式，如果chrome不能看见公式的话请用IE打开网站

1.特征点提取

特征点提取有以下几个步骤:

a.尺度空间金字塔结构的构造

和SIFT类似，尺度空间金字塔是由不同的尺度构成，相互连续的两个尺度之间由Octave构成. 我们令t表示尺度，它们之间的计算关系如下:

$t({c_i}) = {2^i},t({d_i}) = {2^i} \cdot 1.5$

图像的大小为(width, height),举个例子:

width, 　　 height　　　　　　　　　　　　　scale1-octave1

(2/3)width, (2/3)height　　　　　　　　　　 scale1-octave2

(1/2)width, (1/2)height　　　　　　　　　　 scale2-octave1

(1/3)width, (1/3)height　　　　　　　　　　 scale2-octave2

(1/4)width, (1/4)height　　　　　　　　　　 scale3-octave1

(1/6)width, (1/6)height　　　　　　　　　　 scale3-octave2

其中 ${d_0}$ 由 ${c_0}$ 下采样得到. 不同octave之间的采样关系为2/3，不同尺度之间的采样关系为1/2. 关于构造的代码:

void BriskScaleSpace::constructPyramid(const cv::Mat& image){

    // set correct size:

    pyramid_.clear();

    // fill the pyramid:

    pyramid_.push_back(BriskLayer(image.clone()));

    if(layers_>){

        pyramid_.push_back(BriskLayer(pyramid_.back(),BriskLayer::CommonParams::TWOTHIRDSAMPLE));

    }

    const int octaves2=layers_;

    for(uint8_t i=; i<octaves2; i+=){

        pyramid_.push_back(BriskLayer(pyramid_[i-],BriskLayer::CommonParams::HALFSAMPLE));

        pyramid_.push_back(BriskLayer(pyramid_[i-],BriskLayer::CommonParams::HALFSAMPLE));

    }

}

b.通过阈值选取合适的关键点

关键点检测是通过FAST的算法进行的. FAST和AGAST在特征点检测中提供不同的模板。BRISK算法大部分使用FAST9-16提取特征点。首先，FAST9-16应用于每一个octave和每一层intra-octave，取相同的阈值T来分辨潜在的兴趣区域。然后，对兴趣区域中的点进行非极大值抑制：

1，问题点需要满足最大值条件，就是在同层中八邻域中的FAST score s最大。s定义为最大阈值是考虑到此点是图像角点。

2，同层和上下层的scores 应该都比此点的score s 小。检查等大小的方形patch内部：边长选择2像素。既然相邻层是不同离散化的，就需要在patch边缘进行插值。

3.由于确定一个特征点需要除本层以外的上下两层，但c0层是最底层，故需虚拟有一个d-1层，但这层不使用FAST9-16，而使用FAST5-8

非极大值抑制的代码:

 __inline__ bool BriskScaleSpace::isMax2D(const uint8_t layer,

         const int x_layer, const int y_layer){

     const cv::Mat& scores = pyramid_[layer].scores();

     const int scorescols = scores.cols;

     uchar* data=scores.data + y_layer*scorescols + x_layer;

     // decision tree:

     const uchar center = (*data);

     data--;

     const uchar s_10=*data;  //

     if(center<s_10) return false;

     data+=;

     const uchar s10=*data;    //

     if(center<s10) return false;

     data-=(scorescols+);

     const uchar s0_1=*data;    //

     if(center<s0_1) return false;

     data+=*scorescols;

     const uchar s01=*data;    //

     if(center<s01) return false;

     data--;

     const uchar s_11=*data;    //

     if(center<s_11) return false;

     data+=;

     const uchar s11=*data;    //

     if(center<s11) return false;

     data-=*scorescols;

     const uchar s1_1=*data;    //

     if(center<s1_1) return false;

     data-=;

     const uchar s_1_1=*data;//

     if(center<s_1_1) return false;

     /*8   3   7

       1   0   2

       5   4   6*/

     // reject neighbor maxima

     std::vector<int> delta;

     // put together a list of 2d-offsets to where the maximum is also reached

     if(center==s_1_1) { //

         delta.push_back(-);

         delta.push_back(-);

     }

     if(center==s0_1) {    //

         delta.push_back();

         delta.push_back(-);

     }

     if(center==s1_1) {    //

         delta.push_back();

         delta.push_back(-);

     }

     if(center==s_10) {    //

         delta.push_back(-);

         delta.push_back();

     }

     if(center==s10) {    //

         delta.push_back();

         delta.push_back();

     }

     if(center==s_11) {    //

         delta.push_back(-);

         delta.push_back();

     }

     if(center==s01) {    //

         delta.push_back();

         delta.push_back();

     }

     if(center==s11) {    //

         delta.push_back();

         delta.push_back();

     }

     const unsigned int deltasize=delta.size();

     if(deltasize!=){

         // in this case, we have to analyze the situation more carefully:

         // the values are gaussian blurred and then we really decide

         data=scores.data + y_layer*scorescols + x_layer;

         int smoothedcenter=*center+*(s_10+s10+s0_1+s01)+s_1_1+s1_1+s_11+s11;

         for(unsigned int i=; i<deltasize;i+=){

             //这里把左上角作为中心点进行平滑不知道是何意？

             data=scores.data + (y_layer-+delta[i+])*scorescols + x_layer+delta[i]-;

             int othercenter=*data;

             data++;

             othercenter+=*(*data);

             data++;

             othercenter+=*data;

             data+=scorescols;

             othercenter+=*(*data);

             data--;

             othercenter+=*(*data);

             data--;

             othercenter+=*(*data);

             data+=scorescols;

             othercenter+=*data;

             data++;

             othercenter+=*(*data);

             data++;

             othercenter+=*data;

             if(othercenter>smoothedcenter) return false;

         }

     }

     return true;

 }

c.去除不符合条件的关键点

2.特征点描述

和SIFT类似，尺度空间金字塔是由不同的尺度构成，相互连续的两个尺度之间由Octave构成. 我们令t表示尺度，它们之间的计算关系如下:

$t({c_i}) = {2^i},t({d_i}) = {2^i} \cdot 1.5$

其中 ${d_0}$ 由 ${c_0}$ 下采样得到. 不同octave之间的采样关系为2/3，不同尺度之间的采样关系为1/2.

b.通过阈值选取合适的关键点

1，问题点需要满足最大值条件，就是在同层中八邻域中的FAST score s最大。s定义为最大阈值是考虑到此点是图像角点。

3.由于确定一个特征点需要除本层以外的上下两层，但c0层是最底层，故需虚拟有一个d-1层，但这层不使用FAST9-16，而使用FAST5-8

c.去除不符合条件的关键点

2.特征点描述

BRISK算法在每个模式设置了60个点。

小的蓝色的圆表示在patch中的采样位置;大的红色虚线圆半径为 $\sigma$ 对应于用来平滑采样点亮度的高斯核的标准差。上图是尺度t=1的模式.

为了避免混叠效果，我们对在模式中的采样点Pi应用了高斯平滑. 标准差 ${\sigma _i}$ 正比于每个采样点对应于各自中心的距离.

然后对60个点两两选取组成点对。一共是(60-1)*60/2个点对。计算局部梯度:

$g({p_i},{p_j}) = ({p_j} - {p_i}) \cdot \frac{{I({p_j},{\sigma _j}) - ({p_i},{\sigma _i})}}{{{{\left\| {{p_j} - {p_i}} \right\|}^2}}}$

所有点对的集合为:

$A = \{ ({p_i},{p_j}) \in {\mathbb{R}^2} \times {\mathbb{R}^2}|i < N \wedge j < i \wedge i,j \in \mathbb{N}\}$

$S = \{ ({p_i},{p_j}) \in A|\left\| {{p_i} - {p_j}} \right\| < {\delta _{\max }}\} \subseteq A$

$L = \{ ({p_i},{p_j}) \in A|\left\| {{p_i} - {p_j}} \right\| > {\delta _{\min }}\} \subseteq A$

阈值距离的选取: ${\delta _{\max }} = 9.75t,{\delta _{\min }} = 13.67t$

迭代整个L上的点对，这样就可以估计出关键点k模式方向的整体特征:

$g = \left( \begin{array}{l} {g_x}\\ {g_y} \end{array} \right) = \frac{1}{L} \cdot \sum\limits_{({p_i},{p_j}) \in L} {g({p_i},{p_j})}$

长距离的点对都参与了运算，基于本地梯度互相抵消的假说，所以全局梯度的计算是不必要的。这一点同时也被距离变量阈值 ${\delta _{\min }}$ 的实验确认了

3.创建描述子

对于旋转和尺度归一化的描述子的建立，BRISK使用了关键点周围的抽样点旋转 $\alpha = \arctan 2({g_x},{g_y})$ 角度作为模式。和BRIEF类似，BIRSK的描述子也是一个包含512个比特位的向量，每个描述子由短距离点对 $(p_j^\alpha ,p_i^\alpha ) \in S$ 两两进行比较产生的，上标alpha表示旋转的模式。

$b = \left\langle \begin{array}{l} 1,I(p_j^\alpha ,{\sigma _j}) > (p_i^\alpha ,{\sigma _i})\\ 0,otherwise \end{array} \right.,\forall (p_j^\alpha ,p_i^\alpha ) \in S$

与BRIEF不同的地方是，BRIEF只是进行亮度比较，除了预设尺度和预先对样本模式的旋转之外，BRISK和BRIEF有着根本的区别:

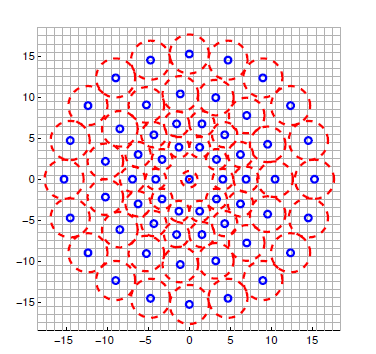
a.BRISK使用固定的样本模式点，而且是以R为半径围绕关键点周围的圆进行均匀取样。因此特定的高斯核平滑不会突然地扭曲亮度内容的信息(模糊邻近的两个采样点的亮度，从而保证亮度平滑过渡)
b.与两两组成的点对相比，BRISK显著的减少了采样点的数量(例如，单个的样本点参与了更多的比较)，限制了亮度查找表的复杂度
c.这里的比较是受到空间的限制的，所以亮度的改变仅仅只是需要局部一致性就可以了。

程序中用到的算法:

1.利用least square进行曲线拟合中的参数计算

二次曲线的标准公式如下：

$y = a + bx + c{x^2}$

给定数据:

$({x_1},{y_1}),({x_2},{y_2}),({x_3},{y_3}),.......,({x_n},{y_n})$

令 ${y_\lambda }$ 函数在 ${x_1}$ 的理论值，然后有: $e = {y_1} - {y_\lambda }$

$\begin{array}{l} {e_1} = {y_1} - (a + b{x_1} + cx_1^2)\\ e_1^2 = {({y_1} - a - b{x_1} - cx_1^2)^2} \end{array}$

根据最小二乘定理，当下列偏导数等于0时使得S最小.

$\frac{{\partial S}}{{\partial u}} = 0,\frac{{\partial S}}{{\partial b}} = 0,and\frac{{\partial S}}{{\partial c}} = 0$

用方程组的形式表示出来:

$\sum y = na + b\sum x + c\sum {{x^2}}$

$\sum {xy} = a\sum x + b{\sum x ^2} + c\sum {{x^3}}$

$\sum {{x^2}y} = a{\sum x ^2} + b{\sum x ^3} + c\sum {{x^4}}$

这里有个比较疑惑的地方, refine1D, refine1D_1, refine1D_2这三个函数的矩阵是选取什么样的尺度初值算出来的？有知道朋友可以说说。

2.least square二次曲面拟合的参数计算

二次曲面的标准公式如下:

$z = f(x,y) = {c_1}{x^2} + {c_2}xy + {c_3}{y^2} + {c_4}x + {c_5}y + {c_6} = C \cdot Q(x,y)$

这里 $C = ({c_1},{c_2},{c_3},{c_4},{c_5},{c_6}),Q(x,y) = ({x^2},xy,{y^2},x,y,1)$ ，选择C使得平方误差最小：

$E(C) = \sum\limits_{i = 1}^m {{{(C \cdot {Q_i} - {z_i})}^2}}$ ，其中 ${Q_i} = Q({x_i},{y_i})$

当梯度E为0向量的时候上式取得最小值。

$\nabla E = 2\sum\limits_{i = 1}^m {(C \cdot {Q_i} - {z_i}){Q_i} = 0}$

也可以写成含有6个未知变量的6个方程组的形式:

$(\sum\limits_{i = 1}^m {{Q_i}{Q_i}^T} )C = \sum\limits_{i = 1}^m {{z_i}{Q_i}}$

${Q_i}Q_i^T$ 是6X1的矩阵 ${Q_i}$ 和1X6的矩阵 $Q_i^T$ 的乘积.

6x6的矩阵

$A = (\sum\limits_{i = 1}^m {{Q_i}{Q_i}^T} )$ ，

6x1向量

$B = \sum\limits_{i = 1}^m {{z_i}{Q_i}}$

所以AC=B.

单个元素的例子:

$s({x^3}y) = \sum\limits_{i = 1}^m {x_i^3{y_i}}$

3.平滑函数

曲面拟合采用的是线性曲面拟合

注意，程序中的积分路线是45度角度路径进行积分的。

4.曲面插值

smoothedIntensity，BriskLayer::value这两个函数中使用了曲面插值算法。

5.重采样

重采样使用SSE指令对采样进行加速。

reference:

1.<Curve Fitting and Solution of Equation>

2.<Least Squares Fitting of Data> David Eberly

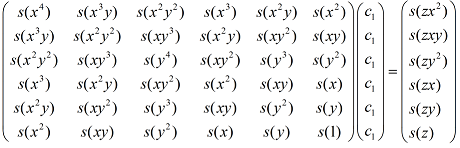
3.<BRISK: Binary Robust Invariant Scalable Keypoints> Stefan Leutenegger, Margarita Chli and Roland Y. Siegwart

BRISK: Binary Robust Invariant Scalable Keypoints的更多相关文章

【特征匹配】BRISK原文翻译
原文:Stefan Leutenegger, Margarita Chli et al.<BRISK: Binary Robust Invariant Scalable Keypoints> ...
opencv::Brisk检测与匹配
Brisk(Binary Robust Invariant Scalable Keypoints)特征介绍构建尺度空间特征点检测 FAST9-16寻找特征点特征点定位关键点描述子
Computer Vision_33_SIFT：TILDE: A Temporally Invariant Learned DEtector——2014
此部分是计算机视觉部分,主要侧重在底层特征提取,视频分析,跟踪,目标检测和识别方面等方面.对于自己不太熟悉的领域比如摄像机标定和立体视觉,仅仅列出上google上引用次数比较多的文献.有一些刚刚出版的 ...
【特征检测】BRISK特征提取算法
[特征检测]BRISK特征提取算法原创hujingshuang 发布于2015-07-24 22:59:21 阅读数 17840 收藏展开简介 BRISK算法是2011年ICCV上< ...
opencv中的SIFT,SURF,ORB,FAST 特征描叙算子比较
opencv中的SIFT,SURF,ORB,FAST 特征描叙算子比较参考: http://wenku.baidu.com/link?url=1aDYAJBCrrK-uk2w3sSNai7h52x_ ...
（1）RGB-D SLAM系列- 工具篇（硬件+关键技术）
/*************************************************************************************************** ...
OpenCV特征点提取----Fast特征
1.FAST(featuresfrom accelerated segment test)算法 http://blog.csdn.net/yang_xian521/article/details/74 ...
图像局部显著性—点特征（SIFT为例）
基于古老的Marr视觉理论,视觉识别和场景重建的基础即第一阶段为局部显著性探测.探测到的主要特征为直觉上可刺激底层视觉的局部显著性--特征点.特征线.特征块. SalientDetection 已经好 ...
Computer Vision_33_SIFT：Remote Sensing Image Registration With Modified SIFT and Enhanced Feature Matching——2017
此部分是计算机视觉部分,主要侧重在底层特征提取,视频分析,跟踪,目标检测和识别方面等方面.对于自己不太熟悉的领域比如摄像机标定和立体视觉,仅仅列出上google上引用次数比较多的文献.有一些刚刚出版的 ...

随机推荐

Java Swing 第03记布局管理器
几种Swing常用的布局管理器 BorderLaout 它将容器分为5个部分,即东.南.西.北.中,每一个区域可以容纳一个组件,使用的时候也是通过BorderLayout中5个方位常量来确定组件所在的 ...
第10章嵌入式Linux的调试技术
printk函数运行在内核空间,printf函数运行在用户空间.也就是说像Linux驱动这样的Linux内核程序只能使用printk函数输出调试信息.printk函数在控制台(也称终端)显示消息是通过 ...
javaweb常见问题解决
问题一.如果是在导入的项目的情况下,多数情况下就是jdk版本与项目的jdk版本不匹配, 解决方法: (1)右击工程->Build Path->Configure Build Path-&g ...
jquery点赞和取消点赞插件
<script> /* @author:Romey * 动态点赞 * 此效果包含css3,部分浏览器不兼容(如:IE10以下的版本) */ $(function(){ $("#p ...
ThinkPHP 自动验证相关注意
1.假如加入了表单令牌的话,表单的各种名与对应Model字段一致,不然报坑爹的令牌错误. 2.假如加入了表单令牌的话,Create只能采用默认的POST数据创建数据对象,不然又是坑爹的令牌错误. 3. ...
IOS－当遇到tableView整体上移时的解决方案
方案一在使用了navigationController后,当界面进行跳转往返后,时而会出现tableView或collectionView上移的情况,通常会自动上移64个像素,那么这种情况,我们可以关 ...
SILVERLIGHT 应急卫生模拟演练项目之loading界面实现
第一次在博客园写文章俺是菜鸟有不足之处还请大佬们多多指教第一次也不知道该写啥俺就拿自己最近做的一个项目来细说吧俺们公司是做医疗卫生方面的其中有一块涉及到应急卫生模拟演练方面这块分到我 ...
vconfig使用帮助
====================================================== VCONFIG(8) ...
【Android Studio快捷键】之代码提示
接下来说如何设置代码自动提示,如图: 图上内容比较多,我直接按区域划分成6块区域来说吧: 区域1:这个选项是关于提示的时候如何进行匹配,即按照什么条件来进行提示内容的搜索. All:选择这个的话,意思 ...
Autofac 同时支持MVC 与Webapi
1.引用 using Autofac; using Autofac.Integration.Mvc; using Autofac.Integration.WebApi; 2.在Global中的Appl ...

BRISK: Binary Robust Invariant Scalable Keypoints

BRISK: Binary Robust Invariant Scalable Keypoints的更多相关文章

随机推荐

热门专题