一道很经典的 BFS 题

想认真的写篇题解。

题目来自：https://www.luogu.org/problemnew/show/P1126

题目描述

机器人移动学会（RMI）现在正尝试用机器人搬运物品。机器人的形状是一个直径$1.6米的球。在试验阶段，机器人被用于在一个储藏室中搬运货物。储藏室是一个N×M的网格，有些格子为不可移动的障碍。机器人的中心总是在格点上，当然，机器人必须在最短的时间内把物品搬运到指定的地方。机器人接受的指令有：向前移动1步（Creep）；向前移动2步（Walk）；向前移动3步（Run）；向左转（Left）；向右转（Right）。每个指令所需要的时间为1秒。请你计算一下机器人完成任务所需的最少时间。

输入

第一行为两个正整数N,M(N,M≤50)，下面N行是储藏室的构造，0表示无障碍，1表示有障碍，数字之间用一个空格隔开。接着一行有4个整数和1个大写字母，分别为起始点和目标点左上角网格的行与列，起始时的面对方向（东E，南S，西W，北N），数与数，数与字母之间均用一个空格隔开。终点的面向方向是任意的。

输出

一个整数，表示机器人完成任务所需的最少时间。如果无法到达，输出-1。

图例

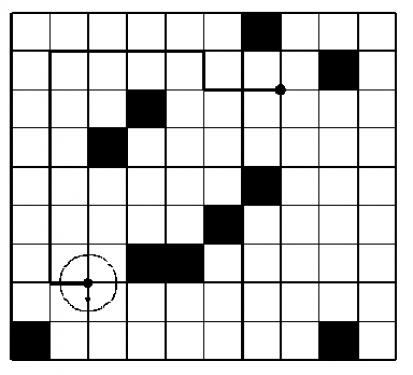
分析

以前在刷刘汝佳的紫书《算法竞赛入门经典》时做过这道题，现在又再次遇到，幸不汝（辱）命，一次就过了。

BFS 性质

我们都知道，BFS 具有从起点到目标节点（或状态）路径最短的特性，但是使用 BSF 这一特性时需要注意，只有当所有的边权重相同（一般为1）时，它才具有此性质，边权不等时不具有。BFS 每次从一个节点只经历一次转移，当求单纯的求距离时可以认为每次转移的边权为一，转移次数最少的路径一定是距离最短的。我们可以用两张图来直观的表现这个特性：

在图上：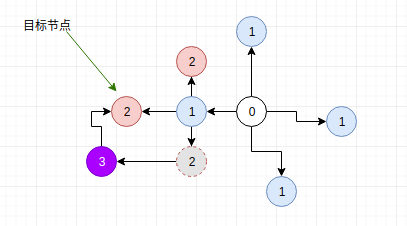

初始节点为 0，每次从一个节点向四周节点扩散，访问所有距离为一（相邻，经过一次状态转换）的节点。

第一次扩散访问了所有蓝色节点，并没有找到目标节点，继续扩散。第二次扩散访问了两个粉色节点，虚线节点并没有被访问。因为在扩散到左边的粉色节点时，我们已经找到了目标节点。那么不去搜索第三个粉色节点（虚线）节点不会丢解吗？在图中我们也确实能看到，虚线节点在经历一次扩散后，到达紫色节点，紫色节点再扩散一次，也可到达目标节点。不过，这个选择无论是从上述图片还是从我的描述文字来看，他的距离都不短。那么为什么会这样呢？我说一下我个人的理解。看下面一幅图：

在树上：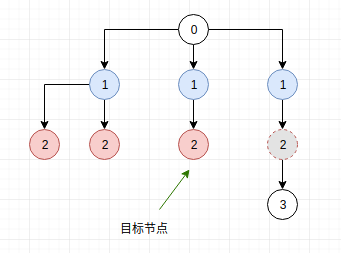

在树上的 BFS 被称为层次遍历。他的工作原理就如其名，每次访问一层的节点，同一层的节点有一个特点就是，他们的层数是相同的，也即到根节点的距离。当扩散到第三层时，（从左向右）第三个粉色节点作为目标节点被发现，此时我们可以对比三种情况：

由于第三个粉色节点为第一个目标节点，所以所有该节点左侧同层节点都不是目标节点，并且从这些节点继续扩散出的节点的层数（即到根节点的距离）一定大于第三个粉色节点到根节点的距离。
对于第三个粉色节点，也即我们的第一个目标节点（为什么强调 “第一个” 因为可能有不止一个目标节点，即多个解），由他扩散而出的子节点的距离一定大于这个节点。
对于虚线节点，由于他是不是目标节点，在未访问到时未知，而他的性质是和第一种情况相似的，所以去访问并扩散虚线节点我们能得到的结果是他的距离

大于等于 第三个粉色节点

由此，可以得出如果只有一个解，那么第一次被发现的目标节点即第三个粉色节点一定是距离根节点最近的。

在图上也可以类比层的概念，得出相同的结论。

解题思路

BFS 的性质讨论完，再来具体考虑这道题。这道题应该能明显看出来，是在图上寻找最短路的问题。不过首先需要对数据进行一些分析处理，才能更好的应用 BFS。此题唯一有些麻烦的就是，机器人具有半径，将每个格子单独处理不方便。由给出的图例可以发现，机器人一定会占据四个格子的空间，而一旦一个格子障碍物出现，那么这个障碍物格子所在的四个四方格上的中心格点机器人都不能走（机器人只走格点）。

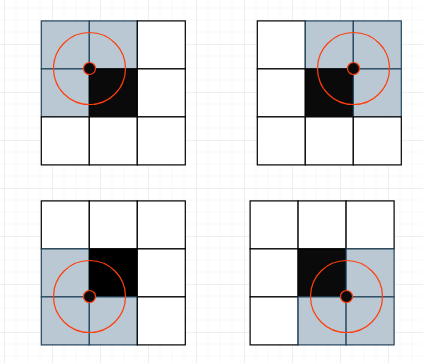
所以在读完输入键一个图后，可以再创建一个简化版的图，mini map。它将原图中每四个格点当做一个点，而机器人只走这四个格子的中心，一旦一个四方格中有一个障碍，那么这个四方格认为不可走。这样一来机器人移动、机器人半径、单个方格障碍物问题就简化成了最常见的情况：在一个图上的点避开障碍物到达另一个点的最短路。（这中简化和机器人在原图上的移动是等价的，可以模拟一下）。

以下是这部分处理代码：

	for(int i = 0; i < n; ++i) {

		for(int j = 0; j < m; ++j) {

			cin >> graph[i][j];

		}

	}

	int p = 0,q = 0;

	for(int i = 0; i < n-1; ++i) {

		q = 0;

		for(int j = 0; j < m-1; ++j) {

			if(graph[i][j] || graph[i][j+1] || graph[i+1][j] || graph[i+1][j+1])

				mini[p][q] = 1;//标记为障碍，否则为 0 表示可达

			q++;

		}

		p++;

	}

建出了图，现在考虑状态的转移。此题中，每个节点可以有三种转移情况，向左转，向右转，移动。

每种情况耗时为 1（可以认为是距离，权重）。关于转向问题，可以定义一个方向数组，按顺时针顺序给出北东南西，然后无论朝向那个方位，向左转就是数组索引减一，向右转就是加一，检索方向数组获得新的方位。完成一次转向后，就完成了一次状态转移，将新的节点入队列，这个新的节点在下一次被取出考虑进行转移状态时，他的当前方向就是移动的方向。

宏和数据结构：

#define MAX 50

#define DIR 4

#define N 0

#define E 1

#define S 2

#define W 3

struct Node {

	int x,y;

	int step = 0;

	int d;

	Node (int x,int y,int step,int dir) {

		this->x = x,this->y = y,this->step = step,this->d = dir;

	}

	// Node () {}

	// int pre = 0;

	// int loc = 0;

};

int graph[MAX + 1][MAX + 1];

int mini[MAX + 1][MAX + 1];		//mini graph

int vis[MAX + 1][MAX + 1][DIR];

//			N  E  S  W

int dx[] = {-1,0, 1, 0};

int dy[] = {0, 1, 0,-1};

int n,m;

BFS 代码：



Node bfs(int sx,int sy,int tx,int ty,int dir) {

	queue<Node> q;

	Node start = Node(sx,sy,0,dir);

	q.push(start);

	// path[pi++] = start;

	vis[sx][sy][dir] = 1;

	while(!q.empty()) {

		Node u = q.front();

		q.pop();

		if(u.x == tx && u.y == ty) return u;

		//尝试向左转

		if(!vis[u.x][u.y][(u.d-1+DIR)%DIR]) {

			vis[u.x][u.y][(u.d-1+DIR)%DIR] = 1;

			Node nu = Node(u.x,u.y,u.step+1,(u.d-1+DIR)%DIR);

			// nu.pre = u.loc;		//记录路径信息

			// nu.loc = pi;

			// path[pi++] = nu;

			q.push(nu);

		}

		//尝试向右转

		if(!vis[u.x][u.y][(u.d+1)%DIR]) {

			vis[u.x][u.y][(u.d+1)%DIR] = 1;

			Node nu = Node(u.x,u.y,u.step+1,(u.d+1)%DIR);

			// nu.pre = u.loc;

			// nu.loc = pi;

			// path[pi++] = nu;

			q.push(nu);

		}

		//尝试移动 creep，walk，run

		for(int i = 1; i <= 3; ++i) {

			Node nu = Node(u.x,u.y,u.step+1,u.d);

			//判断是是否有障碍物。只要有一个，就不必移动了。

			bool isok = true;

			for(int j = 0; j < i; ++j) {

				if(mini[nu.x+dx[u.d]*j][nu.y+dy[u.d]*j])

					{ isok = false; break; }

			}

			if(isok == false) break;

			nu.x += dx[u.d] * i;

			nu.y += dy[u.d] * i;

			if(inrange(nu) && !vis[nu.x][nu.y][nu.d]) {

				vis[nu.x][nu.y][nu.d] = 1;

				// nu.pre = u.loc;

				// nu.loc = pi;

				// path[pi++] = nu;

				q.push(nu);

			}

		}

	}

	return Node(-1,-1,-1,-1);

}

其中注释代码是用来记录最短路的路径信息。在这里是我用来测试程序的。

在调试的时候遇到一个 bug 花了我几个小时，机器人移动方式有 creep，walk，run，分别移动 1 、2 、3 步，在移动步数大于 1 时，不能只判断目标节点是否是障碍物，而要判断每一步是否有障碍物。

完整程序：

#include <iostream>

#include <algorithm>

#include <cstring>

#include <stdlib.h>

#include <memory.h>

#include <queue>

using namespace std;

#define MAX 50

#define DIR 4

#define N 0

#define E 1

#define S 2

#define W 3

struct Node {

	int x,y;

	int step = 0;

	int d;

	Node (int x,int y,int step,int dir) {

		this->x = x,this->y = y,this->step = step,this->d = dir;

	}

	// Node () {}

	// int pre = 0;

	// int loc = 0;

};

int graph[MAX + 1][MAX + 1];

int mini[MAX + 1][MAX + 1];		//mini graph

int vis[MAX + 1][MAX + 1][DIR];

//			N  E  S  W

int dx[] = {-1,0, 1, 0};

int dy[] = {0, 1, 0,-1};

int n,m;

// Node path[MAX * MAX + 1];

// int pi = 0;

bool inrange(Node nd) {

	return nd.x >= 0 && nd.x <= n-2 && nd.y >= 0 && nd.y <= m-2;

}

Node bfs(int sx,int sy,int tx,int ty,int dir) {

	queue<Node> q;

	Node start = Node(sx,sy,0,dir);

	q.push(start);

	// path[pi++] = start;

	vis[sx][sy][dir] = 1;

	while(!q.empty()) {

		Node u = q.front();

		q.pop();

		if(u.x == tx && u.y == ty) return u;

		//尝试向左转

		if(!vis[u.x][u.y][(u.d-1+DIR)%DIR]) {

			vis[u.x][u.y][(u.d-1+DIR)%DIR] = 1;

			Node nu = Node(u.x,u.y,u.step+1,(u.d-1+DIR)%DIR);

			// nu.pre = u.loc;		//记录路径信息

			// nu.loc = pi;

			// path[pi++] = nu;

			q.push(nu);

		}

		//尝试向右转

		if(!vis[u.x][u.y][(u.d+1)%DIR]) {

			vis[u.x][u.y][(u.d+1)%DIR] = 1;

			Node nu = Node(u.x,u.y,u.step+1,(u.d+1)%DIR);

			// nu.pre = u.loc;

			// nu.loc = pi;

			// path[pi++] = nu;

			q.push(nu);

		}

		//尝试移动 creep，walk，run

		for(int i = 1; i <= 3; ++i) {

			Node nu = Node(u.x,u.y,u.step+1,u.d);

			////判断是是否有障碍物。只要有一个，就不必移动了。

			bool isok = true;

			for(int j = 1; j <= i; ++j) {

				if(mini[nu.x+dx[u.d]*j][nu.y+dy[u.d]*j])

					{ isok = false; break; }

			}

			if(isok == false) break;

			nu.x += dx[u.d] * i;

			nu.y += dy[u.d] * i;

			if(inrange(nu) && !vis[nu.x][nu.y][nu.d]) {

				vis[nu.x][nu.y][nu.d] = 1;

				// nu.pre = u.loc;

				// nu.loc = pi;

				// path[pi++] = nu;

				q.push(nu);

			}

		}

	}

	return Node(-1,-1,-1,-1);

}

int main(int argc, char const *argv[])

{

	freopen("/home/skipper/Documents/code/刷题/洛谷 OJ/重启/in.txt","r",stdin);

	int sx,sy,tx,ty;

	char dir;

	cin >> n >> m;

	for(int i = 0; i < n; ++i) {

		for(int j = 0; j < m; ++j) {

			cin >> graph[i][j];

		}

	}

	int p = 0,q = 0;

	for(int i = 0; i < n-1; ++i) {

		q = 0;

		for(int j = 0; j < m-1; ++j) {

			if(graph[i][j] || graph[i][j+1] || graph[i+1][j] || graph[i+1][j+1])

				mini[p][q] = 1;

			q++;

		}

		p++;

	}

	int d;

	cin >> sx >> sy >> tx >> ty >> dir;

	switch(dir) {

		case 'S': d = S;break;

		case 'N': d = N;break;

		case 'E': d = E;break;

		case 'W': d = W;break;

	};

	//test 查看 mini map

	// for(int i = 0; i < p; ++i) {

	// 	for(int j = 0; j < q; ++j) {

	// 		cout << mini[i][j] << " ";

	// 	}

	// 	cout << endl;

	// }

	Node res = bfs(sx-1,sy-1,tx-1,ty-1,d);

	//输出路径

	// int pp = res.loc;

	// do {

	// 	cout << path[pp].x << "," << path[pp].y << endl;

	// 	pp = path[pp].pre;

	// }while(pp);

	cout << res.step << endl;

	return 0;

}

如有错误，欢迎指正评论。

作者：Skipper

出处：https://www.cnblogs.com/backwords/p/10542486.html

本博客中未标明转载的文章归作者 Skipper 和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。