机器学习基石12-Nonlinear Transformation
注:
文章中所有的图片均来自台湾大学林轩田《机器学习基石》课程。
笔记原作者:红色石头
微信公众号:AI有道
上一节课介绍了分类问题的三种线性模型,可以用来解决binary classification和multiclass classification问题。本节课主要介绍非线性的模型来解决分类问题。
一、Quadratic Hypothesis
之前介绍的线性模型,在2D平面上是一条直线,在3D空间中是一个平面。数学上,我们用线性得分函数\(s\)来表示:\(s=w^Tx\) 。其中,\(x\)为特征值向量,\(w\)为权重,\(s\)是线性的。
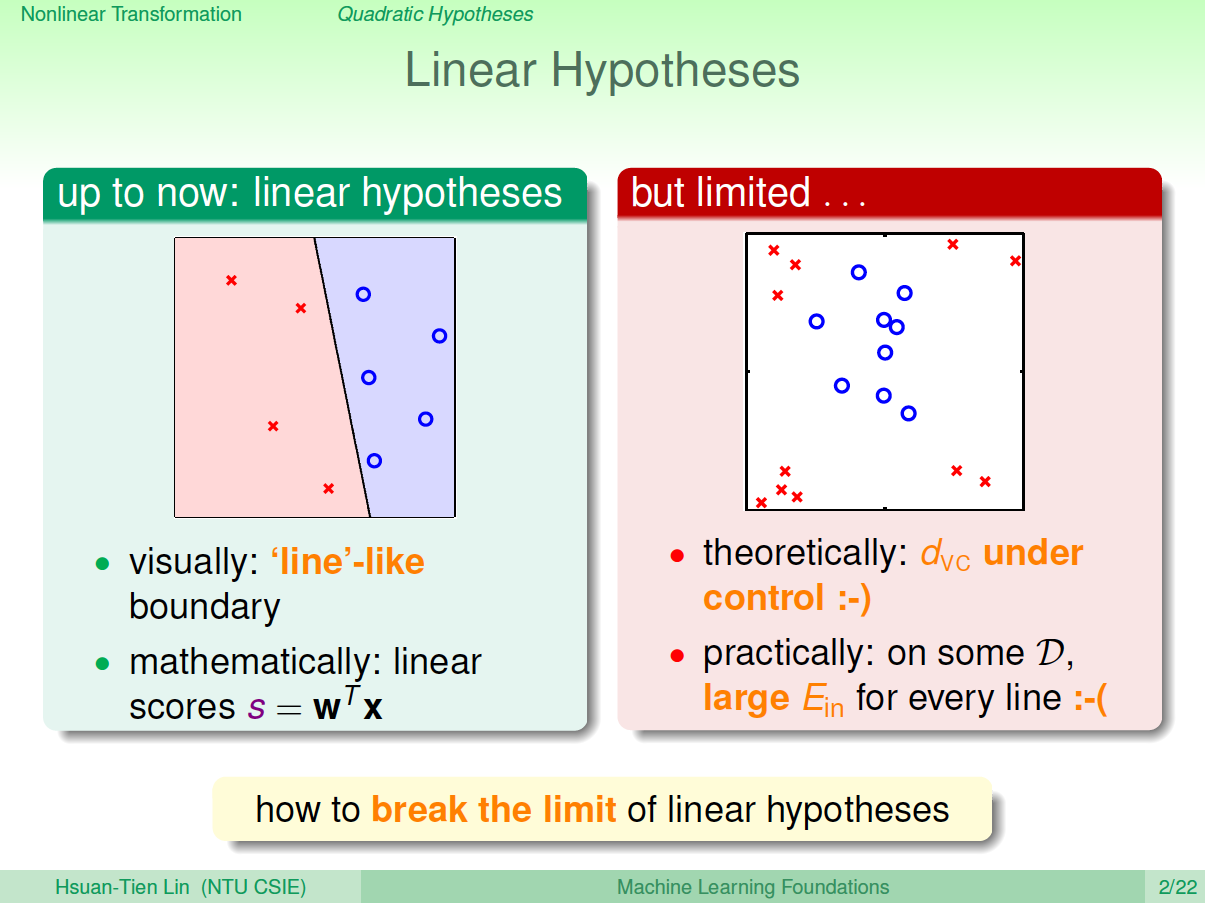
线性模型的优点就是,它的VC Dimension比较小,保证了\(E_{in}\approx E_{out}\)。但是缺点也很明显,对某些非线性问题,可能会造成\(E_{in}\)很大,虽然\(E_{in}\approx E_{out}\),但是\(E_{out}\)也很大,分类效果不佳。
为了解决线性模型的缺点,我们可以使用非线性模型来进行分类。例如数据集D不是线性可分的,而是圆形可分的,圆形内部是正类,外面是负类。假设它的hypotheses可以写成:\[h_{SEP}(x)=sign(-x^2_1-x^2_2+0.6)\]基于这种非线性思想,之前讨论的PLA、Regression问题都可以有非线性的形式进行求解。

下面介绍如何设计这些非线性模型的演算法。还是上面介绍的平面圆形分类例子,它的\(h(x)\)的权重\(w_0=0.6\), \(w_1-1=\), \(w_2=-1\),但是\(h(x)\)的特征不是线性模型的\((1,x_1,x_2)\),而是\((1,x^2_1,x^2_2)\)。令\(z_0=1\), \(z_1=x^2_1\), \(z_2=x^2_2\),那么\(h(x)\)变成:\[h(x)=sign(\tilde{w}_0 z_0+\tilde{w}_1 z_1+\tilde{w}_2z_2)=sign(0.6z_0-1z_1-1z_2)=sign(\tilde{w}^Tz)\] 这种\(x_n\)到\(z_n\)的转换可以看成是\(x\)空间的点映射到\(z\)空间中去,而在\(z\)域中,可以用一条直线进行分类,也就是从\(x\)空间的圆形可分映射到\(z\)空间的线性可分。\(z\)域中的直线对应于\(x\)域中的圆形。因此,我们把这个过程称之为特征转换(Feature Transform)。通过这种特征转换,可以将非线性模型转换为另一个域中的线性模型。
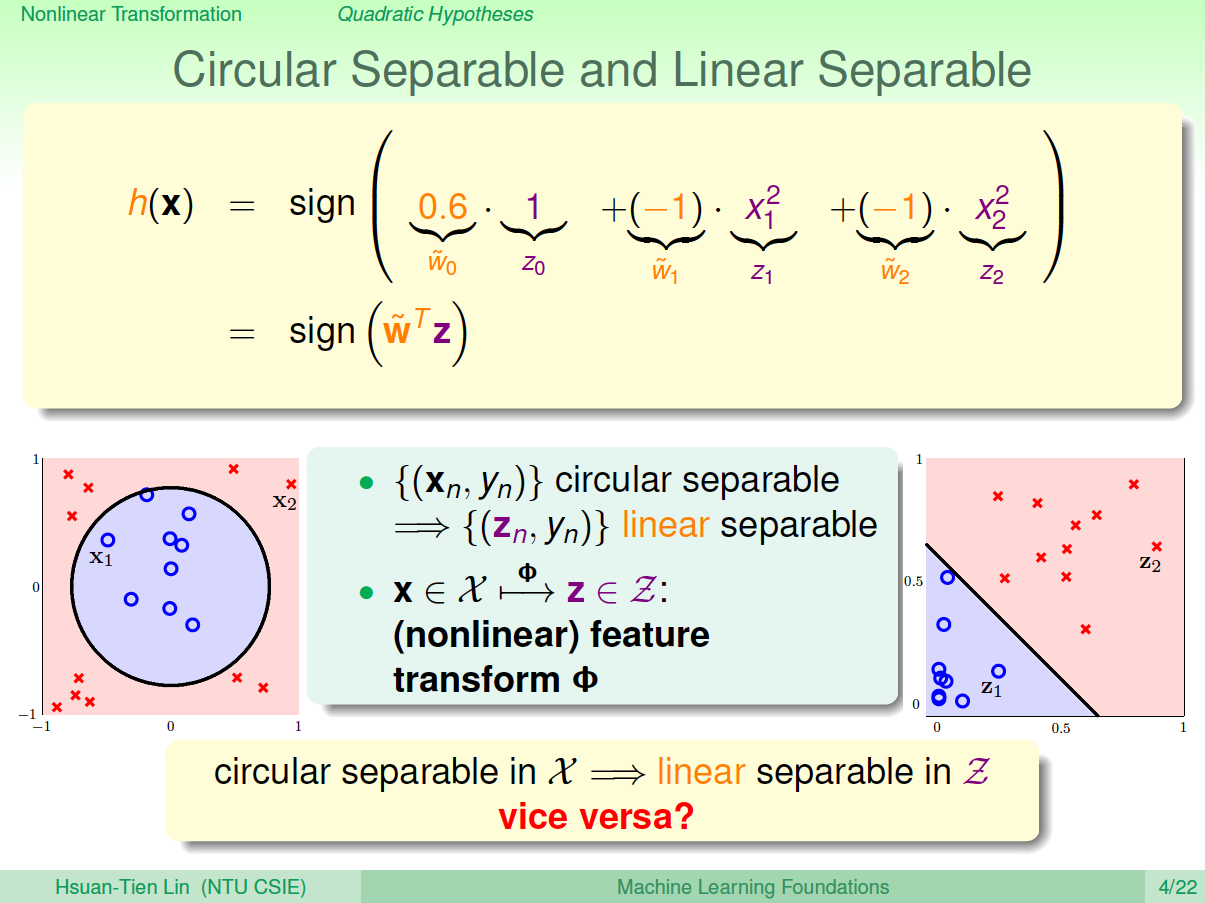
已知\(x\)域中圆形可分在\(z\)域中是线性可分的,那么反过来,如果在\(z\)域中线性可分,是否在\(x\)域中一定是圆形可分的呢?答案是否定的。由于权重向量\(w\)取值不同,\(x\)域中的hypothesis可能是圆形、椭圆、双曲线等等多种情况。

目前讨论的x域中的圆形都是圆心过原点的,对于圆心不过原点的一般情况, \(x_n\)到\(z_n\)映射公式包含的所有项为:\[\Psi_2(x)=(1,x_1,x_2,x^2_1,x_1x_2,x^2_2)\] 也就是说,对于二次hypothesis,它包含二次项、一次项和常数项\(1\),\(z\)域中每一条线对应\(x\)域中的某二次曲线的分类方式,也许是圆,也许是椭圆,也许是双曲线等等。那么\(z\)域中的hypothesis可以写成:
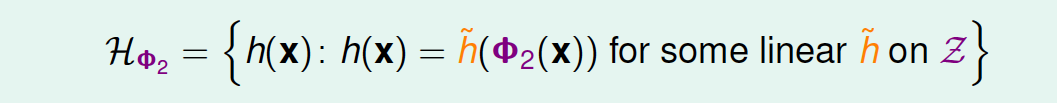
二、Nonlinear Transform
上一部分我们定义了什么了二次hypothesis,那么这部分将介绍如何设计一个好的二次hypothesis来达到良好的分类效果。那么目标就是在\(z\)域中设计一个最佳的分类线。

其实,做法很简单,利用映射变换的思想,通过映射关系,把\(x\)域中的最高阶二次的多项式转换为\(z\)域中的一次向量,也就是从quardratic hypothesis转换成了perceptrons问题。用\(z\)值代替\(x\)多项式,其中向量\(z\)的个数与\(x\)域中\(x\)多项式的个数一致(包含常数项)。这样就可以在\(z\)域中利用线性分类模型进行分类训练。训练好的线性模型之后,再将\(z\)替换为\(x\)的多项式就可以了。具体过程如下:
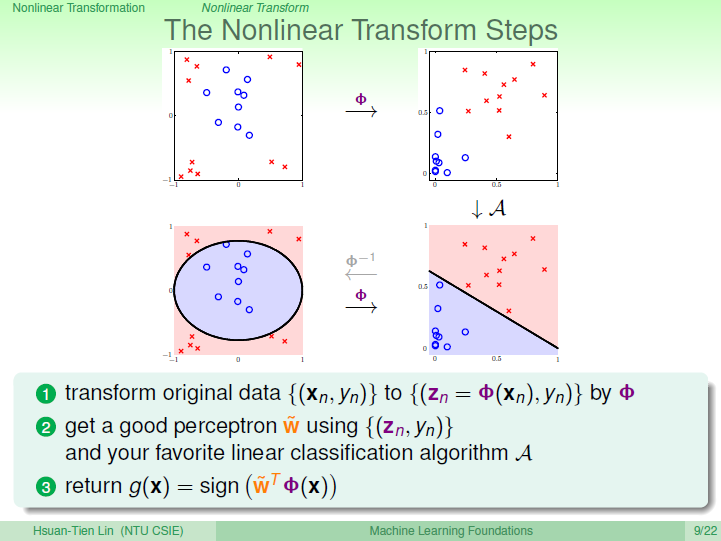
整个过程就是通过映射关系,换个空间去做线性分类,重点包括两个:
- 特征转换
- 训练线性模型
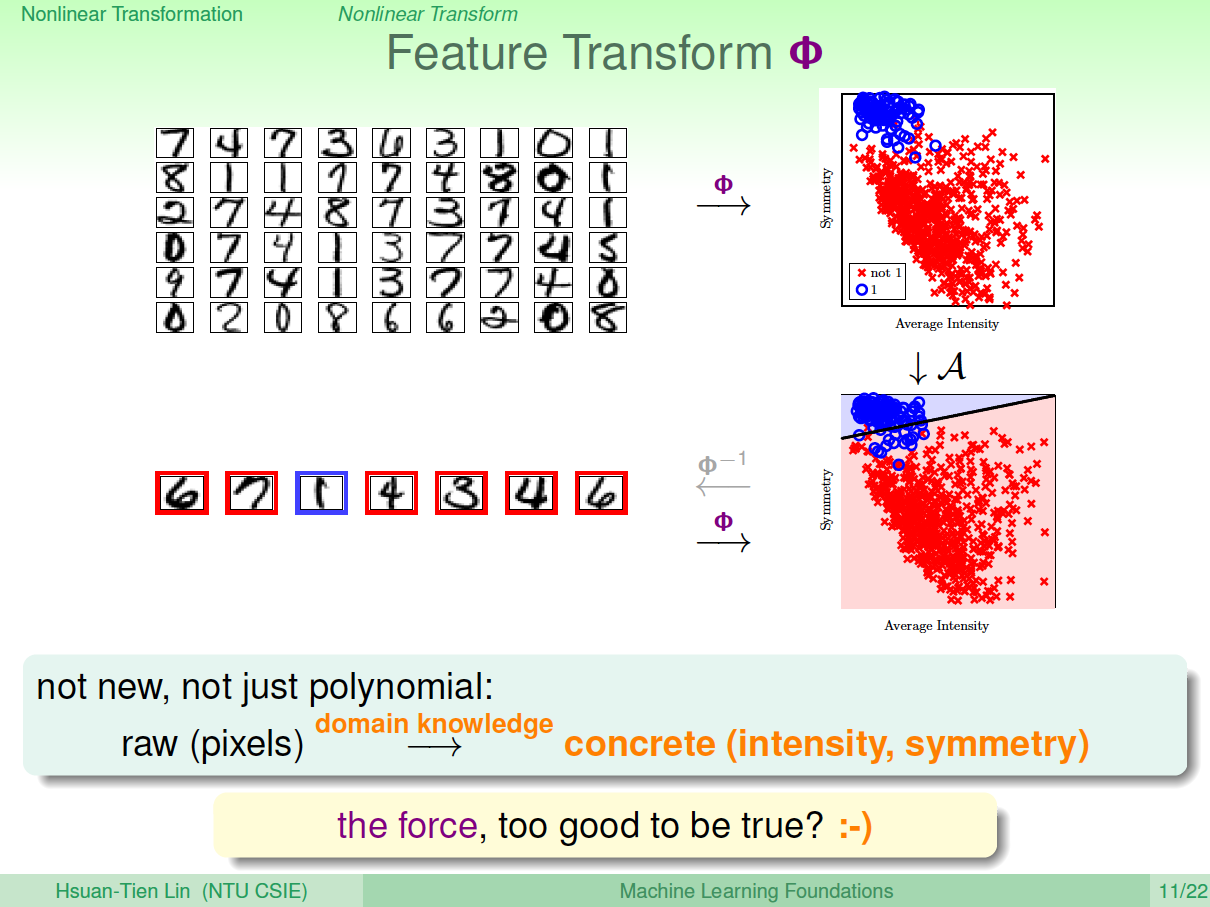
其实,我们以前处理机器学习问题的时候,已经做过类似的特征变换了。比如数字识别问题,我们从原始的像素值特征转换为一些实际的concrete特征,比如密度、对称性等等,这也用到了feature transform的思想。
三、Price of Nonlinear Transform
若\(x\)特征维度是\(d\)维的,也就是包含\(d\)个特征,那么二次多项式个数,即\(z\)域特征维度是:\[\tilde{d}=1+C^1_d+C^2_d+d=\frac{d(d+3)}{2}+1\]如果\(x\)特征维度是2维的,即\((x_1,x_2)\),那么它的二次多项式为\((1,x_1,x_2,x^2_1,x_1x_2,x^2_2)\),有6个。
现在,如果阶数更高,假设阶数为\(Q\),那么对于\(x\)特征维度是\(d\)维的,它的\(z\)域特征维度为:\[\tilde{d}=C^Q_{Q+d}=C^d_{Q+d}=O(Q^d)\]由上式可以看出,计算\(z\)域特征维度个数的时间复杂度是\(Q\)的\(d\)次方,随着\(Q\)和\(d\)的增大,计算量会变得很大。同时,空间复杂度也大。也就是说,这种特征变换的一个代价是计算的时间、空间复杂度都比较大。

另一方面,\(z\)域中特征个数随着\(Q\)和\(d\)增加变得很大,同时权重\(w\)也会增大,即自由度增加,VC Dimension增大。令\(z\)域中的特征维度是\(1+\tilde{d}\),则在\(z\)域中,任何\(\tilde{d}+2\)的输入都不能被shattered;同样,在\(x\)域中,任何的\(\tilde{d}+2\)输入也不能被shattered。\(\tilde{d}+1\)是VC Dimension的上界,如果\(\tilde{d}+1\)很大的时候,相应的VC Dimension就会很大。根据之前章节课程的讨论,VC Dimension过大,模型的泛化能力会比较差。

下面通过一个例子来解释为什么VC Dimension过大,会造成不好的分类效果:

上图中,左边是用直线进行线性分类,有部分点分类错误;右边是用四次曲线进行非线性分类,所有点都分类正确,那么哪一个分类效果好呢?单从平面上这些训练数据来看,四次曲线的分类效果更好,但是四次曲线模型很容易带来过拟合的问题,虽然它的\(E_{in}\)比较小,从泛化能力上来说,还是左边的分类器更好一些。也就是说VC Dimension过大会带来过拟合问题,\(\tilde{d}+1\)不能太大了。
那么如何选择合适的\(Q\),来保证不会出现过拟合问题,使模型的泛化能力强呢?一般情况下,为了尽量减少特征自由度,我们会根据训练样本的分布情况,人为地减少、省略一些项。但是,这种人为地删减特征会带来一些“自我分析”代价,虽然对训练样本分类效果好,但是对训练样本外的样本,不一定效果好。所以,一般情况下,还是要保存所有的多项式特征,避免对训练样本的人为选择。

四、Structured Hypothesis Sets
下面,我们讨论一下从\(x\)域到\(z\)域的多项式变换。首先,如果特征维度只有\(1\)维的话,那么变换多项式只有常数项:\[\phi_0(x)=(1)\]
如果特征维度是两维的,变换多项式包含了一维的\(\phi_0(x)\): \[\phi_1(x)=(\phi_0(x),x_1,x_2,...,x_d)\]
如果特征维度是三维的,变换多项式包含了二维的\(\phi_1(x)\): \[\phi_2(x)=(\phi_1(x),x^2_1,x_1x_2,...,x^2_d)\]
以此类推,如果特征维度是\(Q\)次,那么它的变换多项式为: \[\phi_Q(x)=(\phi_{Q-1}(x),x^Q_1,x^{Q-1}_1x_2,...,x^Q_d)\]
那么对于不同阶次构成的hypothesis有如下关系:\[H_{\phi_0} \subset H_{\phi_1} \subset H_{\phi_2} \subset \cdots \subset H_{\phi_Q} \]
我们把这种结构叫做Structured Hypothesis Sets:

那么对于这种Structured Hypothesis Sets,它们的VC Dimension满足下列关系:\[d_{VC}(H_0)\leq d_{VC}(H_1)\leq d_{VC}(H_2)\leq \cdots \leq d_{VC}(H_Q)\]
而它们的\(E_{in}\)满足下列关系:\[E_{in}(g_0)\geq E_{in}(g_1) \geq E_{in}(g_2) \geq \cdots \geq E_{in}(g_Q)\]

从上图中也可以看到,随着变换多项式的阶数增大,虽然\(E_{in}\)逐渐减小,但是model complexity会逐渐增大,造成\(E_{out}\)很大,所以阶数不能太高。
那么,如果选择的阶数很大,确实能使\(E_{in}\)接近于\(0\),但是泛化能力通常很差,我们把这种情况叫做tempting sin。所以,一般最合适的做法是先从低阶开始,如先选择一阶hypothesis,看看\(E_{in}\)是否很小,如果\(E_{in}\)足够小的话就选择一阶,如果\(E_{in}\)大的话,再逐渐增加阶数,直到满足要求为止。也就是说,尽量选择低阶的hypothes,这样才能得到较强的泛化能力。

五、总结
这节课主要介绍了非线性分类模型,通过非线性变换,将非线性模型映射到另一个空间,转换为线性模型,再来进行线性分类。本节课完整介绍了非线性变换的整体流程,以及非线性变换可能会带来的一些问题:时间复杂度和空间复杂度的增加。最后介绍了在要付出代价的情况下,使用非线性变换的最安全的做法,尽可能使用简单的模型,而不是模型越复杂越好。
机器学习基石12-Nonlinear Transformation的更多相关文章
- 机器学习基石笔记:12 Nonlinear Transformation
一.二次假设 实际上线性假设的模型复杂度是受到限制的, 需要高次假设打破这个限制. 假设数据不是线性可分的,但是可以被一个圆心在原点的圆分开, 需要我们重新设计基于该圆的PLA等算法吗? 不用, 只需 ...
- 12 Nonlinear Transformation
一.二次假设 实际上线性假设的复杂度是受到限制的, 需要高次假设打破这个限制 假设数据不是线性可分的,但是可以被一个圆心在原点的圆分开, 需要我们重新设计基于该圆的PLA等算法吗 不用, 只需要通过非 ...
- 机器学习基石 5 Training versus Testing
机器学习基石 5 Training versus Testing Recap and Preview 回顾一下机器学习的流程图: 机器学习可以理解为寻找到 \(g\),使得 \(g \approx f ...
- 机器学习基石 4 Feasibility of Learning
机器学习基石 4 Feasibility of Learning Learning is Impossible? 机器学习:通过现有的训练集 \(D\) 学习,得到预测函数 \(h(x)\) 使得它接 ...
- 机器学习基石 3 Types of Learning
机器学习基石 3 Types of Learning Learning with Different Output Space Learning with Different Data Label L ...
- 机器学习基石 2 Learning to Answer Yes/No
机器学习基石 2 Learning to Answer Yes/No Perceptron Hypothesis Set 对于一个线性可分的二分类问题,我们可以采用感知器 (Perceptron)这种 ...
- 机器学习基石 1 The Learning Problem
机器学习基石 1 The Learning Problem Introduction 什么是机器学习 机器学习是计算机通过数据和计算获得一定技巧的过程. 为什么需要机器学习 1 人无法获取数据或者数据 ...
- 機器學習基石(Machine Learning Foundations) 机器学习基石 课后习题链接汇总
大家好,我是Mac Jiang,非常高兴您能在百忙之中阅读我的博客!这个专题我主要讲的是Coursera-台湾大学-機器學習基石(Machine Learning Foundations)的课后习题解 ...
- ML笔记_机器学习基石01
1 定义 机器学习 (Machine Learning):improving some performance measure with experience computed from data ...
随机推荐
- mysql中将多行数据合并成一行数据
.1GROUP_CONCAT()中的值为你要合并的数据的字段名; SEPARATOR 函数是用来分隔这些要合并的数据的: ' '中是你要用哪个符号来分隔: 2.必须要用GROUP BY 语句来进行分组 ...
- Jdbc、Mybatis、Hibernate各自优缺点及区别
文章出处:Jdbc,Mybatis,Hibernate各自优缺点及区别 先比较下jdbc编程和hibernate编程各自的优缺点. 1.JDBC 我们平时使用jdbc进行编程,大致需要下面几个步骤: ...
- jexus上部署nuget私服vs访问403错误解决方式
因为vs去访问nuget项目的时候是以下面的方式去访问的 http://域名/nuget/Search()?$filter=IsLatestVersion&searchTerm=''& ...
- RabbitMQ之安装
RabbitMQ是一个消息代理.它的核心原理非常简单:接收和发送消息.你可以把它想像成一个邮局:你把信件放入邮箱,邮递员就会把信件投递到你的收件人处.在这个比喻中,RabbitMQ就扮演着邮箱.邮局以 ...
- PHP二维数组去重(指定键名)
本例对二维数组中某个指定键名进行去重,发现网上大多使用array_unique或是foreach遍历等方式去重,效果不佳且较为繁琐. 本文以二维数组去重为引,介绍array_column函数的三种用法 ...
- Java数据库学习之模糊查询(like )
Java数据库学习之模糊查询(like ): 第一种方式:直接在SQL语句中进行拼接,此时需要注意的是parm在SQL语句中需要用单引号拼接起来,注意前后单引号之间不能空格 String sql = ...
- LeetCode33—搜索旋转排序数组
方法一:先找到旋转点,然后根据目标值重新确定二分查找区域. 时间复杂度:用到两次二分查找,每次二分查找粗略的认为是O(logn),那么时间复杂度为2 * O(logn): 空间复杂度:O(1). in ...
- 使用Yii2的Web框架搭建微服务框架
方法 使用自己的Yii2镜像作为基础 使用Yii2的Web框架搭建,为了节省搭建Yii2框架的时间,直接使用现有的Yii2项目,删除了业务相关的逻辑类,将这个代码库作为搭建微服务框架的基础,本身已经积 ...
- js定时器 实现提交成功提示
应用场景: 用户评论后,在合适位置弹出“评论成功”,2秒钟后自动消失,提示用户评论成功. HTML: {#评论成功提示#} <div class="popup_con" st ...
- laravel 【error】MethodNotAllowedHttpException No message
Symfony \ Component \ HttpKernel \ Exception \ MethodNotAllowedHttpException No message 报错原因[原理]CSRF ...
