模型的偏差bias以及方差variance

1. 模型的偏差以及方差：

模型的偏差：是一个相对来说简单的概念：训练出来的模型在训练集上的准确度。

模型的方差：模型是随机变量。设样本容量为n的训练集为随机变量的集合(X1, X2, ..., Xn)，那么模型是以这些随机变量为输入的随机变量函数（其本身仍然是随机变量）：F(X1, X2, ..., Xn)。抽样的随机性带来了模型的随机性。

　　我们认为方差越大的模型越容易过拟合：假设有两个训练集A和B，经过A训练的模型Fa与经过B训练的模型Fb差异很大，这意味着Fa在类A的样本集合上有更好的性能，而Fb在类B的训练样本集合上有更好的性能，这样导致在不同的训练集样本的条件下，训练得到的模型的效果差异性很大，很不稳定，这便是模型的过拟合现象，而对于一些弱模型，它在不同的训练样本集上性能差异并不大，因此模型方差小，抗过拟合能力强，因此boosting算法就是基于弱模型来实现防止过拟合现象。

　　我们常说集成学习框架中的基模型是弱模型，通常来说弱模型是偏差高（在训练集上准确度低），方差小（防止过拟合能力强）的模型。但是，并不是所有集成学习框架中的基模型都是弱模型。bagging和stacking中的基模型为强模型（偏差低方差高），boosting中的基模型为弱模型。

　　在bagging和boosting框架中，通过计算基模型的期望和方差，我们可以得到模型整体的期望和方差。为了简化模型，我们假设基模型的权重、方差及两两间的相关系数相等。由于bagging和boosting的基模型都是线性组成的，那么有：

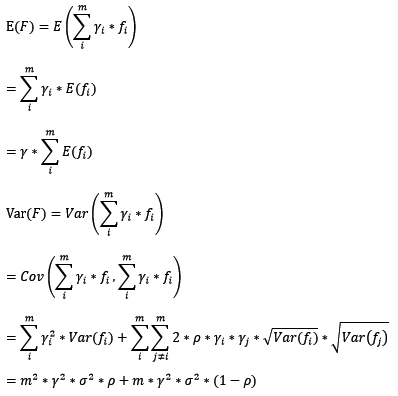
2. bagging的偏差和方差

　　对于bagging来说，每个基模型的权重等于1/m且期望近似相等（子训练集都是从原训练集中进行子抽样），故我们可以进一步化简得到：

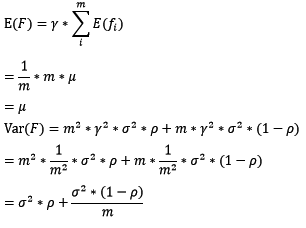
　　根据上式我们可以看到，整体模型的期望近似于基模型的期望，这也就意味着整体模型的偏差和基模型的偏差近似。同时，整体模型的方差小于等于基模型的方差（当相关性为1时取等号），随着基模型数（m）的增多，整体模型的方差减少，从而防止过拟合的能力增强，模型的准确度得到提高。但是，模型的准确度一定会无限逼近于1吗？并不一定，当基模型数增加到一定程度时，方差公式第二项的改变对整体方差的作用很小，防止过拟合的能力达到极限，这便是准确度的极限了。另外，在此我们还知道了为什么bagging中的基模型一定要为强模型，否则就会导致整体模型的偏差度低，即准确度低。

　　Random Forest是典型的基于bagging框架的模型，其在bagging的基础上，进一步降低了模型的方差。Random Fores中基模型是树模型，在树的内部节点分裂过程中，不再是将所有特征，而是随机抽样一部分特征纳入分裂的候选项。这样一来，基模型之间的相关性降低，从而在方差公式中，第一项显著减少，第二项稍微增加，整体方差仍是减少。

3. boosting的偏差和方差

　　对于boosting来说，基模型的训练集抽样是强相关的，那么模型的相关系数近似等于1，故我们也可以针对boosting化简公式为：

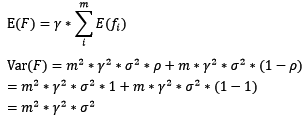
通过观察整体方差的表达式，我们容易发现，若基模型不是弱模型，其方差相对较大，这将导致整体模型的方差很大，即无法达到防止过拟合的效果。因此，boosting框架中的基模型必须为弱模型。

　　因为基模型为弱模型，导致了每个基模型的准确度都不是很高（因为其在训练集上的准确度不高）。随着基模型数的增多，整体模型的期望值增加，更接近真实值，因此，整体模型的准确度提高。但是准确度一定会无限逼近于1吗？仍然并不一定，因为训练过程中准确度的提高的主要功臣是整体模型在训练集上的准确度提高，而随着训练的进行，整体模型的方差变大，导致防止过拟合的能力变弱，最终导致了准确度反而有所下降。

　　基于boosting框架的Gradient Tree Boosting模型中基模型也为树模型，同Random Forrest，我们也可以对特征进行随机抽样来使基模型间的相关性降低，从而达到减少方差的效果。

4. 模型的独立性

　　衡量模型之间独立性：抽样的随机性决定了模型的随机性，如果两个模型的训练集抽样过程不独立，则两个模型则不独立，bagging中基模型的训练样本都是独立的随机抽样，但是基模型却不一定独立，因为我们讨论模型的随机性时，抽样是针对于样本的整体。而bagging中的抽样是针对于训练集（整体的子集），所以并不能称其为对整体的独立随机抽样。那么到底bagging中基模型的相关性体现在哪呢？总结下bagging的抽样为两个过程：

样本抽样：整体模型F(X1, X2, ..., Xn)中各输入随机变量（X1, X2, ..., Xn）对样本的抽样
子抽样：从整体模型F(X1, X2, ..., Xn)中随机抽取若干输入随机变量成为基模型的输入随机变量

　　假若在子抽样的过程中，两个基模型抽取的输入随机变量有一定的重合，那么这两个基模型对整体样本的抽样将不再独立，这时基模型之间便具有了相关性。